《1.1探索勾股定理》同步优生提升训练(附答案)2021-2022学年八年级数学北师大版上册(word版含答案)
文档属性
| 名称 | 《1.1探索勾股定理》同步优生提升训练(附答案)2021-2022学年八年级数学北师大版上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 538.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览


文档简介
2021年北师大版八年级数学上册《1.1探索勾股定理》同步优生提升训练(附答案)
1.如图所示,在△ABC中,AB=AC=5,BC=8.CD是AB边上的高线,则AD的长度为( )
A. B. C. D.
2.如图,点、、在正方形网络中的格点上,每个小正方形的边长为1,则网格上的三边中,,边长为无理数的边数有( )
A.0条 B.1条 C.2条 D.3条
3.点P在第三象限内,P到X轴的距离与到y轴的距离之比为,到原点的距离为,则点P的坐标为( )
A. B. C. D.
4.在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( )
A.14 B.42 C.32 D.42或32
5.如图,分别以直角三角形的三边为边长向外作等边三角形,面积分别记为S1、S2、S3,则S1、S2、S3之间的关系是( )
A.S12+S22=S32 B.S1+S2>S3 C.S1+S2<S3 D.S1+S2=S3
6.下列说法中,正确的是( )
A.直角三角形中,已知两边长为3和4,则第三边长为5
B.三角形是直角三角形,三角形的三边为a,b,c则满足a2-b2=c2
C.以三个连续自然数为三边长不可能构成直角三角形
D.△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形
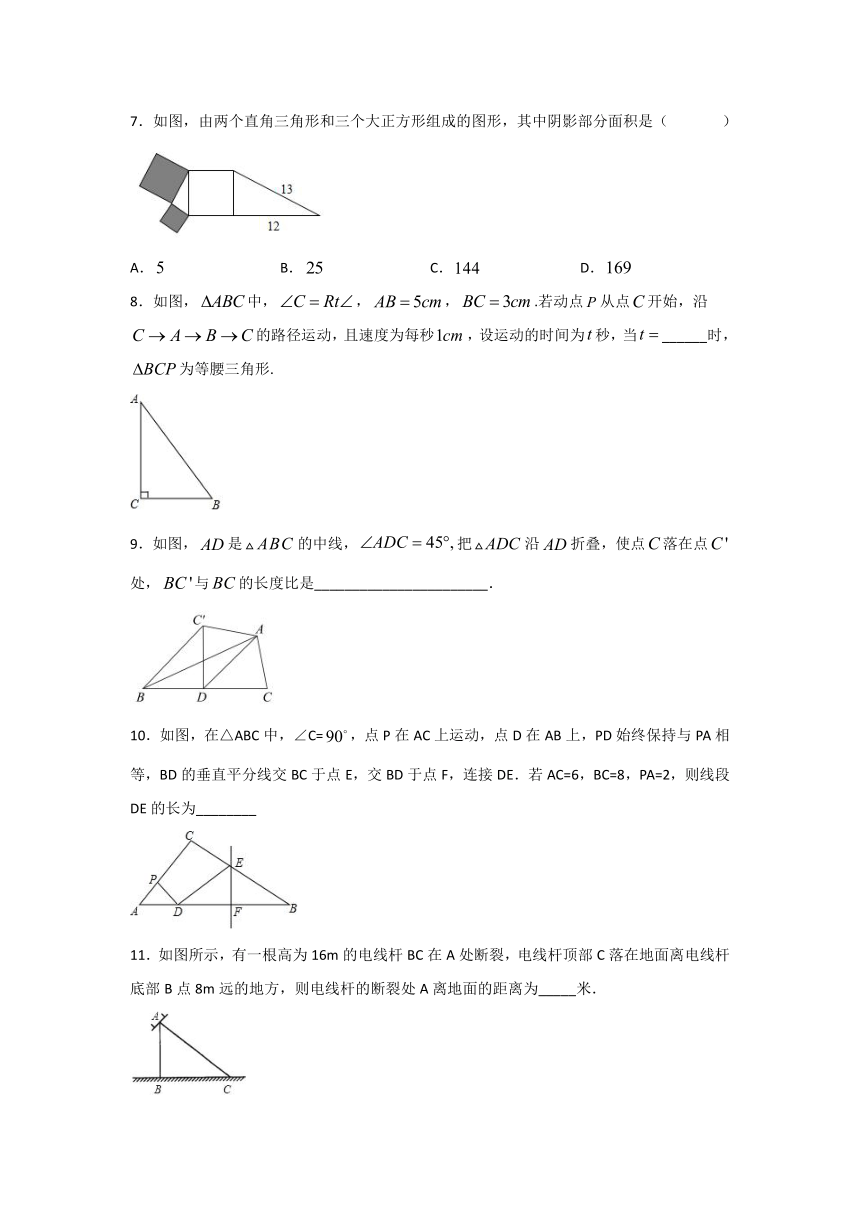
7.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A. B. C. D.
8.如图,中,,,.若动点从点开始,沿的路径运动,且速度为每秒,设运动的时间为秒,当______时,为等腰三角形.
9.如图,是的中线,把沿折叠,使点落在点处,与的长度比是_______________________.
10.如图,在△ABC中,∠C=,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.若AC=6,BC=8,PA=2,则线段DE的长为________
11.如图所示,有一根高为16m的电线杆BC在A处断裂,电线杆顶部C落在地面离电线杆底部B点8m远的地方,则电线杆的断裂处A离地面的距离为_____米.
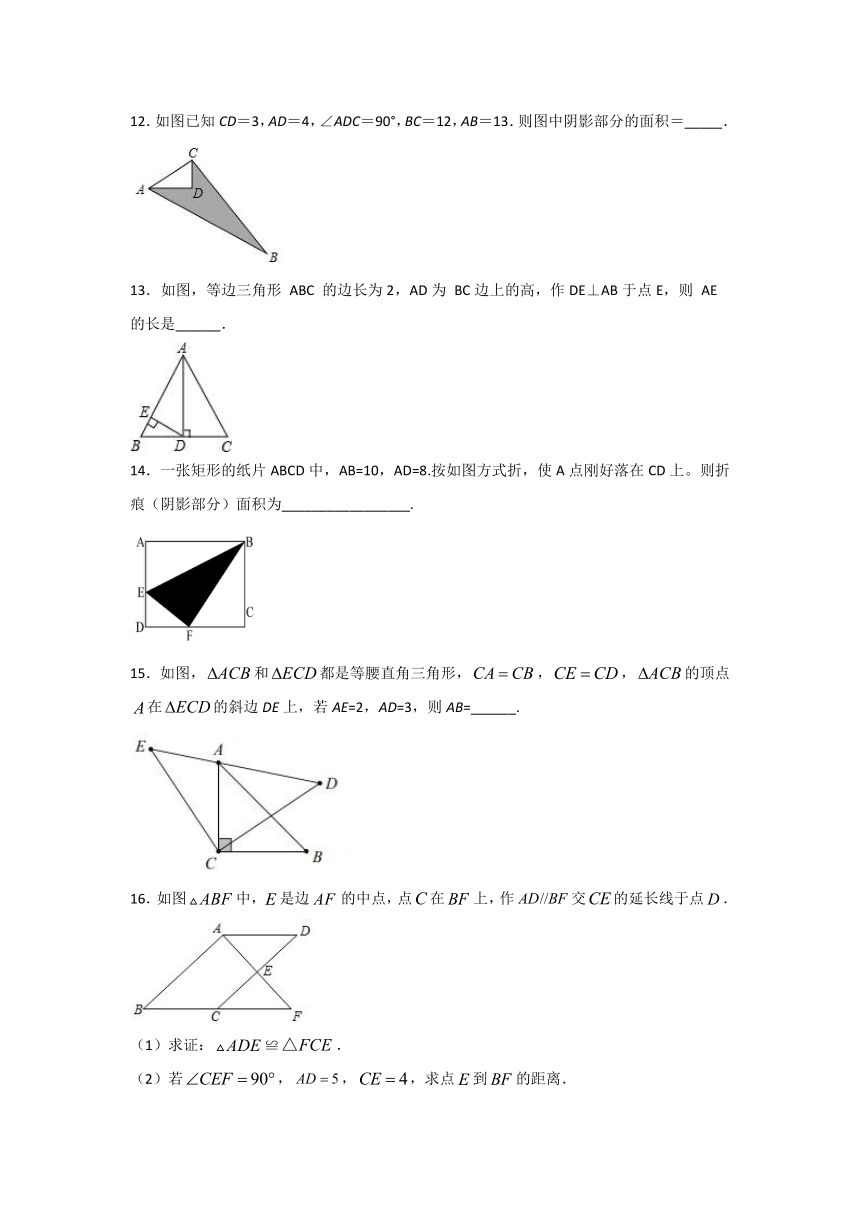
12.如图已知CD=3,AD=4,∠ADC=90°,BC=12,AB=13.则图中阴影部分的面积=_____.
13.如图,等边三角形 ABC 的边长为2,AD为 BC边上的高,作DE⊥AB于点E,则 AE的长是______.
14.一张矩形的纸片ABCD中,AB=10,AD=8.按如图方式折,使A点刚好落在CD上。则折痕(阴影部分)面积为_________________.
15.如图,和都是等腰直角三角形,,,的顶点在的斜边DE上,若AE=2,AD=3,则AB=______.
16.如图中,是边的中点,点在上,作交的延长线于点.
(1)求证:≌.
(2)若,,,求点到的距离.
17.如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.
18.如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
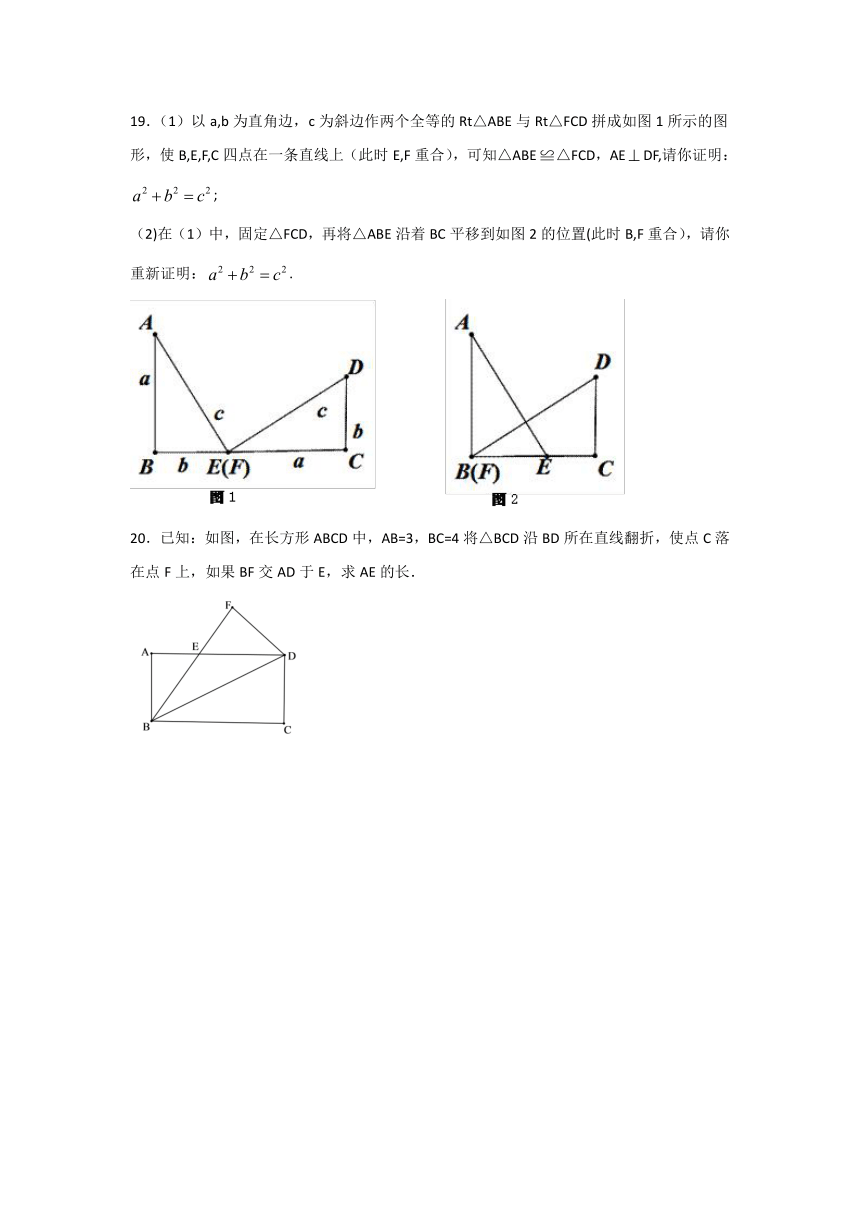
19.(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AEDF,请你证明:;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:.
20.已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.
参考答案
1 2 3 4 5 6 7
D C C D D D B
8.t=3秒或5.4秒或6秒或6.5秒
解:∵,,,
∴AC=4cm,
△BCP为等腰三角形时,分三种情况:①如果CP=CB,那么点P在AC上,CP=3cm,此时t=3÷1=3(秒);
如果CP=CB,点P在AB上,
作AB边上的高CE,
×AC×BC=×AB×CE,
则CE=2.4 cm,
由勾股定理得,EP==1.8 cm,
∴BP=3.6 cm,AP=1.4 cm,
∴t=(4+1.4)÷1=5.4(秒);
②如果BC=BP,那么点P在AB上,BP=3cm,CA+AP=4+5-3=6(cm),此时t=6÷1=6(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+AP=4+2.5=6.5(cm),
t=6.5÷1=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
9.
解:∵点D是BC的中点,设BD=CD=x,则BC=2x,
又∵∠ADC=45°,将ADC沿AD折叠,故,=x,
∴,是直角三角形,
根据勾股定理可得:,
∴,
故答案为:.
10.
解:∵PD=PA,
∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°?90°=90°,
∴DE⊥DP,
连接PE,
设DE=x,则EB=ED=x,CE=8?x,
∵∠C=∠PDE=90°,
∴PC2+CE2=PE2=PD2+DE2,
∴42+(8?x)2=22+x2,
解得:x=,
则DE=.
11.x=6.
解:设AB=x,则AC=16-x.
根据勾股定理,得x2+64=(16-x)2,
∴x2+64=x2-32x+256,
∴32x=192,
解之得:x=6.
12.24
解:由勾股定理可知:AC5.
又∵AC2+BC2=52+122=132=AB2,∴△ABC是直角三角形.
故所求面积=S△ABC﹣S△ACD5×123×4=30﹣6=24.
故答案为:24.
13.
解:∵△ABC是等边三角形,边长为 2,
∴BD=1,
∴AD==,
设ED的长为y,AE的长为x,则BE的长为2﹣x,
∵DE⊥AB,
∴x2+y2=3,(2﹣x)2+y2=1,
∴y2=3﹣x2,
∴(2﹣x)2+3﹣x2=1,
解得:x=,
则AE的长是.
故答案为:.
14.25
解:设,则
∵折叠
∴
∴
∴
∴DF=4
∴
解得
∴
故答案为25
15.
解:如图,连接BD,
∵△ACB和△ECD都是等腰直角三角形,
∴CE=CD,AC=BC,∠ECD=∠ACB=90°,
∴∠ACE=∠DCB,且CE=CD,AC=BC,
∴△ACE≌△BCD(SAS)
∴AE=BD=2,
∠CED=∠CDB=45°,
∵∠ADB=∠EDC+∠CDB
∴∠ADB=90°,
∴AB2=AD2+DB2= 32+22=13,
∴AB=,
故答案为.
16.解:(1)证明:∵,
∴.
∵是的中点,
∴.
在或中,,
∴≌(AAS).
(2)解:如图,过点作于.
∵≌(ASA),
∴.
∵,
∴.
∵,
∴.
17.解:(1)证明:∵∠CAB=90°.
∵BG⊥CF于点G,
∴∠BGF=∠CAB=90°.
∵∠GFB=∠CFA
∴∠ABG=∠ACF
(2)CG=AG+BG
在CG上截取CH=BG,连接AH,
∵△ABC是等腰直角三角形,
∴∠CAB=90°,AB=AC.
∵∠ABG=∠ACH.
∴△ABG≌△ACH,
∴AG=AH,∠GAB=∠HAC.
∴∠GAH=90°.
∴AG2+AH2=GH2.
∴GH=AG,
∴CG=CH+GH=AG+BG,
18.(1)4;(2)当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等;(3)当v=cm/s时.t=时,△PAE与△QBF全等.
解:(1)当AP=PC时,直线BP平分△ABC的面积.此时t=4.
故答案为4.
(2)假设可能相等.则有82+(6﹣t)2=62+(8﹣t)2,
解得t=0,不符合题意,
所以当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等.
(3)①当点Q在线段BC上时,
在Rt△AEP和Rt△BFQ中,
∵∠AEP=∠BFQ=90°,∠C=90°,
∴∠A+∠B=90°,∠B+∠BQF=90°,
∴∠A=∠BQF,
∴当PA=BQ时,△AEP≌△FQB,
∴当v=1cm/s时,0<t≤6时,△PAE与△QBF全等.
②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等.设此时PA=PB=x,
在Rt△PBC中,∵PB2=PC2+BC2,
∴x2=(8﹣x)2+62,
∵当P,Q在AC边上相遇,可得
解得
∴当v=cm/s时.t=时,△PAE与△QBF全等.
19.解:(1)连接AD,如图1所示:
则四边形ABCD是直角梯形,
∴四边形ABCD的面积= (a+b)(a+b)=12(a+b)2,
∵四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,
即 (a+b)2=ab×2+c2,
化简得:(a+b)2=2ab+c2,
∴a2+b2=c2;
(2)连接AD、DE,如图2所示:
则四边形ABCD的面积=四边形ABED的面积+△DCE的面积,
即(a+b)×a=c2+b(a?b),
化简得:ab+a2=c2+ab?b2,
∴a2+b2=c2.
20.解:∵FD=DC=AB=3
在△ABE和△FDE中
∴△ABE≌△FDE(AAS)
∴AE=FE,BE=DE
在Rt△ABE中,由勾股定理得
BE2=AE2+32,设AE=x,则(4-x)2=x2+32,
解之得x=,
∴AE=
1.如图所示,在△ABC中,AB=AC=5,BC=8.CD是AB边上的高线,则AD的长度为( )
A. B. C. D.
2.如图,点、、在正方形网络中的格点上,每个小正方形的边长为1,则网格上的三边中,,边长为无理数的边数有( )
A.0条 B.1条 C.2条 D.3条
3.点P在第三象限内,P到X轴的距离与到y轴的距离之比为,到原点的距离为,则点P的坐标为( )
A. B. C. D.
4.在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( )
A.14 B.42 C.32 D.42或32
5.如图,分别以直角三角形的三边为边长向外作等边三角形,面积分别记为S1、S2、S3,则S1、S2、S3之间的关系是( )
A.S12+S22=S32 B.S1+S2>S3 C.S1+S2<S3 D.S1+S2=S3
6.下列说法中,正确的是( )
A.直角三角形中,已知两边长为3和4,则第三边长为5
B.三角形是直角三角形,三角形的三边为a,b,c则满足a2-b2=c2
C.以三个连续自然数为三边长不可能构成直角三角形
D.△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形
7.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A. B. C. D.
8.如图,中,,,.若动点从点开始,沿的路径运动,且速度为每秒,设运动的时间为秒,当______时,为等腰三角形.
9.如图,是的中线,把沿折叠,使点落在点处,与的长度比是_______________________.
10.如图,在△ABC中,∠C=,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.若AC=6,BC=8,PA=2,则线段DE的长为________
11.如图所示,有一根高为16m的电线杆BC在A处断裂,电线杆顶部C落在地面离电线杆底部B点8m远的地方,则电线杆的断裂处A离地面的距离为_____米.
12.如图已知CD=3,AD=4,∠ADC=90°,BC=12,AB=13.则图中阴影部分的面积=_____.
13.如图,等边三角形 ABC 的边长为2,AD为 BC边上的高,作DE⊥AB于点E,则 AE的长是______.
14.一张矩形的纸片ABCD中,AB=10,AD=8.按如图方式折,使A点刚好落在CD上。则折痕(阴影部分)面积为_________________.
15.如图,和都是等腰直角三角形,,,的顶点在的斜边DE上,若AE=2,AD=3,则AB=______.
16.如图中,是边的中点,点在上,作交的延长线于点.
(1)求证:≌.
(2)若,,,求点到的距离.
17.如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.
18.如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
19.(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AEDF,请你证明:;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:.
20.已知:如图,在长方形ABCD中,AB=3,BC=4将△BCD沿BD所在直线翻折,使点C落在点F上,如果BF交AD于E,求AE的长.
参考答案
1 2 3 4 5 6 7
D C C D D D B
8.t=3秒或5.4秒或6秒或6.5秒
解:∵,,,
∴AC=4cm,
△BCP为等腰三角形时,分三种情况:①如果CP=CB,那么点P在AC上,CP=3cm,此时t=3÷1=3(秒);
如果CP=CB,点P在AB上,
作AB边上的高CE,
×AC×BC=×AB×CE,
则CE=2.4 cm,
由勾股定理得,EP==1.8 cm,
∴BP=3.6 cm,AP=1.4 cm,
∴t=(4+1.4)÷1=5.4(秒);
②如果BC=BP,那么点P在AB上,BP=3cm,CA+AP=4+5-3=6(cm),此时t=6÷1=6(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+AP=4+2.5=6.5(cm),
t=6.5÷1=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
9.
解:∵点D是BC的中点,设BD=CD=x,则BC=2x,
又∵∠ADC=45°,将ADC沿AD折叠,故,=x,
∴,是直角三角形,
根据勾股定理可得:,
∴,
故答案为:.
10.
解:∵PD=PA,
∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°?90°=90°,
∴DE⊥DP,
连接PE,
设DE=x,则EB=ED=x,CE=8?x,
∵∠C=∠PDE=90°,
∴PC2+CE2=PE2=PD2+DE2,
∴42+(8?x)2=22+x2,
解得:x=,
则DE=.
11.x=6.
解:设AB=x,则AC=16-x.
根据勾股定理,得x2+64=(16-x)2,
∴x2+64=x2-32x+256,
∴32x=192,
解之得:x=6.
12.24
解:由勾股定理可知:AC5.
又∵AC2+BC2=52+122=132=AB2,∴△ABC是直角三角形.
故所求面积=S△ABC﹣S△ACD5×123×4=30﹣6=24.
故答案为:24.
13.
解:∵△ABC是等边三角形,边长为 2,
∴BD=1,
∴AD==,
设ED的长为y,AE的长为x,则BE的长为2﹣x,
∵DE⊥AB,
∴x2+y2=3,(2﹣x)2+y2=1,
∴y2=3﹣x2,
∴(2﹣x)2+3﹣x2=1,
解得:x=,
则AE的长是.
故答案为:.
14.25
解:设,则
∵折叠
∴
∴
∴
∴DF=4
∴
解得
∴
故答案为25
15.
解:如图,连接BD,
∵△ACB和△ECD都是等腰直角三角形,
∴CE=CD,AC=BC,∠ECD=∠ACB=90°,
∴∠ACE=∠DCB,且CE=CD,AC=BC,
∴△ACE≌△BCD(SAS)
∴AE=BD=2,
∠CED=∠CDB=45°,
∵∠ADB=∠EDC+∠CDB
∴∠ADB=90°,
∴AB2=AD2+DB2= 32+22=13,
∴AB=,
故答案为.
16.解:(1)证明:∵,
∴.
∵是的中点,
∴.
在或中,,
∴≌(AAS).
(2)解:如图,过点作于.
∵≌(ASA),
∴.
∵,
∴.
∵,
∴.
17.解:(1)证明:∵∠CAB=90°.
∵BG⊥CF于点G,
∴∠BGF=∠CAB=90°.
∵∠GFB=∠CFA
∴∠ABG=∠ACF
(2)CG=AG+BG
在CG上截取CH=BG,连接AH,
∵△ABC是等腰直角三角形,
∴∠CAB=90°,AB=AC.
∵∠ABG=∠ACH.
∴△ABG≌△ACH,
∴AG=AH,∠GAB=∠HAC.
∴∠GAH=90°.
∴AG2+AH2=GH2.
∴GH=AG,
∴CG=CH+GH=AG+BG,
18.(1)4;(2)当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等;(3)当v=cm/s时.t=时,△PAE与△QBF全等.
解:(1)当AP=PC时,直线BP平分△ABC的面积.此时t=4.
故答案为4.
(2)假设可能相等.则有82+(6﹣t)2=62+(8﹣t)2,
解得t=0,不符合题意,
所以当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等.
(3)①当点Q在线段BC上时,
在Rt△AEP和Rt△BFQ中,
∵∠AEP=∠BFQ=90°,∠C=90°,
∴∠A+∠B=90°,∠B+∠BQF=90°,
∴∠A=∠BQF,
∴当PA=BQ时,△AEP≌△FQB,
∴当v=1cm/s时,0<t≤6时,△PAE与△QBF全等.
②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等.设此时PA=PB=x,
在Rt△PBC中,∵PB2=PC2+BC2,
∴x2=(8﹣x)2+62,
∵当P,Q在AC边上相遇,可得
解得
∴当v=cm/s时.t=时,△PAE与△QBF全等.
19.解:(1)连接AD,如图1所示:
则四边形ABCD是直角梯形,
∴四边形ABCD的面积= (a+b)(a+b)=12(a+b)2,
∵四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,
即 (a+b)2=ab×2+c2,
化简得:(a+b)2=2ab+c2,
∴a2+b2=c2;
(2)连接AD、DE,如图2所示:
则四边形ABCD的面积=四边形ABED的面积+△DCE的面积,
即(a+b)×a=c2+b(a?b),
化简得:ab+a2=c2+ab?b2,
∴a2+b2=c2.
20.解:∵FD=DC=AB=3
在△ABE和△FDE中
∴△ABE≌△FDE(AAS)
∴AE=FE,BE=DE
在Rt△ABE中,由勾股定理得
BE2=AE2+32,设AE=x,则(4-x)2=x2+32,
解之得x=,
∴AE=
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
