1.3勾股定理的应用 提高练习 2021-2022学年北师大版数学八年级上册(word含解析)
文档属性
| 名称 | 1.3勾股定理的应用 提高练习 2021-2022学年北师大版数学八年级上册(word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 480.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 19:42:49 | ||
图片预览




文档简介
1.3勾股定理的应用
提高练习
一、单选题
1.如图,在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出1,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5,由此可计算出学校旗杆的高度是(
)
A.8m
B.10m
C.12m
D.15m
2.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是(
)
A.12≤a≤13
B.12≤a≤15
C.5≤a≤12
D.5≤a≤13
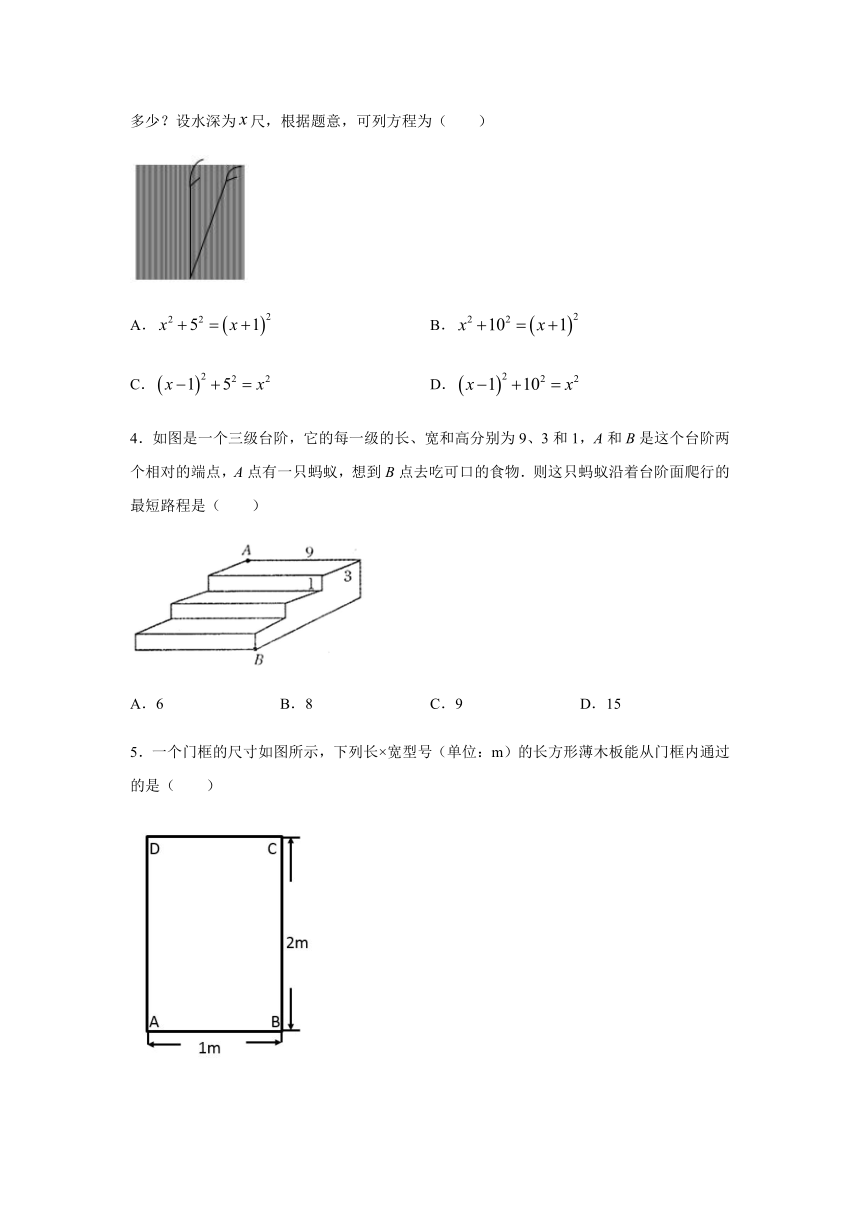
3.我国古代数学著作《九章算术》记载了一道有趣的问题,原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设水深为尺,根据题意,可列方程为(
)
A.
B.
C.
D.
4.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是(
)
A.6
B.8
C.9
D.15
5.一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框内通过的是(
)
A.
B.
C.
D.
6.一帆船先向正西航行24千米,然后向正南航行10千米,这时它离出发点有(
)千米.
A.26
B.18
C.13
D.32
7.如图,一木杆在离地某处断裂,木杆顶部落在离木杆底部8米处,断落的木杆与地面形成角,则木杆原来的长度是( )
A.8米
B.米
C.16米
D.24米
8.如图,一棵大树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为(
)
A.6米
B.8米
C.10米
D.12米
9.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走(
)
A.20
B.24
C.25
D.26
10.如图所示,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在外面的长为hcm,则h的取值范围是( )
A.0<h≤11
B.11≤h≤12
C.h≥12
D.0<h≤12
11.如图,已知ABCD是长方形纸片,,在CD上存在一点E,沿直线AE将折叠,D恰好落在BC边上的点F处,且,则的面积是(
).
A.
B.
C.
D.
12.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是(
)
A.12
B.13
C.15
D.24
13.一根竹竿插到水池中离岸边1.5m远的水底,竹竿高出水面0.5m,若把竹竿的顶端拉向岸边,则竿顶刚好接触到岸边,并且和水面一样高,问水池的深度为( )
A.2m
B.2.5cm
C.2.25m
D.3m
14.用梯子登上20m高的建筑物,为了安全要使梯子的底面距离建筑物15m,至少需要(
)m长的梯子.
A.20
B.25
C.15
D.5
15.学习勾股定理后,老师布置的课后作业为“利用绳子(绳子足够长)和卷尺,测量学校教学楼的高度”,某数学兴趣小组的做法如下:①将绳子上端固定在教学楼顶部,绳子自由下垂,再垂直向外拉到离教学楼底部3m远处,在绳子与地面的交点处将绳子打结;②将绳子继续往外拉,使打结处离教学楼的距离为6m,此时测得绳结离地面的高度为
1m,则学校教学楼的高度为( )
A.11
m
B.13
m
C.14
m
D.15
m
二、填空题
16.我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为________尺.
17.如图,台阶阶梯每一层高,宽,长.一只蚂蚁从点爬到点,最短路程是____________.
18.如图,客船以24海里/时的速度从港口向东北方向航行,货船以18海里/时的速度同时从港口向东南方向航行,则1小时后两船相距______海里.
19.《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深________尺.
20.东汉《九章算术》中,“折竹抵底”问题,意思是:如图所示一根竹子,原高10尺,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少?_____.
三、解答题
21.一架云梯AB斜靠在墙上,梯子顶端距墙脚的距离AC=24米,梯子底端距墙脚的距离BC=7米.
(1)
求梯子的长度.
(2)
如果梯子的顶端下滑了4米,那么梯子的底端在水平方向也滑动4米吗?
为什么?
22.如图,花果山上有两只猴子在一棵树上的点B处,且,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树处的A处,另一只猴子乙先爬到项D处后再沿缆绳滑到A处.己知两只猴子所经过的路程相等,设为.求这棵树高有多少米?
23.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于种种原因,由C到A的路现在已经不通了,某村为方便村民取水决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是不是从村庄C到河边的最近路,请通过计算加以说明;
(2)求原来的路线AC的长.
24.如图,一艘轮船从小岛处出发,向正北方向以每小时20海里的速度行驶了1.5小时到达处执行任务,再向正东方向以相同的速度行驶了2小时到达处继续执行任务,然后以相同的速度直接从处返回处轮船返回时比出去时节省了多少时间?(不含执行任务时间)
25.某条道路限速如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,小汽车到达B处,此时测得小汽车与车速测检测仪间的距离为,这辆小汽车超速了吗?
参考答案
1.C
设旗杆的长度为xm,则绳子的长度为:(x+1)m,如图,
在Rt△ABC中,由勾股定理得:x2+52=(x+1)2,
解得:x=12,
∴旗杆的高度为12m.
故选:C.
2.A
解:由题意可得:
a的最小长度为饮料罐的高,即为12,
当吸管斜放时,如图,此时a的长度最大,即为AB,
∵下底面半径是5,
∴AB==13,
∴a的取值范围是12≤a≤13,
故选A
3.A
解:设水深为尺,则芦苇长x+1尺,由题意得:,
,
故选:A.
4.D
解:如图,将台阶展开,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
故选:D.
5.A
门框的对角线长为米.
∵米.
∴只有A选项的薄木板的宽小于,即只有A选项的薄木板可以通过.
故选:A.
6.A
解:如图,根据题意得:△ABC是直角三角形,
∵∠B=90°,AB=24km,BC=10km,
根据勾股定理得AC2=AB2+BC2,
∴AC2=242+102,
∴AC=26km.
故选:A.
7.B
如图,根据题意可知为等腰直角三角形,且米,.
∴米.
∴在中,米
.
故木杆原来的长度为米.
故选:B.
8.D
如图所示,
由题可知:,,
∴,
∴米;
故答案选D.
9.D
展开如图得新矩形,连接AC,则其长度至少增加2MN,宽度不变,由此可得:
,
根据勾股定理有:
故选D.
10.B
解:当筷子与杯底垂直时h最大,h最大=24﹣12=12cm.
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:
此时,AB===13cm,
∴h=24﹣13=11cm.
∴h的取值范围是11cm≤h≤12cm.
故选:B.
11.B
解:ABCD是长方形纸片,
∴AB=CD=3,
,
∴,
∴BF=4,
∴AF=,
∴AF=AD=BC=5,CF=1,
设DE为x,EF=DE=x,EC=3-x,
x2=(3-x)2+1,
解得,x=
,
∴,
故选:B.
12.A
设旗杆的高度为m,则ACm,AB=m,BC=5m,
在中,
解得:
故选:A.
13.A
【分析】
设水池的深度BC=xm,则AB=(0.5+x)m,根据勾股定理列出方程,进而即可求解.
【详解】
解:在直角△ABC中,AC=1.5m.AB﹣BC=0.5m.
设水池的深度BC=xm,则AB=(0.5+x)m.
根据勾股定理得出:
∵AC2+BC2=AB2,
∴1.52+x2=(x+0.5)2,
解得:x=2.
故选:A.
14.B
如图所示:
∵AC=20m,BC=15m,
∴在Rt△ABC中,AB=m,
故选:B.
15.C
如图,
设学校教学楼的高度为,则,,,
左图,根据勾股定理得,绳长的平方,
右图,根据勾股定理得,绳长的平方,
∴,
解得:.
故选:C.
16.14.5
解:设秋千的绳索长为x尺,
由题意知:OC=x-(5-1)=(x-4)尺,CP′=10尺,OP′=x尺,
在Rt△OCP′中,由勾股定理得:
(x-4)?+10?=x?,
解得:x=14.5,
故答案为:14.5.
17.
如图所示,
∵楼梯的每一级的高宽长分别为20cm,宽40cm,长50cm,
∴(cm)
即蚂蚁从点A沿着台阶面爬行到点B的最短路程是130cm.
故答案为:130cm.
18.30
解:∵客船以24海里/时的速度从港口
A
向东北方向航行,
货船以18海里/时的速度同时从港口
A
向东南方向航行,
∴客船与货船方向的夹角为,
且客船行驶1小时的距离为24海里,货船行驶1小时的距离为18海里,
故两船1小时后的距离为海里,
故答案为:30.
19.12
解:依题意画出图形,设芦苇长AB=AB'=x尺,则水深AC=(x?1)尺,
因为B'E=10尺,所以B'C=5尺
在Rt△AB'C中,52+(x?1)2=x2,
解得:x=13,
即水深12尺,
故答案为:12
20.4.2尺.
解:如图所示:
由题意得:∠AOB=90°,
设折断处离地面的高度OA是x尺,
由勾股定理得:x2+42=(10﹣x)2,
解得:x=4.2,
即:折断后的竹子高度OA为4.2尺.
故答案为:4.2尺.
21.解:(1)由题意可得:
AC=24米,BC=7米,∠ACB=90°,
∴AB==25米,
∴梯子的长度为25米;
(2)如图,在Rt△CDE中,
∵CD=AC-4=24-4=20米,DE=25米,
∴CE==15米,
∴BE=CE-BC=15-7=8(米).
答:梯子底部在水平方向滑动了8米.
22.解:设BD为x米,且存在BD+DA=BC+CA,
即BD+DA=15,DA=15-x,
∵∠C=90°,
∴AD2=AC2+DC2,
∴(15-x)2=(x+5)2+102,
∴x=2.5,
∴CD=5+2.5=7.5,
答:树高7.5米.
23.(1)∵,即,
∴Rt△CHB是直角三角形,即CH⊥BH,
∴CH是从村庄C到河边的最近路(点到直线的距离中,垂线段最短);
(2)设AC=AB=x,则AH=x-1.8,
∵在Rt△ACH,
∴,即
,解得x=2.5,
∴原来的路线AC的长为2.5米.
24.
(海里),
(海里),
再Rt△ABC中,∠ABC=90°,
由勾股定理得:(海里),
∴返回所用时间为:小时,
出去所用时间为:小时,
∴则返回时比出去时节省的时间为:小时.
答:返回时比出去时节省了1小时.
25.解:在中,
米
,
,
所以小汽车超速了.
提高练习
一、单选题
1.如图,在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出1,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5,由此可计算出学校旗杆的高度是(
)
A.8m
B.10m
C.12m
D.15m
2.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是(
)
A.12≤a≤13
B.12≤a≤15
C.5≤a≤12
D.5≤a≤13
3.我国古代数学著作《九章算术》记载了一道有趣的问题,原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设水深为尺,根据题意,可列方程为(
)
A.
B.
C.
D.
4.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是(
)
A.6
B.8
C.9
D.15
5.一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框内通过的是(
)
A.
B.
C.
D.
6.一帆船先向正西航行24千米,然后向正南航行10千米,这时它离出发点有(
)千米.
A.26
B.18
C.13
D.32
7.如图,一木杆在离地某处断裂,木杆顶部落在离木杆底部8米处,断落的木杆与地面形成角,则木杆原来的长度是( )
A.8米
B.米
C.16米
D.24米
8.如图,一棵大树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为(
)
A.6米
B.8米
C.10米
D.12米
9.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走(
)
A.20
B.24
C.25
D.26
10.如图所示,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在外面的长为hcm,则h的取值范围是( )
A.0<h≤11
B.11≤h≤12
C.h≥12
D.0<h≤12
11.如图,已知ABCD是长方形纸片,,在CD上存在一点E,沿直线AE将折叠,D恰好落在BC边上的点F处,且,则的面积是(
).
A.
B.
C.
D.
12.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是(
)
A.12
B.13
C.15
D.24
13.一根竹竿插到水池中离岸边1.5m远的水底,竹竿高出水面0.5m,若把竹竿的顶端拉向岸边,则竿顶刚好接触到岸边,并且和水面一样高,问水池的深度为( )
A.2m
B.2.5cm
C.2.25m
D.3m
14.用梯子登上20m高的建筑物,为了安全要使梯子的底面距离建筑物15m,至少需要(
)m长的梯子.
A.20
B.25
C.15
D.5
15.学习勾股定理后,老师布置的课后作业为“利用绳子(绳子足够长)和卷尺,测量学校教学楼的高度”,某数学兴趣小组的做法如下:①将绳子上端固定在教学楼顶部,绳子自由下垂,再垂直向外拉到离教学楼底部3m远处,在绳子与地面的交点处将绳子打结;②将绳子继续往外拉,使打结处离教学楼的距离为6m,此时测得绳结离地面的高度为
1m,则学校教学楼的高度为( )
A.11
m
B.13
m
C.14
m
D.15
m
二、填空题
16.我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为________尺.
17.如图,台阶阶梯每一层高,宽,长.一只蚂蚁从点爬到点,最短路程是____________.
18.如图,客船以24海里/时的速度从港口向东北方向航行,货船以18海里/时的速度同时从港口向东南方向航行,则1小时后两船相距______海里.
19.《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深________尺.
20.东汉《九章算术》中,“折竹抵底”问题,意思是:如图所示一根竹子,原高10尺,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少?_____.
三、解答题
21.一架云梯AB斜靠在墙上,梯子顶端距墙脚的距离AC=24米,梯子底端距墙脚的距离BC=7米.
(1)
求梯子的长度.
(2)
如果梯子的顶端下滑了4米,那么梯子的底端在水平方向也滑动4米吗?
为什么?
22.如图,花果山上有两只猴子在一棵树上的点B处,且,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树处的A处,另一只猴子乙先爬到项D处后再沿缆绳滑到A处.己知两只猴子所经过的路程相等,设为.求这棵树高有多少米?
23.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于种种原因,由C到A的路现在已经不通了,某村为方便村民取水决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是不是从村庄C到河边的最近路,请通过计算加以说明;
(2)求原来的路线AC的长.
24.如图,一艘轮船从小岛处出发,向正北方向以每小时20海里的速度行驶了1.5小时到达处执行任务,再向正东方向以相同的速度行驶了2小时到达处继续执行任务,然后以相同的速度直接从处返回处轮船返回时比出去时节省了多少时间?(不含执行任务时间)
25.某条道路限速如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,小汽车到达B处,此时测得小汽车与车速测检测仪间的距离为,这辆小汽车超速了吗?
参考答案
1.C
设旗杆的长度为xm,则绳子的长度为:(x+1)m,如图,
在Rt△ABC中,由勾股定理得:x2+52=(x+1)2,
解得:x=12,
∴旗杆的高度为12m.
故选:C.
2.A
解:由题意可得:
a的最小长度为饮料罐的高,即为12,
当吸管斜放时,如图,此时a的长度最大,即为AB,
∵下底面半径是5,
∴AB==13,
∴a的取值范围是12≤a≤13,
故选A
3.A
解:设水深为尺,则芦苇长x+1尺,由题意得:,
,
故选:A.
4.D
解:如图,将台阶展开,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
故选:D.
5.A
门框的对角线长为米.
∵米.
∴只有A选项的薄木板的宽小于,即只有A选项的薄木板可以通过.
故选:A.
6.A
解:如图,根据题意得:△ABC是直角三角形,
∵∠B=90°,AB=24km,BC=10km,
根据勾股定理得AC2=AB2+BC2,
∴AC2=242+102,
∴AC=26km.
故选:A.
7.B
如图,根据题意可知为等腰直角三角形,且米,.
∴米.
∴在中,米
.
故木杆原来的长度为米.
故选:B.
8.D
如图所示,
由题可知:,,
∴,
∴米;
故答案选D.
9.D
展开如图得新矩形,连接AC,则其长度至少增加2MN,宽度不变,由此可得:
,
根据勾股定理有:
故选D.
10.B
解:当筷子与杯底垂直时h最大,h最大=24﹣12=12cm.
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:
此时,AB===13cm,
∴h=24﹣13=11cm.
∴h的取值范围是11cm≤h≤12cm.
故选:B.
11.B
解:ABCD是长方形纸片,
∴AB=CD=3,
,
∴,
∴BF=4,
∴AF=,
∴AF=AD=BC=5,CF=1,
设DE为x,EF=DE=x,EC=3-x,
x2=(3-x)2+1,
解得,x=
,
∴,
故选:B.
12.A
设旗杆的高度为m,则ACm,AB=m,BC=5m,
在中,
解得:
故选:A.
13.A
【分析】
设水池的深度BC=xm,则AB=(0.5+x)m,根据勾股定理列出方程,进而即可求解.
【详解】
解:在直角△ABC中,AC=1.5m.AB﹣BC=0.5m.
设水池的深度BC=xm,则AB=(0.5+x)m.
根据勾股定理得出:
∵AC2+BC2=AB2,
∴1.52+x2=(x+0.5)2,
解得:x=2.
故选:A.
14.B
如图所示:
∵AC=20m,BC=15m,
∴在Rt△ABC中,AB=m,
故选:B.
15.C
如图,
设学校教学楼的高度为,则,,,
左图,根据勾股定理得,绳长的平方,
右图,根据勾股定理得,绳长的平方,
∴,
解得:.
故选:C.
16.14.5
解:设秋千的绳索长为x尺,
由题意知:OC=x-(5-1)=(x-4)尺,CP′=10尺,OP′=x尺,
在Rt△OCP′中,由勾股定理得:
(x-4)?+10?=x?,
解得:x=14.5,
故答案为:14.5.
17.
如图所示,
∵楼梯的每一级的高宽长分别为20cm,宽40cm,长50cm,
∴(cm)
即蚂蚁从点A沿着台阶面爬行到点B的最短路程是130cm.
故答案为:130cm.
18.30
解:∵客船以24海里/时的速度从港口
A
向东北方向航行,
货船以18海里/时的速度同时从港口
A
向东南方向航行,
∴客船与货船方向的夹角为,
且客船行驶1小时的距离为24海里,货船行驶1小时的距离为18海里,
故两船1小时后的距离为海里,
故答案为:30.
19.12
解:依题意画出图形,设芦苇长AB=AB'=x尺,则水深AC=(x?1)尺,
因为B'E=10尺,所以B'C=5尺
在Rt△AB'C中,52+(x?1)2=x2,
解得:x=13,
即水深12尺,
故答案为:12
20.4.2尺.
解:如图所示:
由题意得:∠AOB=90°,
设折断处离地面的高度OA是x尺,
由勾股定理得:x2+42=(10﹣x)2,
解得:x=4.2,
即:折断后的竹子高度OA为4.2尺.
故答案为:4.2尺.
21.解:(1)由题意可得:
AC=24米,BC=7米,∠ACB=90°,
∴AB==25米,
∴梯子的长度为25米;
(2)如图,在Rt△CDE中,
∵CD=AC-4=24-4=20米,DE=25米,
∴CE==15米,
∴BE=CE-BC=15-7=8(米).
答:梯子底部在水平方向滑动了8米.
22.解:设BD为x米,且存在BD+DA=BC+CA,
即BD+DA=15,DA=15-x,
∵∠C=90°,
∴AD2=AC2+DC2,
∴(15-x)2=(x+5)2+102,
∴x=2.5,
∴CD=5+2.5=7.5,
答:树高7.5米.
23.(1)∵,即,
∴Rt△CHB是直角三角形,即CH⊥BH,
∴CH是从村庄C到河边的最近路(点到直线的距离中,垂线段最短);
(2)设AC=AB=x,则AH=x-1.8,
∵在Rt△ACH,
∴,即
,解得x=2.5,
∴原来的路线AC的长为2.5米.
24.
(海里),
(海里),
再Rt△ABC中,∠ABC=90°,
由勾股定理得:(海里),
∴返回所用时间为:小时,
出去所用时间为:小时,
∴则返回时比出去时节省的时间为:小时.
答:返回时比出去时节省了1小时.
25.解:在中,
米
,
,
所以小汽车超速了.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
