2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定自主学习优生提升训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定自主学习优生提升训练(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:25:00 | ||
图片预览



文档简介
2021年北师大版九年级数学上册《1.3正方形的性质与判定》自主学习
优生提升训练(附答案)
1.如图,在正方形ABCD中,点E、F分别在CD、BC上(不与端点重合),且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠AFB+∠BEC=90°
C.∠DAF=∠ABE D.AG⊥BE
2.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE?DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
3.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②AP=EF;③AP⊥EF;④EF的最小值为2;⑤△APD一定是等腰三角形.其中正确结论的序号为( )
A.2个 B.3个 C.4个 D.5个
4.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;
④∠AHB=∠EHD.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
5.如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
6.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为( )
A. B. C. D.2
7.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF的长为1,则△CEF的周长为( )
A.14 B.16 C.18 D.12
8.如图,在等腰Rt△ABC中,∠ACB=90°,AC=1,以斜边AB为边向外作正方形ABDE,连接CD,则CD的长为( )
A.2 B. C. D.
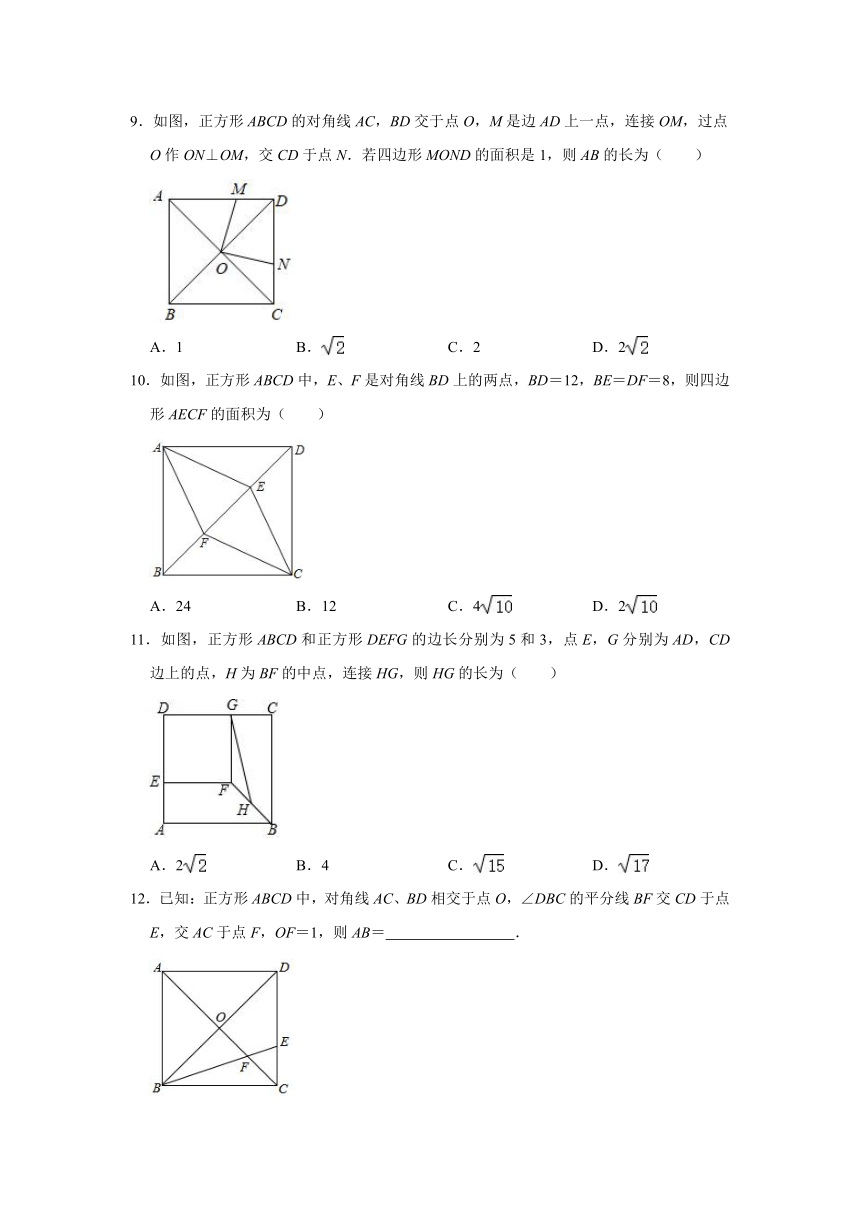
9.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
10.如图,正方形ABCD中,E、F是对角线BD上的两点,BD=12,BE=DF=8,则四边形AECF的面积为( )
A.24 B.12 C.4 D.2
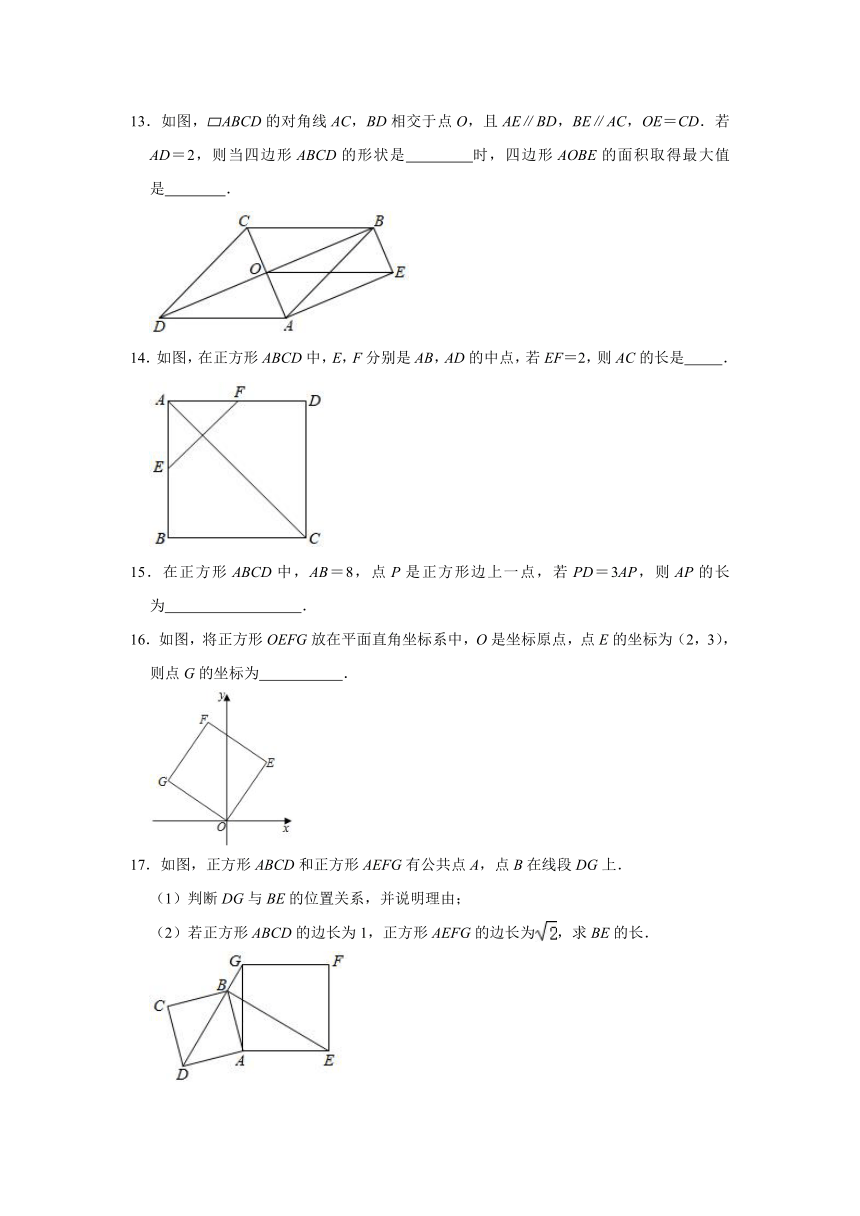
11.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E,G分别为AD,CD边上的点,H为BF的中点,连接HG,则HG的长为( )
A.2 B.4 C. D.
12.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB= .
13.如图,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.若AD=2,则当四边形ABCD的形状是 时,四边形AOBE的面积取得最大值是 .
14.如图,在正方形ABCD中,E,F分别是AB,AD的中点,若EF=2,则AC的长是 .
15.在正方形ABCD中,AB=8,点P是正方形边上一点,若PD=3AP,则AP的长为 .
16.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点G的坐标为 .
17.如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.
(1)判断DG与BE的位置关系,并说明理由;
(2)若正方形ABCD的边长为1,正方形AEFG的边长为,求BE的长.
18.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
19.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,求证:AB=FB.
20.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF.
(1)求证:△EBF≌△ABC;
(2)求证:四边形AEFD是平行四边形;
(3)△ABC满足 时,四边形AEFD是正方形.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠ABF=∠C=90°,AB=BC,
∵BF=CE,
∴△ABF≌△BCE(SAS),
∴AF=BE(A正确),∠BAF=∠CBE,∠AFB=∠BEC(B错误),
∵∠BAF+∠DAF=90°,∠ABE+∠EBC=90°,
∴∠DAF=∠ABE(C正确),
∵∠BAF=∠CBE,∠BAF+∠AFB=90°,
∴∠CBE+∠AFB=90°,
∴AG⊥BE(D正确),
所以不正确的是B,
故选:B.
2.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE?DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选:B.
3.解:∵PE⊥BC,PF⊥CD,
∴∠PEF=∠PFC=90°,
又∠C=90°,
∴四边形PECF是矩形,
∴EC=PF.
∵四边形ABCD是正方形,
∴∠PDF=45°,
∴△PDF是等腰直角三角形,
∴PD=PF=EC,①正确;
延长FP交AB于点N,延长AP交EF于点M.
∵四边形ABCD是正方形.
∴∠ABP=∠CBD
又∵NP⊥AB,PE⊥BC,
∴四边形BNPE是正方形,∠ANP=∠EPF,
∴NP=EP,
∴AN=PF
在△ANP与△FPE中,,
∴△ANP≌△FPE(SAS),
∴AP=EF;故②正确;
∠PFE=∠BAP,
△APN与△FPM中,∠APN=∠FPM,∠NAP=∠PFM,
∴∠PMF=∠ANP=90°,
∴AP⊥EF,故③正确;
∵矩形PECF中,EF=CP,
∴当CP⊥BD时,CP最小,即EF最小,
此时△BPC是等腰直角三角形,斜边为BC=4,
则CP=BC=2,
∴EF的最小值为2,故④正确;
∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故⑤错误.
故选:C.
4.解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°﹣90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,
即;S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.
5.解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°.
故选:A.
6.解:∵正方形ABCD的边长为,
∴OB=OC=BC=×=1,OB⊥OC,
∵CE=OC,
∴OE=2,
在Rt△OBE中,BE==.
故选:C.
7.解:在正方形ABCD中,BO=DO,BC=CD,∠BCD=90°,
∵F为DE的中点,
∴OF为△DBE的中位线,ED=2CF=2EF,
∴△CEF的周长为EF+EC+FC=ED+EC,
∵OF=1,
∴BE=2OF=2,
∵CE=6,
∴BC=BE+CE=2+6=8,
∴CD=BC=8,
在Rt△CED中,∠ECD=90°,CD=8,CE=6,
∴ED=,
∴△CEF的周长为EF+EC+FC=ED+EC=10+6=16,
故选:B.
8.解:过点D作DF⊥CB交CB的延长线于点F,如图,
∵Rt△ABC 是等腰直角三角形,
∴AC=CB=1,∠CAB+∠ABC﹣90°,
∵四边形ABDE 是正方形,
∴∠ABD=90°,AB=BD,
∴∠ABC+∠DBF=90°,
∴∠CAB=∠FBD,
在Rt△ACB和Rt△DFB中,
,
∴Rt△ACB≌Rt△DFB(AAS),
∴BF=AC,FD=CB,
∴BF=AC=FD=CB=1,
∴CF=CB+BF=1+1=2,
在Rt△CFD 中,由勾股定理得:CD=,
故选:C.
9.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∵AB2=4,
∴AB=2,
故选:C.
10.解:连接AC,
∵四边形ABCD是正方形,
∴AO=CO,BO=DO,AC⊥BD,AC=BD=12,
∴AO=CO=BO=DO,
∵BE=DF=8,
∴BF=DE=BD﹣BE=4,
∴OE=OF,EF=DF﹣DE=4,
∴四边形AECF是菱形,
∴菱形AECF的面积=AC?EF=×12×4=24,
故选:A.
11.解:延长GF交AB于P,过H作MN⊥CD于M,交AB于N,
∵四边形ABCD是正方形,
∴AB∥CD,BC⊥CD,
∴MN⊥AB,
∵四边形DEFG是正方形,
∴FG⊥CD,
∴FG∥HM∥BC,
∵H是BF的中点,
∴PN=BN=CM=GM=CG==1,
∴HN是△BFP的中位线,
∴HN=FP=1,
∴MH=5﹣1=4,
Rt△GHM中,由勾股定理得:GH===,
故选:D.
12.解:如图作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴BC=OB=2+.
故答案为2+.
13.解:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB.
∴平行四边形AEBO是矩形,
∴∠BOA=90°.
∴AC⊥BD.
∴平行四边形ABCD是菱形;
当AD=2时,四边形ABCD的形状是正方形,
AB=AD=2,OE=AB=2,
即四边形AOBE的面积取得最大值是2.
故答案为:正方形,2.
14.解:连接BD,如图所示:
∵E、F分别是AB,AD的中点,且EF=2,
∴EF是△ABD的中位线,
∴BD=2EF=2×2=4,
∵AC、BD是正方形ABCD的对角线,
∴AC=BD=4.
故答案为:4
15.解:当点P在AD上时,
∵PD=3AP,PD+AP=8,
∴AP=2,
当点P在AB上时,
∵PD2=AP2+AD2,
∴9AP2=AP2+64,
∴AP=2,
综上所述:AP=2或2,
故答案为2或2.
16.解:过E、G分别向x轴作垂线EA、EB,交x轴于A、B两点,
∵正方形OEFG,
∴OG=OE,∠GOE=90°,
∵∠GBO=∠EAO=90°,
∴∠GOB+∠AOE=90°,
∠GOB+∠BGO=90°,
∴∠AOE=∠BGO,
在△BOG与△AEO中
∴△BOG≌△AEO(AAS),
∴OB=AE=3,BG=OA=2,
∴G(﹣3,2),
故答案为:(﹣3,2).
17.解:(1)DG⊥BE,
理由如下:∵四边形ABCD,四边形AEFG是正方形,
∴AB=AD,∠DAB=∠GAE,AE=AG,∠ADB=∠ABD=45°,
∴∠DAG=∠BAE,
在△DAG和△BAE中,
,
∴△DAG≌△BAE(SAS).
∴DG=BE,∠ADG=∠ABE=45°,
∴∠ABD+∠ABE=90°,即∠GBE=90°.
∴DG⊥BE;
(2)连接GE,
∵正方形ABCD的边长为1,正方形AEFG的边长为,
∴BD=,GE=2,
设BE=x,则BG=x﹣,
在Rt△BGE中,利用勾股定理可得:
x2+(x﹣)2=22,
∴x=(+),
∴BE的长为().
18.(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8﹣6=2,CF=8+6=14,
在Rt△FCE中,EF===10.
19.证明:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,
∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
20.(1)证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,
即∠CBA=∠FBE,
在△EBF和△ABC中,
,
∴△EBF≌△ABC(SAS);
(2)证明:∵△EBF≌△ABC,
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴AB=AE=DF,
∴四边形AEFD是平行四边形;
(3)解:当AB=AC,∠BAC=150°时,四边形ADEF是正方形.
理由是:∵△ABE、△ACD为等边三角形,
∴AB=AE,AC=AD,∠EAB=∠DAC=60°,
∵AB=AC,
∴AE=AD,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∵∠BAC=150°,
∴∠EAD=360°﹣60°﹣60°﹣150°=90°,
∴平行四边形ADEF是正方形,
故答案为:AB=AC,∠BAC=150°
优生提升训练(附答案)
1.如图,在正方形ABCD中,点E、F分别在CD、BC上(不与端点重合),且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠AFB+∠BEC=90°
C.∠DAF=∠ABE D.AG⊥BE
2.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE?DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
3.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②AP=EF;③AP⊥EF;④EF的最小值为2;⑤△APD一定是等腰三角形.其中正确结论的序号为( )
A.2个 B.3个 C.4个 D.5个
4.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;
④∠AHB=∠EHD.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
5.如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
6.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为( )
A. B. C. D.2
7.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF的长为1,则△CEF的周长为( )
A.14 B.16 C.18 D.12
8.如图,在等腰Rt△ABC中,∠ACB=90°,AC=1,以斜边AB为边向外作正方形ABDE,连接CD,则CD的长为( )
A.2 B. C. D.
9.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
10.如图,正方形ABCD中,E、F是对角线BD上的两点,BD=12,BE=DF=8,则四边形AECF的面积为( )
A.24 B.12 C.4 D.2
11.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E,G分别为AD,CD边上的点,H为BF的中点,连接HG,则HG的长为( )
A.2 B.4 C. D.
12.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB= .
13.如图,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.若AD=2,则当四边形ABCD的形状是 时,四边形AOBE的面积取得最大值是 .
14.如图,在正方形ABCD中,E,F分别是AB,AD的中点,若EF=2,则AC的长是 .
15.在正方形ABCD中,AB=8,点P是正方形边上一点,若PD=3AP,则AP的长为 .
16.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点G的坐标为 .
17.如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.
(1)判断DG与BE的位置关系,并说明理由;
(2)若正方形ABCD的边长为1,正方形AEFG的边长为,求BE的长.
18.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
19.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,求证:AB=FB.
20.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF.
(1)求证:△EBF≌△ABC;
(2)求证:四边形AEFD是平行四边形;
(3)△ABC满足 时,四边形AEFD是正方形.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠ABF=∠C=90°,AB=BC,
∵BF=CE,
∴△ABF≌△BCE(SAS),
∴AF=BE(A正确),∠BAF=∠CBE,∠AFB=∠BEC(B错误),
∵∠BAF+∠DAF=90°,∠ABE+∠EBC=90°,
∴∠DAF=∠ABE(C正确),
∵∠BAF=∠CBE,∠BAF+∠AFB=90°,
∴∠CBE+∠AFB=90°,
∴AG⊥BE(D正确),
所以不正确的是B,
故选:B.
2.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
在Rt△OEN中,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
∴a+b=4,
∵CE?DE=5,
∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6,
∴S正方形ABCD=6,
故选:B.
3.解:∵PE⊥BC,PF⊥CD,
∴∠PEF=∠PFC=90°,
又∠C=90°,
∴四边形PECF是矩形,
∴EC=PF.
∵四边形ABCD是正方形,
∴∠PDF=45°,
∴△PDF是等腰直角三角形,
∴PD=PF=EC,①正确;
延长FP交AB于点N,延长AP交EF于点M.
∵四边形ABCD是正方形.
∴∠ABP=∠CBD
又∵NP⊥AB,PE⊥BC,
∴四边形BNPE是正方形,∠ANP=∠EPF,
∴NP=EP,
∴AN=PF
在△ANP与△FPE中,,
∴△ANP≌△FPE(SAS),
∴AP=EF;故②正确;
∠PFE=∠BAP,
△APN与△FPM中,∠APN=∠FPM,∠NAP=∠PFM,
∴∠PMF=∠ANP=90°,
∴AP⊥EF,故③正确;
∵矩形PECF中,EF=CP,
∴当CP⊥BD时,CP最小,即EF最小,
此时△BPC是等腰直角三角形,斜边为BC=4,
则CP=BC=2,
∴EF的最小值为2,故④正确;
∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故⑤错误.
故选:C.
4.解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°﹣90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,
即;S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.
5.解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°.
故选:A.
6.解:∵正方形ABCD的边长为,
∴OB=OC=BC=×=1,OB⊥OC,
∵CE=OC,
∴OE=2,
在Rt△OBE中,BE==.
故选:C.
7.解:在正方形ABCD中,BO=DO,BC=CD,∠BCD=90°,
∵F为DE的中点,
∴OF为△DBE的中位线,ED=2CF=2EF,
∴△CEF的周长为EF+EC+FC=ED+EC,
∵OF=1,
∴BE=2OF=2,
∵CE=6,
∴BC=BE+CE=2+6=8,
∴CD=BC=8,
在Rt△CED中,∠ECD=90°,CD=8,CE=6,
∴ED=,
∴△CEF的周长为EF+EC+FC=ED+EC=10+6=16,
故选:B.
8.解:过点D作DF⊥CB交CB的延长线于点F,如图,
∵Rt△ABC 是等腰直角三角形,
∴AC=CB=1,∠CAB+∠ABC﹣90°,
∵四边形ABDE 是正方形,
∴∠ABD=90°,AB=BD,
∴∠ABC+∠DBF=90°,
∴∠CAB=∠FBD,
在Rt△ACB和Rt△DFB中,
,
∴Rt△ACB≌Rt△DFB(AAS),
∴BF=AC,FD=CB,
∴BF=AC=FD=CB=1,
∴CF=CB+BF=1+1=2,
在Rt△CFD 中,由勾股定理得:CD=,
故选:C.
9.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∵AB2=4,
∴AB=2,
故选:C.
10.解:连接AC,
∵四边形ABCD是正方形,
∴AO=CO,BO=DO,AC⊥BD,AC=BD=12,
∴AO=CO=BO=DO,
∵BE=DF=8,
∴BF=DE=BD﹣BE=4,
∴OE=OF,EF=DF﹣DE=4,
∴四边形AECF是菱形,
∴菱形AECF的面积=AC?EF=×12×4=24,
故选:A.
11.解:延长GF交AB于P,过H作MN⊥CD于M,交AB于N,
∵四边形ABCD是正方形,
∴AB∥CD,BC⊥CD,
∴MN⊥AB,
∵四边形DEFG是正方形,
∴FG⊥CD,
∴FG∥HM∥BC,
∵H是BF的中点,
∴PN=BN=CM=GM=CG==1,
∴HN是△BFP的中位线,
∴HN=FP=1,
∴MH=5﹣1=4,
Rt△GHM中,由勾股定理得:GH===,
故选:D.
12.解:如图作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴BC=OB=2+.
故答案为2+.
13.解:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB.
∴平行四边形AEBO是矩形,
∴∠BOA=90°.
∴AC⊥BD.
∴平行四边形ABCD是菱形;
当AD=2时,四边形ABCD的形状是正方形,
AB=AD=2,OE=AB=2,
即四边形AOBE的面积取得最大值是2.
故答案为:正方形,2.
14.解:连接BD,如图所示:
∵E、F分别是AB,AD的中点,且EF=2,
∴EF是△ABD的中位线,
∴BD=2EF=2×2=4,
∵AC、BD是正方形ABCD的对角线,
∴AC=BD=4.
故答案为:4
15.解:当点P在AD上时,
∵PD=3AP,PD+AP=8,
∴AP=2,
当点P在AB上时,
∵PD2=AP2+AD2,
∴9AP2=AP2+64,
∴AP=2,
综上所述:AP=2或2,
故答案为2或2.
16.解:过E、G分别向x轴作垂线EA、EB,交x轴于A、B两点,
∵正方形OEFG,
∴OG=OE,∠GOE=90°,
∵∠GBO=∠EAO=90°,
∴∠GOB+∠AOE=90°,
∠GOB+∠BGO=90°,
∴∠AOE=∠BGO,
在△BOG与△AEO中
∴△BOG≌△AEO(AAS),
∴OB=AE=3,BG=OA=2,
∴G(﹣3,2),
故答案为:(﹣3,2).
17.解:(1)DG⊥BE,
理由如下:∵四边形ABCD,四边形AEFG是正方形,
∴AB=AD,∠DAB=∠GAE,AE=AG,∠ADB=∠ABD=45°,
∴∠DAG=∠BAE,
在△DAG和△BAE中,
,
∴△DAG≌△BAE(SAS).
∴DG=BE,∠ADG=∠ABE=45°,
∴∠ABD+∠ABE=90°,即∠GBE=90°.
∴DG⊥BE;
(2)连接GE,
∵正方形ABCD的边长为1,正方形AEFG的边长为,
∴BD=,GE=2,
设BE=x,则BG=x﹣,
在Rt△BGE中,利用勾股定理可得:
x2+(x﹣)2=22,
∴x=(+),
∴BE的长为().
18.(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8﹣6=2,CF=8+6=14,
在Rt△FCE中,EF===10.
19.证明:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,
∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
20.(1)证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,
即∠CBA=∠FBE,
在△EBF和△ABC中,
,
∴△EBF≌△ABC(SAS);
(2)证明:∵△EBF≌△ABC,
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴AB=AE=DF,
∴四边形AEFD是平行四边形;
(3)解:当AB=AC,∠BAC=150°时,四边形ADEF是正方形.
理由是:∵△ABE、△ACD为等边三角形,
∴AB=AE,AC=AD,∠EAB=∠DAC=60°,
∵AB=AC,
∴AE=AD,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∵∠BAC=150°,
∴∠EAD=360°﹣60°﹣60°﹣150°=90°,
∴平行四边形ADEF是正方形,
故答案为:AB=AC,∠BAC=150°
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
