人教版八上高分笔记之导与练 11.2.1.1 三角形的内角和(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 11.2.1.1 三角形的内角和(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.2与三角形有关的角
三角形的内角和
知识点:三角形内角和定理:
.
易错点睛
在ΔABC中,∠A=∠B=∠C.则∠C的度数为________
【点晴】设∠A=x,根据三角形内角和定理列方程求解即可,
典型例题
题型一
三角形内角和定理的有关计算
如图,在ΔABC?中,BD是∠ABC的平分线,ED//BC,且∠A=60°,∠C=76°,则∠BDE的度数为(
)
A.20°
B.22°
C.44°
D.82°
变式练习:
1.[教材P16习题11.2T5变式题]如图,AC与BD相交于点0,AB//CD,∠AOB=105°,∠B=30°,则∠C的度数为(????)
A.45°
B.55°
C.60°
D.75°
第1题
第2题
2.一副直角三角尺按如图所示的方式摆放,点D在BC的延长线上,EF//BC,∠B=∠EDF=90°,∠A=30°,∠F=45°,则∠CED=___________
题型二、利用三角形的内角和解决折叠中角度计算
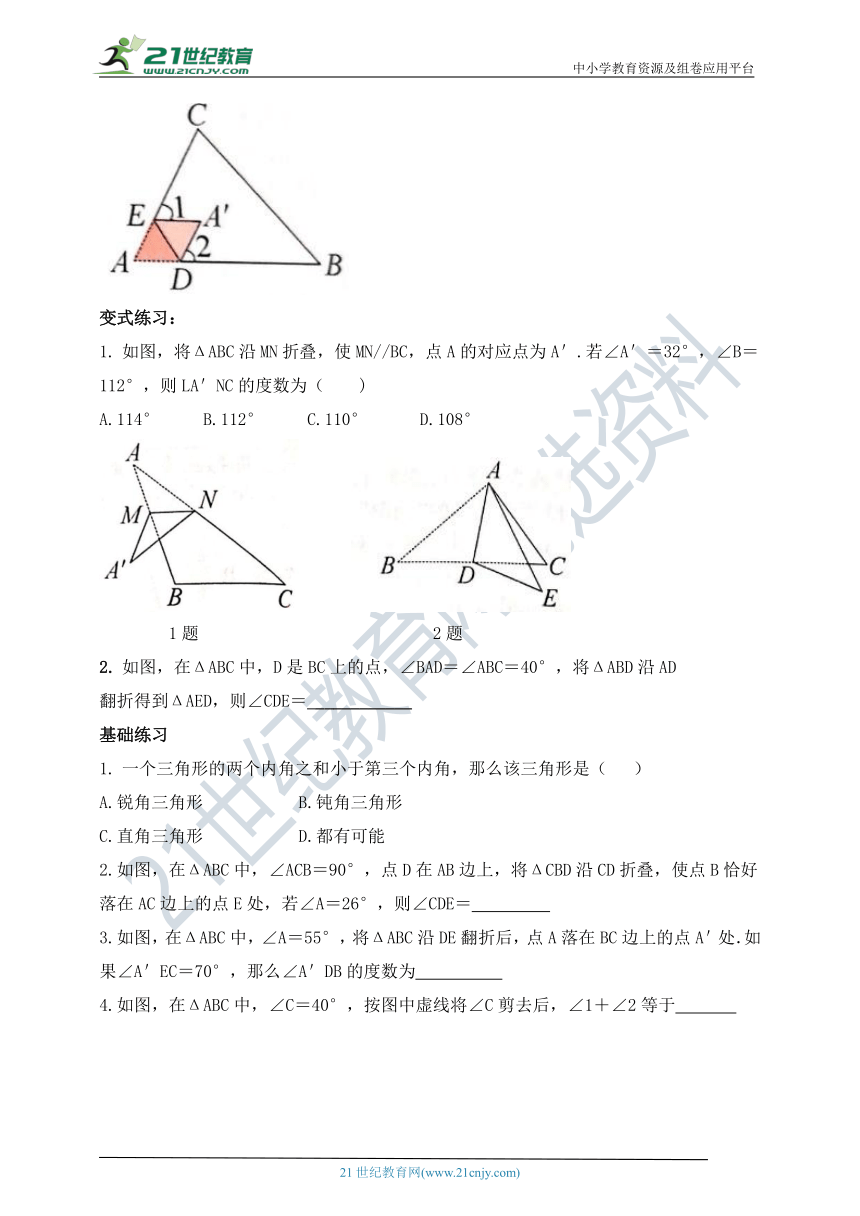
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2等于(
)
A.
140°???
B.
220°???
C.
110°???
D.
70°
变式练习:
如图,将ΔABC沿MN折叠,使MN//BC,点A的对应点为A'.若∠A'=32°,∠B=112°,则LA'NC的度数为(
?)
A.114°
B.112°
C.110°
D.108°
1题
2题
如图,在ΔABC中,D是BC上的点,∠BAD=∠ABC=40°,将ΔABD沿AD
翻折得到ΔAED,则∠CDE=
___________
基础练习
一个三角形的两个内角之和小于第三个内角,那么该三角形是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.都有可能
2.如图,在ΔABC中,∠ACB=90°,点D在AB边上,将ΔCBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE=
3.如图,在ΔABC中,∠A=55°,将ΔABC沿DE翻折后,点A落在BC边上的点A'处.如果∠A'EC=70°,那么∠A'DB的度数为
4.如图,在ΔABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于
第2题
第3题
第4题
第5题
5.如图,点D在ΔABC内,∠BDC=120°,∠1+∠2=55°,则∠A的度数为
6.如图,在ΔABC中,∠B=40°,∠C=60°,点D,E分别在边BC,AC上,且DE//AB,若∠CAD=25°,求∠ADE的度数.
7.如图,在ΔABC中,∠1=∠2,∠BAC=65°,求∠APB的度数.
综合题探究
8.(1)【问题背景】如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D之间的数量关系是_________?
(2)【尝试运用】如图2,AP,CP分别平分∠BAD,∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)【拓展创新】如图3,CP,AG分别平分∠BCE,∠FAD,AG的反向延长线交CP于点P,∠B+∠D=60°,求∠P的度数.
答案:
知识点:三角形内角和定理:三角形三个内角的和等于180°.
易错点睛
在ΔABC中,∠A=∠B=∠C.则∠C的度数为900
【点晴】设∠A=x,根据三角形内角和定理列方程求解即可,
典型例题
题型一
三角形内角和定理的有关计算
如图,在ΔABC?中,BD是∠ABC的平分线,ED//BC,且∠A=60°,∠C=76°,则∠BDE的度数为(
)
A.20°
B.22°
C.44°
D.82°
在△ABC中,∵∠A=60°,∠C=76°,
∴∠ABC=180°-∠A-∠C=44°,
∵BD是∠ABC的角平分线,
∴∠CBD=∠ABC=22°,
∵DE∥BC,
∴∠EDB=∠DBC=22°,
故选B
点评
利用平行线的性质将所求的角转化到已知角所在三角形中是解决此类问题的关键。
变式练习:
1.[教材P16习题11.2T5变式题]如图,AC与BD相交于点0,AB//CD,∠AOB=105°,∠B=30°,则∠C的度数为(??A??)
A.45°
B.55°
C.60°
D.75°
第1题
第2题
2.一副直角三角尺按如图所示的方式摆放,点D在BC的延长线上,EF//BC,∠B=∠EDF=90°,∠A=30°,∠F=45°,则∠CED=150
题型二、利用三角形的内角和解决折叠中角度计算
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2等于(
)
A.
140°???
B.
220°???
C.
110°???
D.
70°
由题意分析,将△ABC沿着DE折叠压平,A与A′重合,则有:
,由题知,
故选A
点评:通过图形的分析,图形的折叠,得到各个角的基本关系,进而得出所求的基本关系
变式练习:
如图,将ΔABC沿MN折叠,使MN//BC,点A的对应点为A'.若∠A'=32°,∠B=112°,则LA'NC的度数为(
D??)
A.114°
B.112°
C.110°
D.108°
1题
2题
如图,在ΔABC中,D是BC上的点,∠BAD=∠ABC=40°,将ΔABD沿AD
翻折得到ΔAED,则∠CDE=20°
基础练习
一个三角形的两个内角之和小于第三个内角,那么该三角形是(
B
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.都有可能
2.如图,在ΔABC中,∠ACB=90°,点D在AB边上,将ΔCBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE=71°
3.如图,在ΔABC中,∠A=55°,将ΔABC沿DE翻折后,点A落在BC边上的点A'处.如果∠A'EC=70°,那么∠A'DB的度数为40°
4.如图,在ΔABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于220°
第2题
第3题
第4题
第5题
5.如图,点D在ΔABC内,∠BDC=120°,∠1+∠2=55°,则∠A的度数为650
6.如图,在ΔABC中,∠B=40°,∠C=60°,点D,E分别在边BC,AC上,且DE//AB,若∠CAD=25°,求∠ADE的度数.
解:在ΔABC中,∠BAC+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°,?
∴∠BAD=∠BAC-∠CAD.∠CAD=25°,∴∠BAD=80°-25°=55°,?
∵DE//AB,∴∠ADE=∠BAD,∴∠ADE=55°.?
7.如图,在ΔABC中,∠1=∠2,∠BAC=65°,求∠APB的度数.
解:∵∠1=∠2,∠BAC=∠BAP+∠2=65°,∴∠BAP+∠1=65°,
∵∠1+∠BAP+∠P=180°,∴65°+∠P=180°,∴∠APB=115°.?
综合题探究
8.(1)【问题背景】如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D之间的数量关系是_________?
(2)【尝试运用】如图2,AP,CP分别平分∠BAD,∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)【拓展创新】如图3,CP,AG分别平分∠BCE,∠FAD,AG的反向延长线交CP于点P,∠B+∠D=60°,求∠P的度数.
解:(1)∠A+∠B=∠C+∠D;
(2)∵AP平分∠BAD,∴∠1=∠2,
∵PC平分∠BCD,∴∠3=∠4,
∵∠1+∠B=∠3+∠P①,
∠2+∠P=∠4+∠D②,
②得,2∠P=∠B+∠D=50°,∴∠P=25°;
(3)∵CP平分∠BCE,∴∠3=∠4,
∵AG平分∠DAF,∴∠1=∠2.
∵∠PAB=∠1,
∴∠2=∠PAB,∵∠P+∠PAB=∠B+∠4,∴∠P+∠2=∠B+∠4①,?
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°-∠2)=∠D+(180°-∠3)②,?
①+②得,2∠P=∠B+∠D=60°∴∠P=30°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.2与三角形有关的角
三角形的内角和
知识点:三角形内角和定理:
.
易错点睛
在ΔABC中,∠A=∠B=∠C.则∠C的度数为________
【点晴】设∠A=x,根据三角形内角和定理列方程求解即可,
典型例题
题型一
三角形内角和定理的有关计算
如图,在ΔABC?中,BD是∠ABC的平分线,ED//BC,且∠A=60°,∠C=76°,则∠BDE的度数为(
)
A.20°
B.22°
C.44°
D.82°
变式练习:
1.[教材P16习题11.2T5变式题]如图,AC与BD相交于点0,AB//CD,∠AOB=105°,∠B=30°,则∠C的度数为(????)
A.45°
B.55°
C.60°
D.75°
第1题
第2题
2.一副直角三角尺按如图所示的方式摆放,点D在BC的延长线上,EF//BC,∠B=∠EDF=90°,∠A=30°,∠F=45°,则∠CED=___________
题型二、利用三角形的内角和解决折叠中角度计算
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2等于(
)
A.
140°???
B.
220°???
C.
110°???
D.
70°
变式练习:
如图,将ΔABC沿MN折叠,使MN//BC,点A的对应点为A'.若∠A'=32°,∠B=112°,则LA'NC的度数为(
?)
A.114°
B.112°
C.110°
D.108°
1题
2题
如图,在ΔABC中,D是BC上的点,∠BAD=∠ABC=40°,将ΔABD沿AD
翻折得到ΔAED,则∠CDE=
___________
基础练习
一个三角形的两个内角之和小于第三个内角,那么该三角形是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.都有可能
2.如图,在ΔABC中,∠ACB=90°,点D在AB边上,将ΔCBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE=
3.如图,在ΔABC中,∠A=55°,将ΔABC沿DE翻折后,点A落在BC边上的点A'处.如果∠A'EC=70°,那么∠A'DB的度数为
4.如图,在ΔABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于
第2题
第3题
第4题
第5题
5.如图,点D在ΔABC内,∠BDC=120°,∠1+∠2=55°,则∠A的度数为
6.如图,在ΔABC中,∠B=40°,∠C=60°,点D,E分别在边BC,AC上,且DE//AB,若∠CAD=25°,求∠ADE的度数.
7.如图,在ΔABC中,∠1=∠2,∠BAC=65°,求∠APB的度数.
综合题探究
8.(1)【问题背景】如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D之间的数量关系是_________?
(2)【尝试运用】如图2,AP,CP分别平分∠BAD,∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)【拓展创新】如图3,CP,AG分别平分∠BCE,∠FAD,AG的反向延长线交CP于点P,∠B+∠D=60°,求∠P的度数.
答案:
知识点:三角形内角和定理:三角形三个内角的和等于180°.
易错点睛
在ΔABC中,∠A=∠B=∠C.则∠C的度数为900
【点晴】设∠A=x,根据三角形内角和定理列方程求解即可,
典型例题
题型一
三角形内角和定理的有关计算
如图,在ΔABC?中,BD是∠ABC的平分线,ED//BC,且∠A=60°,∠C=76°,则∠BDE的度数为(
)
A.20°
B.22°
C.44°
D.82°
在△ABC中,∵∠A=60°,∠C=76°,
∴∠ABC=180°-∠A-∠C=44°,
∵BD是∠ABC的角平分线,
∴∠CBD=∠ABC=22°,
∵DE∥BC,
∴∠EDB=∠DBC=22°,
故选B
点评
利用平行线的性质将所求的角转化到已知角所在三角形中是解决此类问题的关键。
变式练习:
1.[教材P16习题11.2T5变式题]如图,AC与BD相交于点0,AB//CD,∠AOB=105°,∠B=30°,则∠C的度数为(??A??)
A.45°
B.55°
C.60°
D.75°
第1题
第2题
2.一副直角三角尺按如图所示的方式摆放,点D在BC的延长线上,EF//BC,∠B=∠EDF=90°,∠A=30°,∠F=45°,则∠CED=150
题型二、利用三角形的内角和解决折叠中角度计算
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2等于(
)
A.
140°???
B.
220°???
C.
110°???
D.
70°
由题意分析,将△ABC沿着DE折叠压平,A与A′重合,则有:
,由题知,
故选A
点评:通过图形的分析,图形的折叠,得到各个角的基本关系,进而得出所求的基本关系
变式练习:
如图,将ΔABC沿MN折叠,使MN//BC,点A的对应点为A'.若∠A'=32°,∠B=112°,则LA'NC的度数为(
D??)
A.114°
B.112°
C.110°
D.108°
1题
2题
如图,在ΔABC中,D是BC上的点,∠BAD=∠ABC=40°,将ΔABD沿AD
翻折得到ΔAED,则∠CDE=20°
基础练习
一个三角形的两个内角之和小于第三个内角,那么该三角形是(
B
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.都有可能
2.如图,在ΔABC中,∠ACB=90°,点D在AB边上,将ΔCBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE=71°
3.如图,在ΔABC中,∠A=55°,将ΔABC沿DE翻折后,点A落在BC边上的点A'处.如果∠A'EC=70°,那么∠A'DB的度数为40°
4.如图,在ΔABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于220°
第2题
第3题
第4题
第5题
5.如图,点D在ΔABC内,∠BDC=120°,∠1+∠2=55°,则∠A的度数为650
6.如图,在ΔABC中,∠B=40°,∠C=60°,点D,E分别在边BC,AC上,且DE//AB,若∠CAD=25°,求∠ADE的度数.
解:在ΔABC中,∠BAC+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°,?
∴∠BAD=∠BAC-∠CAD.∠CAD=25°,∴∠BAD=80°-25°=55°,?
∵DE//AB,∴∠ADE=∠BAD,∴∠ADE=55°.?
7.如图,在ΔABC中,∠1=∠2,∠BAC=65°,求∠APB的度数.
解:∵∠1=∠2,∠BAC=∠BAP+∠2=65°,∴∠BAP+∠1=65°,
∵∠1+∠BAP+∠P=180°,∴65°+∠P=180°,∴∠APB=115°.?
综合题探究
8.(1)【问题背景】如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D之间的数量关系是_________?
(2)【尝试运用】如图2,AP,CP分别平分∠BAD,∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)【拓展创新】如图3,CP,AG分别平分∠BCE,∠FAD,AG的反向延长线交CP于点P,∠B+∠D=60°,求∠P的度数.
解:(1)∠A+∠B=∠C+∠D;
(2)∵AP平分∠BAD,∴∠1=∠2,
∵PC平分∠BCD,∴∠3=∠4,
∵∠1+∠B=∠3+∠P①,
∠2+∠P=∠4+∠D②,
②得,2∠P=∠B+∠D=50°,∴∠P=25°;
(3)∵CP平分∠BCE,∴∠3=∠4,
∵AG平分∠DAF,∴∠1=∠2.
∵∠PAB=∠1,
∴∠2=∠PAB,∵∠P+∠PAB=∠B+∠4,∴∠P+∠2=∠B+∠4①,?
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°-∠2)=∠D+(180°-∠3)②,?
①+②得,2∠P=∠B+∠D=60°∴∠P=30°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
