山东省烟台市2012届高三适应性练习一(二模)数学(理)试题
文档属性
| 名称 | 山东省烟台市2012届高三适应性练习一(二模)数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 21:51:19 | ||
图片预览




文档简介
2012年高三适应性练习(一)
数学(理科)
参考公式:
锥体的体积公式,其中S是锥体的底面积,h是锥体的高.
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概率为
注意事项:
1.本试题满分150分,考试时间为120分钟.
2.使用答题纸时,必须使用0.5毫米的黑色墨水签字笔书写,作图时,可用2B铅笔.要字迹工整,笔迹清晰.超出答题区书写的答案无效;在草稿纸,试题卷上答题无效.
3.答卷前将密封线内的项目填写清楚.
一、选择题:本大题共12小题;每小题5分,共60分.每小题给出的四个选项中,只有一个选项是符合题目要求的,把正确选项的代号涂在答题卡上.
1.设全集,,则
A. B. C. D.
2.已知复数,若在复平面上对应的点在虚轴上,则a的值是
A. B. C.2 D.
3.下列命题正确的是
A. B.>x2
C.x>1是x2>1的充分不必要条件 D.若a>b,则a2>b2
4.点P在边长为1的正方形ABCD内运动,则动点P到顶点A的距离<1的概率为
A. B. C. D.
5.已知倾斜角为的直线与直线平行,则tan的值为
A. B. C. D.
6.已知数据x1,x2,x3,…,xn是某企业普通职工个人的年收入,设这个n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可以不变,中位数可能不变,方差可能不变。
7.已知向量且,若变量x,y满足约束条件,则z的最大值为
A.1 B.2 C.3 D.4
8.设随机变量服从正态分布N(2,9),若>c+=<,则c=
A.1 B.2 C.3 D.4
9.某几何体的三视图如右图所示,已知其正视图的周长为6,则该 几何体体积的最大值为
A. B. C. D.2
10.已知F1,F2是椭圆(a>b>0)的左、右焦点,点P在椭圆上,且记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1:2,则该椭圆的离心率等于
A. B. C. D.
11.函数y=x+sin,的大致图象是
12.若偶函数满足,且当时,,则函数的零点个数为
A.7 B.8 C.9 D.10
二、填空题.本大题共有4个小题,每小题4分,共16分.把正确答案填在答题卡的相应位置.
13.执行右图所示的程序框图,若输入x=2,则输出y的值为
14.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门相同的选法种数为(用数字作答)
15.已知函数若,且,都有不等式成立,则若实数x的取值范围是
16.已知函数是R上的偶函数,对都有成立.当,且时,都有<0,给出下列命题:
(1);(2)直线是函数图象的一条对称轴;
(3)函数在上有四个零点;(4)
其中所有正确命题的序号为
二、解答题.本大题共6个小题,共74分.解答应写出文字说明、证明过程或推演步骤.
17.(本小题满分12分)
在锐角三角形ABC中,a、b、c分别是角A、B、C的对边,且m//n.
(1)求角A的大小;
(2)求函数的值域.
18.(本小题满分12分)
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款共利润为1.5万元;分4期或5期付款,其利润为2万元.用表示经销一辆汽车的利润.
付款方式 分1期 分2期 分3期 分4期 分5期
频数 40 20 a 10 b
(1)求上表中的a,b值;
(2)若以频率作为概率,求事件A: “购买该器重汽车的3位顾客中,至多有1位采用3期付款”的概率P(A);
(3)求的分布列及数学期望E.
19.(本小题满分12分)
已知
(1)求证:数列是等比数列;
(2)求证:
20.(本小题满分12分)
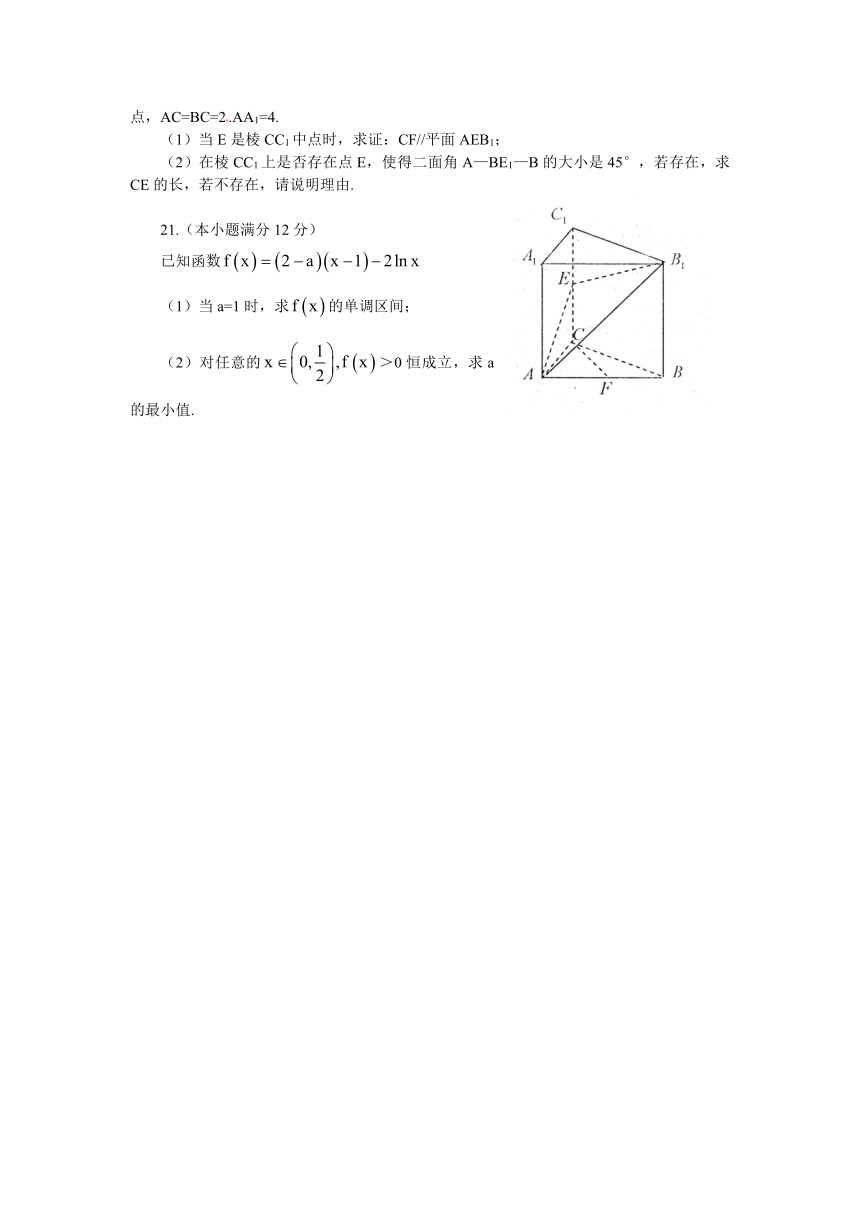
如图,已知直三棱柱ABC—A1B1C1,°,E是棱CC1上动点,F是AB中点,AC=BC=2.AA1=4.
(1)当E是棱CC1中点时,求证:CF//平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A—BE1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由.
21.(本小题满分12分)
已知函数
(1)当a=1时,求的单调区间;
(2)对任意的>0恒成立,求a的最小值.
22.(本小题满分14分)
如图,过抛物线焦点F的直线与抛物线交点点A,B(A在第一象限),点C(t>1).
(1)若△CBF,△CFA,△CBA的面积成等差数列,求直线l的方程;
(2)若,且FAC为锐角,试求t的取值范围.
2012年高三适应性练习(一)
数学试题(理)参考答案
数学(理科)
参考公式:
锥体的体积公式,其中S是锥体的底面积,h是锥体的高.
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概率为
注意事项:
1.本试题满分150分,考试时间为120分钟.
2.使用答题纸时,必须使用0.5毫米的黑色墨水签字笔书写,作图时,可用2B铅笔.要字迹工整,笔迹清晰.超出答题区书写的答案无效;在草稿纸,试题卷上答题无效.
3.答卷前将密封线内的项目填写清楚.
一、选择题:本大题共12小题;每小题5分,共60分.每小题给出的四个选项中,只有一个选项是符合题目要求的,把正确选项的代号涂在答题卡上.
1.设全集,,则
A. B. C. D.
2.已知复数,若在复平面上对应的点在虚轴上,则a的值是
A. B. C.2 D.
3.下列命题正确的是
A. B.>x2
C.x>1是x2>1的充分不必要条件 D.若a>b,则a2>b2
4.点P在边长为1的正方形ABCD内运动,则动点P到顶点A的距离<1的概率为
A. B. C. D.
5.已知倾斜角为的直线与直线平行,则tan的值为
A. B. C. D.
6.已知数据x1,x2,x3,…,xn是某企业普通职工个人的年收入,设这个n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可以不变,中位数可能不变,方差可能不变。
7.已知向量且,若变量x,y满足约束条件,则z的最大值为
A.1 B.2 C.3 D.4
8.设随机变量服从正态分布N(2,9),若>c+=<,则c=
A.1 B.2 C.3 D.4
9.某几何体的三视图如右图所示,已知其正视图的周长为6,则该 几何体体积的最大值为
A. B. C. D.2
10.已知F1,F2是椭圆(a>b>0)的左、右焦点,点P在椭圆上,且记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1:2,则该椭圆的离心率等于
A. B. C. D.
11.函数y=x+sin,的大致图象是
12.若偶函数满足,且当时,,则函数的零点个数为
A.7 B.8 C.9 D.10
二、填空题.本大题共有4个小题,每小题4分,共16分.把正确答案填在答题卡的相应位置.
13.执行右图所示的程序框图,若输入x=2,则输出y的值为
14.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门相同的选法种数为(用数字作答)
15.已知函数若,且,都有不等式成立,则若实数x的取值范围是
16.已知函数是R上的偶函数,对都有成立.当,且时,都有<0,给出下列命题:
(1);(2)直线是函数图象的一条对称轴;
(3)函数在上有四个零点;(4)
其中所有正确命题的序号为
二、解答题.本大题共6个小题,共74分.解答应写出文字说明、证明过程或推演步骤.
17.(本小题满分12分)
在锐角三角形ABC中,a、b、c分别是角A、B、C的对边,且m//n.
(1)求角A的大小;
(2)求函数的值域.
18.(本小题满分12分)
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款共利润为1.5万元;分4期或5期付款,其利润为2万元.用表示经销一辆汽车的利润.
付款方式 分1期 分2期 分3期 分4期 分5期
频数 40 20 a 10 b
(1)求上表中的a,b值;
(2)若以频率作为概率,求事件A: “购买该器重汽车的3位顾客中,至多有1位采用3期付款”的概率P(A);
(3)求的分布列及数学期望E.
19.(本小题满分12分)
已知
(1)求证:数列是等比数列;
(2)求证:
20.(本小题满分12分)
如图,已知直三棱柱ABC—A1B1C1,°,E是棱CC1上动点,F是AB中点,AC=BC=2.AA1=4.
(1)当E是棱CC1中点时,求证:CF//平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A—BE1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由.
21.(本小题满分12分)
已知函数
(1)当a=1时,求的单调区间;
(2)对任意的>0恒成立,求a的最小值.
22.(本小题满分14分)
如图,过抛物线焦点F的直线与抛物线交点点A,B(A在第一象限),点C(t>1).
(1)若△CBF,△CFA,△CBA的面积成等差数列,求直线l的方程;
(2)若,且FAC为锐角,试求t的取值范围.
2012年高三适应性练习(一)
数学试题(理)参考答案
同课章节目录
