4.4.2相似三角形的判别方法二 同步课件 2021-2022学年九年级数学北师大版上册(共18张ppt)
文档属性
| 名称 | 4.4.2相似三角形的判别方法二 同步课件 2021-2022学年九年级数学北师大版上册(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 564.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 15:04:55 | ||
图片预览



文档简介
4.4.2 相似三角形的判定2
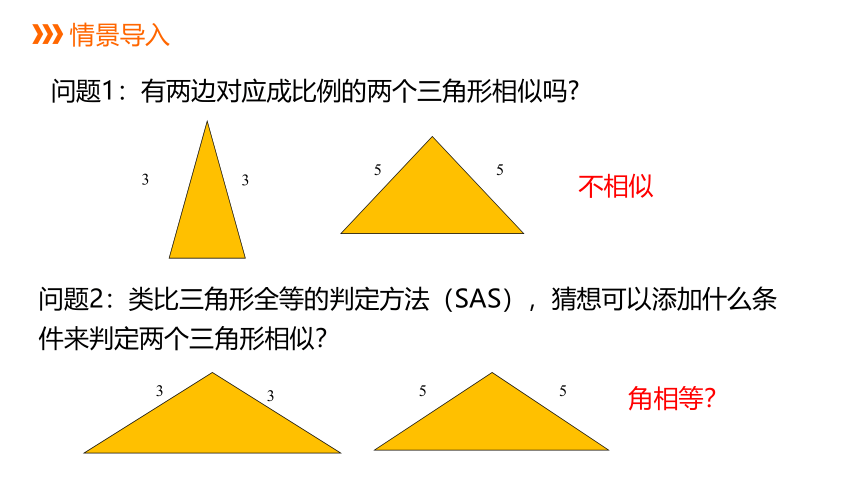
问题1:有两边对应成比例的两个三角形相似吗?
3
3
5
5
不相似
问题2:类比三角形全等的判定方法(SAS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
角相等?
情景导入
学习目标
1.掌握相似三角形的判定定理2;(重点)
2.能熟练运用相似三角形的判定定理2.(难点)
2.改变k值的大小,再试一试。
1.画△ABC与△A'B'C',使∠A=∠A', 设法比较∠B与∠B'的大小(或∠C与∠C').△ABC和△A'B'C'相似吗?
两个三角形相似
获取新知
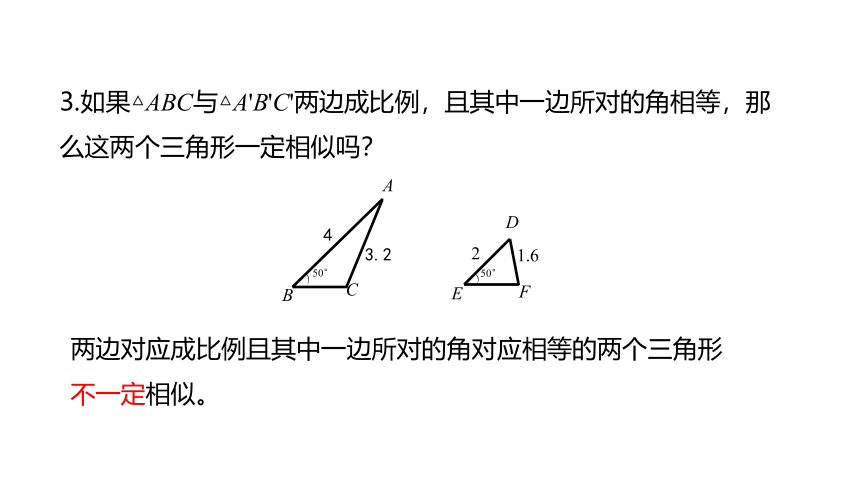
3.如果△ABC与△A'B'C'两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?
50°
)
4
A
B
C
3.2
2
50°
)
E
D
F
1.6
两边对应成比例且其中一边所对的角对应相等的两个三角形
不一定相似。
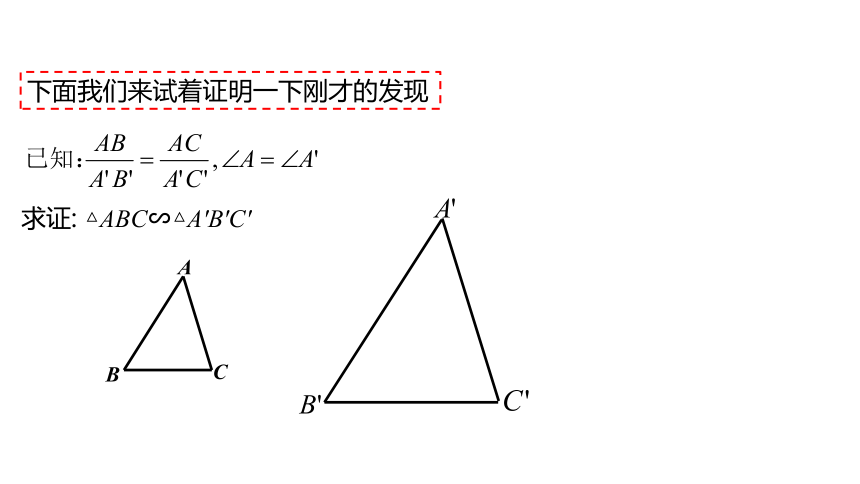
求证: △ABC∽△A'B'C'
A
B
C
下面我们来试着证明一下刚才的发现
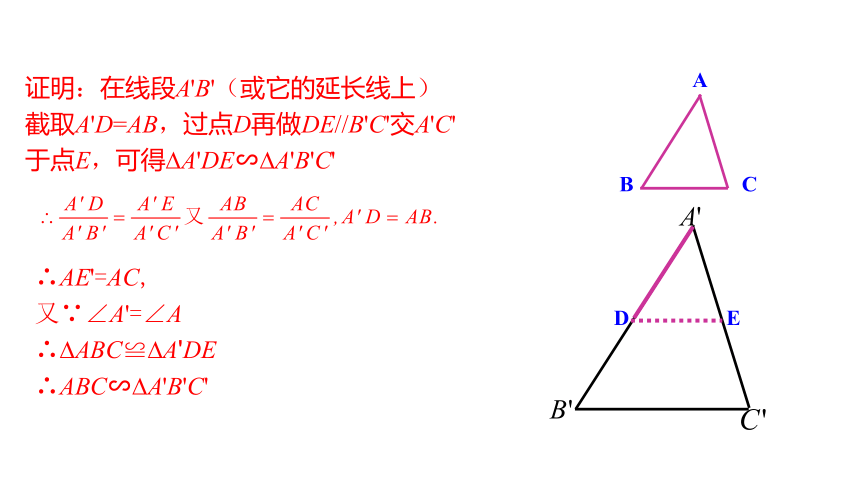
A
B
C
D
E
证明:在线段A'B'(或它的延长线上)截取A'D=AB,过点D再做DE//B'C'交A'C'于点E,可得?A'DE∽?A'B'C'
∴AE'=AC,
又∵∠A'=∠A
∴?ABC≌?A'DE
∴ABC∽?A'B'C'
相似三角形判定定理2:
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
∴ABC∽?A'B'C'
符号语言:
B
A
C
B'
A'
C'
例1 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
解:∵ AE=1.5,AC=2,
∴
又∵∠EAD=∠CAB,
∴ △ADE ∽△ABC,
∴
∴
提示:
解题时要找准对应边.
例题讲解
(2)∵△ACD∽△CBD
∴∠A=∠BCD.
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°.
即∠ACB=90°.
解:(1)证明:∵CD是边AB上的高
∴∠ADC=∠CDB=90°
又CD2=AD·BD
∴
∴△ACD∽△CBD
【归纳总结】利用两边及夹角判定三角形相似的策略:
(1)角与边的联系:角是对应边的夹角,边是此对应角的两边.
一定要注意:与对应角的对边无关.
(2)找条件:已知条件中有明确的比例关系式时,只要证明与比例关系式相关的两边的夹角相等即可.
注意利用图形中的隐含条件,如:公共角、对顶角等.
C
1.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
随堂演练
2.在△ABC和△A1B1C1中,下列四个命题:
(1)若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC∶A1C1=CB∶C1B1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4 B.3 C.2 D.1
B
3、如图,给出下列条件:?
① ∠B=∠ACD;?
② ∠ADC=∠ACB;
③ ;
④ AC?=AD·AB,
其中能够判△ABC∽△ACD的有( )
A.1个 B.2个 C.3个 D.4个
C
4.如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和△ABC相似,则AQ的长为 .
5. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,
求证 △ABC ∽△AED.
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
A
B
C
D
E
思维拓展
如图,在边长为2个单位长度的正方形ABCD中,E是AB的中点,点P从点D出发沿射线DC以每秒1个单位长度的速度运动,过点P作PF⊥DE于点F,当运动时间为 秒时,以P,F,E为顶点的三角形与△AED相似.
1或2.5
利用两边及夹角判定三角形相似
“相似于(∽)”和“谁和谁相似”的区别:虽然它们都表示两个图形相似,但前者对应关系固定,后者对应关系不固定(分类讨论).
两边成比例且夹角相等的两个三角形相似
课堂小结
问题1:有两边对应成比例的两个三角形相似吗?
3
3
5
5
不相似
问题2:类比三角形全等的判定方法(SAS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
角相等?
情景导入
学习目标
1.掌握相似三角形的判定定理2;(重点)
2.能熟练运用相似三角形的判定定理2.(难点)
2.改变k值的大小,再试一试。
1.画△ABC与△A'B'C',使∠A=∠A', 设法比较∠B与∠B'的大小(或∠C与∠C').△ABC和△A'B'C'相似吗?
两个三角形相似
获取新知
3.如果△ABC与△A'B'C'两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?
50°
)
4
A
B
C
3.2
2
50°
)
E
D
F
1.6
两边对应成比例且其中一边所对的角对应相等的两个三角形
不一定相似。
求证: △ABC∽△A'B'C'
A
B
C
下面我们来试着证明一下刚才的发现
A
B
C
D
E
证明:在线段A'B'(或它的延长线上)截取A'D=AB,过点D再做DE//B'C'交A'C'于点E,可得?A'DE∽?A'B'C'
∴AE'=AC,
又∵∠A'=∠A
∴?ABC≌?A'DE
∴ABC∽?A'B'C'
相似三角形判定定理2:
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
∴ABC∽?A'B'C'
符号语言:
B
A
C
B'
A'
C'
例1 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
解:∵ AE=1.5,AC=2,
∴
又∵∠EAD=∠CAB,
∴ △ADE ∽△ABC,
∴
∴
提示:
解题时要找准对应边.
例题讲解
(2)∵△ACD∽△CBD
∴∠A=∠BCD.
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°.
即∠ACB=90°.
解:(1)证明:∵CD是边AB上的高
∴∠ADC=∠CDB=90°
又CD2=AD·BD
∴
∴△ACD∽△CBD
【归纳总结】利用两边及夹角判定三角形相似的策略:
(1)角与边的联系:角是对应边的夹角,边是此对应角的两边.
一定要注意:与对应角的对边无关.
(2)找条件:已知条件中有明确的比例关系式时,只要证明与比例关系式相关的两边的夹角相等即可.
注意利用图形中的隐含条件,如:公共角、对顶角等.
C
1.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
随堂演练
2.在△ABC和△A1B1C1中,下列四个命题:
(1)若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC∶A1C1=CB∶C1B1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4 B.3 C.2 D.1
B
3、如图,给出下列条件:?
① ∠B=∠ACD;?
② ∠ADC=∠ACB;
③ ;
④ AC?=AD·AB,
其中能够判△ABC∽△ACD的有( )
A.1个 B.2个 C.3个 D.4个
C
4.如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和△ABC相似,则AQ的长为 .
5. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,
求证 △ABC ∽△AED.
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
A
B
C
D
E
思维拓展
如图,在边长为2个单位长度的正方形ABCD中,E是AB的中点,点P从点D出发沿射线DC以每秒1个单位长度的速度运动,过点P作PF⊥DE于点F,当运动时间为 秒时,以P,F,E为顶点的三角形与△AED相似.
1或2.5
利用两边及夹角判定三角形相似
“相似于(∽)”和“谁和谁相似”的区别:虽然它们都表示两个图形相似,但前者对应关系固定,后者对应关系不固定(分类讨论).
两边成比例且夹角相等的两个三角形相似
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
