4.4.3相似三角形的判别方法三---同步课件 2021-2022学年九年级数学北师大版上册(共18张ppt)
文档属性
| 名称 | 4.4.3相似三角形的判别方法三---同步课件 2021-2022学年九年级数学北师大版上册(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 934.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 15:06:12 | ||
图片预览



文档简介
4.4.3 相似三角形的判定3
1. 什么是相似三角形?在前面的课程中,我们学过哪些判定三角形相似的方法?
三角分别相等、三边成比例的两个三角形叫做相似三角形
三角形相似的判定方法有:1.两角分别相等;
2.两边成比例且夹角相等
2. 类似于判定三角形全等的SSS方法,我们能不能通过三边来判定两个三角形相似呢?
可以
知识回顾
学习目标
1. 复习已经学过的三角形相似的判定定理.
2. 掌握利用三边来判定两个三角形相似的方法,并能进
行相关计算. (重点、难点)
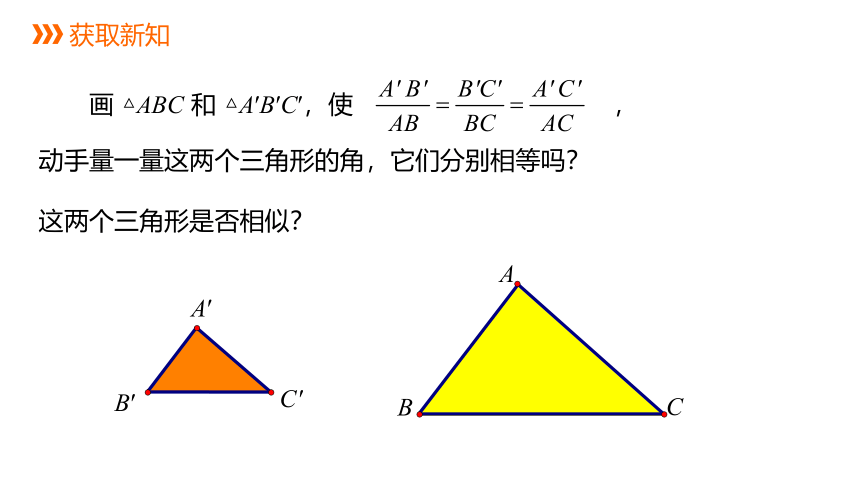
画 △ABC 和 △A′B′C′,使 ,
动手量一量这两个三角形的角,它们分别相等吗?
这两个三角形是否相似?
A
B
C
C′
B′
A′
获取新知
A
B
C
C′
B′
A′
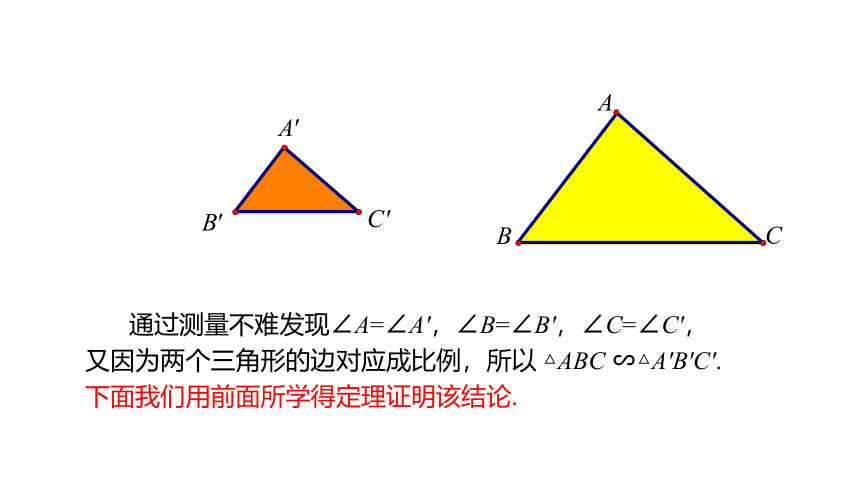
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',
又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学得定理证明该结论.
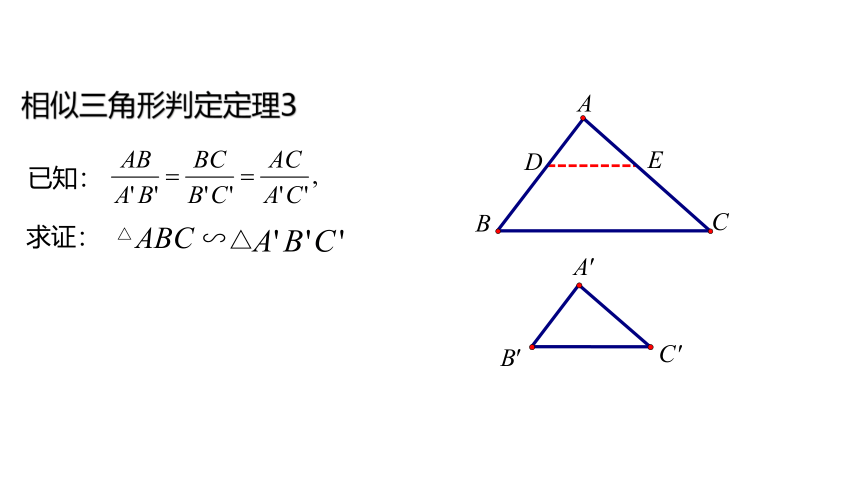
相似三角形判定定理3
求证:
已知:
∽△
△
C′
B′
A′
B
C
A
D
E
∴
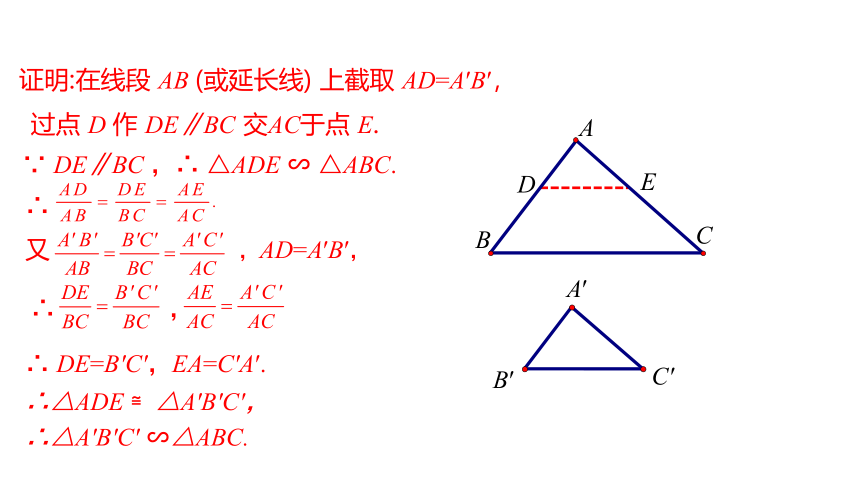
证明:在线段 AB (或延长线) 上截取 AD=A′B′,
过点 D 作 DE∥BC 交AC于点 E.
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴ DE=B′C′,EA=C′A′.
∴△ADE ≌△A′B′C′,
∴△A′B′C′ ∽△ABC.
又 ,AD=A′B′,
∴ ,
C′
B′
A′
B
C
A
D
E
相似三角形判定定理3:
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
符号语言:
∴△A'B'C'∽△ABC
∵
简记为三边对应成比例,两三角形相似。
例 如图,在 △ABC 和 △ADE 中,
∠BAD=20°,求∠CAE的度数.
∴∠BAC=∠DAE,∠BAC -∠DAC = ∠DAE -∠DAC,
即 ∠BAD=∠CAE.
∵∠BAD=20°,
∴∠CAE=20°.
∴ △ABC ∽△ADE (三边成 比例的两个三角形相似).
解:∵
例题讲解
A
B
C
D
E
归纳相似三角形的基本图形
1.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
B
随堂演练
2. 如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是 ( )
A. △PAB∽△PCA
B. △PAB∽△PDA
C. △ABC∽△DBA
D. △ABC∽△DCA
C
A
C
B
P
D
3.在△ABC中,AB=3,AC=4,在△A'B'C'中,A'B'=8,A'C'=6,
则当BC∶B'C'= 时,△A'B'C'∽ .?
1:2
△ACB
4. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA
的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
思维拓展
如图,某地四个乡镇 A,B,C,D 之间建有公路,已知 AB = 14 千米,AD = 28 千米,BD = 21 千米,DC = 31.5 千米,公路AB与 CD 平行吗?说出你的理由.
解:公路 AB 与 CD 平行.
∴
∴ △ABD∽△BDC,
∴∠ABD=∠BDC,
∴AB∥DC.
A
C
B
D
28
14
21
42
31.5
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
1. 什么是相似三角形?在前面的课程中,我们学过哪些判定三角形相似的方法?
三角分别相等、三边成比例的两个三角形叫做相似三角形
三角形相似的判定方法有:1.两角分别相等;
2.两边成比例且夹角相等
2. 类似于判定三角形全等的SSS方法,我们能不能通过三边来判定两个三角形相似呢?
可以
知识回顾
学习目标
1. 复习已经学过的三角形相似的判定定理.
2. 掌握利用三边来判定两个三角形相似的方法,并能进
行相关计算. (重点、难点)
画 △ABC 和 △A′B′C′,使 ,
动手量一量这两个三角形的角,它们分别相等吗?
这两个三角形是否相似?
A
B
C
C′
B′
A′
获取新知
A
B
C
C′
B′
A′
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',
又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学得定理证明该结论.
相似三角形判定定理3
求证:
已知:
∽△
△
C′
B′
A′
B
C
A
D
E
∴
证明:在线段 AB (或延长线) 上截取 AD=A′B′,
过点 D 作 DE∥BC 交AC于点 E.
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴ DE=B′C′,EA=C′A′.
∴△ADE ≌△A′B′C′,
∴△A′B′C′ ∽△ABC.
又 ,AD=A′B′,
∴ ,
C′
B′
A′
B
C
A
D
E
相似三角形判定定理3:
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
符号语言:
∴△A'B'C'∽△ABC
∵
简记为三边对应成比例,两三角形相似。
例 如图,在 △ABC 和 △ADE 中,
∠BAD=20°,求∠CAE的度数.
∴∠BAC=∠DAE,∠BAC -∠DAC = ∠DAE -∠DAC,
即 ∠BAD=∠CAE.
∵∠BAD=20°,
∴∠CAE=20°.
∴ △ABC ∽△ADE (三边成 比例的两个三角形相似).
解:∵
例题讲解
A
B
C
D
E
归纳相似三角形的基本图形
1.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
B
随堂演练
2. 如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是 ( )
A. △PAB∽△PCA
B. △PAB∽△PDA
C. △ABC∽△DBA
D. △ABC∽△DCA
C
A
C
B
P
D
3.在△ABC中,AB=3,AC=4,在△A'B'C'中,A'B'=8,A'C'=6,
则当BC∶B'C'= 时,△A'B'C'∽ .?
1:2
△ACB
4. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA
的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
思维拓展
如图,某地四个乡镇 A,B,C,D 之间建有公路,已知 AB = 14 千米,AD = 28 千米,BD = 21 千米,DC = 31.5 千米,公路AB与 CD 平行吗?说出你的理由.
解:公路 AB 与 CD 平行.
∴
∴ △ABD∽△BDC,
∴∠ABD=∠BDC,
∴AB∥DC.
A
C
B
D
28
14
21
42
31.5
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
