4.7.2相似三角形的周长和面积的性质 课件 2021-2022学年九年级数学北师大版上册(共18张ppt)
文档属性
| 名称 | 4.7.2相似三角形的周长和面积的性质 课件 2021-2022学年九年级数学北师大版上册(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 204.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 15:17:16 | ||
图片预览






文档简介
4.7.2 相似三角形周长和面积的性质
我们知道,如果两个三角形相似,它们对应高的比、对应中线的比和对应角平分线的比都等于相似比.那么它们周长的比之间有什么关系?也等于相似比吗?面积之比呢?
A
B
C
A1
B1
C1
情景导入
学习目标
1.理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.(重点)
2.掌握相似三角形的周长比、面积比在实际中的应用.(难点)
一、相似三角形的周长比等于相似比
归纳:相似三角形的周长比等于相似比。
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=_____
(2)与(1)的周长比=_____
(3)与(1)的相似比=_____
(3)与(1)的周长比=_____
2:1
2:1
3:1
3:1
从上面可以看出当相似比=k时,周长比=______
k
获取新知
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
二、相似三角形的面积比等于相似比的平方
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似
(2)与(1)的相似比=_______,
(2)与(1)的面积比=_______;
(3)与(1)的相似比=_______,
(3)与(1)的面积比=_______.
4:1
3:1
9:1
2:1
归纳:相似三角形的面积比等于相似比的平方。
从上面可以看出当相似比=k时,面积比=______
k2
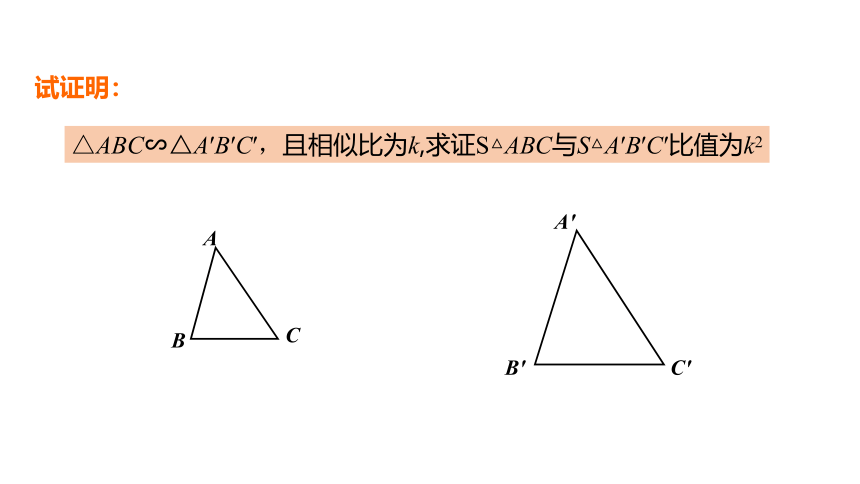
试证明:
△ABC∽△A′B′C′,且相似比为k,求证S△ABC与S△A′B′C′比值为k2
A
B
C
A′
B′
C′
证明:设△ABC∽△A′B′C′,相似比为k,
如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′.
∵△ABC∽△A′B′C′.
A
B
C
A′
B′
C′
D
D′
例 如图,将△ABC沿BC方向平移得到△DEF,△ABC与 △DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC(两角分别相等的两个三角形相似).
例题讲解
(相似三角形的面积比等于相似比的平方),
∴EC2=2.
∴EC=
∴BE=BC-EC=2-
即△ABC平移的距离为2-
1、两个相似三角形对应边比为3:5,那么相似比为 ,
周长比为 ,面积比为 .
3:5
9:25
3:5
随堂演练
2、把 一个三角形变成和它相似的三角形,则如果边长扩大为原来的100倍,那么面积扩大为原来的___________倍;
如果面积扩大为原来的100倍,那么边长扩大为原来的________倍。
10000
10
3、已知△ABC∽△A′B′C′,AC: A′ C′=4:3。
(1)若△ABC的周长为24cm,则△A′B′C′的周长为 cm;
(2)若△ABC的面积为32 cm2 ,则△A′B′C′的面积为 cm2
18
18
4、已知,在△ABC 中,DE//BC, DE:BC=3:5 ,则
(1)AD:DB= ;
(2)△ADE的面积:梯形DECB的面积= ;
(3)△ABC的面积为25,则△ADE的面积=_________.
3:2
9:16
9
5.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
相似
相似比为2:1
面积比为4:1
6、如图,已知DE∥BC,BD=3AD,S△ABC =48,求:△ADE的面积。
解:∵ DE∥BC
∴∠ADE=∠ABC, ∠AED=∠ACB
∴△ADE ∽△ABC
又∵BD=3AD
可得相似比k=AD:AB=1:2
∴S△ADE =1/4 S△ABC =12
如图,这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米, 则地面上阴影部分的面积约为多少 (结果保留两位小数)?
思维拓展
解:∵ FH = 1 米,AH = 3 米,
桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,
∴△ADF ∽△ACH,
A
D
E
F
C
B
H
∴ 即
解得 CH = 0.9米.
∴ 阴影部分的面积为:
答:地面上阴影部分的面积为 2.54 平方米.
(平方米).
A
D
E
F
C
B
H
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
课堂小结
我们知道,如果两个三角形相似,它们对应高的比、对应中线的比和对应角平分线的比都等于相似比.那么它们周长的比之间有什么关系?也等于相似比吗?面积之比呢?
A
B
C
A1
B1
C1
情景导入
学习目标
1.理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.(重点)
2.掌握相似三角形的周长比、面积比在实际中的应用.(难点)
一、相似三角形的周长比等于相似比
归纳:相似三角形的周长比等于相似比。
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=_____
(2)与(1)的周长比=_____
(3)与(1)的相似比=_____
(3)与(1)的周长比=_____
2:1
2:1
3:1
3:1
从上面可以看出当相似比=k时,周长比=______
k
获取新知
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
二、相似三角形的面积比等于相似比的平方
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似
(2)与(1)的相似比=_______,
(2)与(1)的面积比=_______;
(3)与(1)的相似比=_______,
(3)与(1)的面积比=_______.
4:1
3:1
9:1
2:1
归纳:相似三角形的面积比等于相似比的平方。
从上面可以看出当相似比=k时,面积比=______
k2
试证明:
△ABC∽△A′B′C′,且相似比为k,求证S△ABC与S△A′B′C′比值为k2
A
B
C
A′
B′
C′
证明:设△ABC∽△A′B′C′,相似比为k,
如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′.
∵△ABC∽△A′B′C′.
A
B
C
A′
B′
C′
D
D′
例 如图,将△ABC沿BC方向平移得到△DEF,△ABC与 △DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC(两角分别相等的两个三角形相似).
例题讲解
(相似三角形的面积比等于相似比的平方),
∴EC2=2.
∴EC=
∴BE=BC-EC=2-
即△ABC平移的距离为2-
1、两个相似三角形对应边比为3:5,那么相似比为 ,
周长比为 ,面积比为 .
3:5
9:25
3:5
随堂演练
2、把 一个三角形变成和它相似的三角形,则如果边长扩大为原来的100倍,那么面积扩大为原来的___________倍;
如果面积扩大为原来的100倍,那么边长扩大为原来的________倍。
10000
10
3、已知△ABC∽△A′B′C′,AC: A′ C′=4:3。
(1)若△ABC的周长为24cm,则△A′B′C′的周长为 cm;
(2)若△ABC的面积为32 cm2 ,则△A′B′C′的面积为 cm2
18
18
4、已知,在△ABC 中,DE//BC, DE:BC=3:5 ,则
(1)AD:DB= ;
(2)△ADE的面积:梯形DECB的面积= ;
(3)△ABC的面积为25,则△ADE的面积=_________.
3:2
9:16
9
5.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
相似
相似比为2:1
面积比为4:1
6、如图,已知DE∥BC,BD=3AD,S△ABC =48,求:△ADE的面积。
解:∵ DE∥BC
∴∠ADE=∠ABC, ∠AED=∠ACB
∴△ADE ∽△ABC
又∵BD=3AD
可得相似比k=AD:AB=1:2
∴S△ADE =1/4 S△ABC =12
如图,这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米, 则地面上阴影部分的面积约为多少 (结果保留两位小数)?
思维拓展
解:∵ FH = 1 米,AH = 3 米,
桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,
∴△ADF ∽△ACH,
A
D
E
F
C
B
H
∴ 即
解得 CH = 0.9米.
∴ 阴影部分的面积为:
答:地面上阴影部分的面积为 2.54 平方米.
(平方米).
A
D
E
F
C
B
H
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
