2021-2022学年九年级数学北师大版上册6.1反比例函数 课件(22张PPT)
文档属性
| 名称 | 2021-2022学年九年级数学北师大版上册6.1反比例函数 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 21:05:48 | ||
图片预览







文档简介
6.1 反比例函数
在过去的学习中我们学习了哪些函数?
一次函数
y=2x-6
y=3x
正比例函数是一次函数的特殊化
知识回顾
点击视频欣赏南昌赣江两岸灯光秀,灯光忽明忽暗一会黑夜,一会白天,十分绚丽,产生这样炫酷的效果是什么原因呢?能用我们学习的知识解决吗?
情景引入
学习目标
1. 理解并掌握反比例函数的概念. (重点)
2. 从实际问题中抽象出反比例函数的概念,能根据
已知条件确定反比例函数的解析式. (重点、难点)
京沪线铁路全程为1318km,某次列车平速度v(单位:km/h)随此次列车的全程运行时间t(单位:h)的变化而变化.则vt=________,用t表示v的函数表达式为________.
1318
获取新知
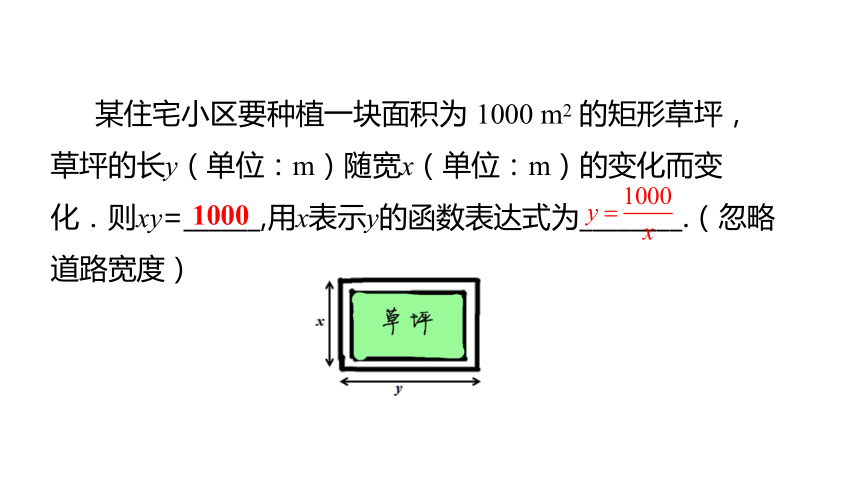
某住宅小区要种植一块面积为 1000 m2 的矩形草坪,草坪的长y(单位:m)随宽x(单位:m)的变化而变化.则xy=______,用x表示y的函数表达式为________.(忽略道路宽度)
1000
反比例函数概念
观察上面各函数关系式有什么特点,完成下面填空.
都具有 的形式,其中 是常数.
分式
分子
反比例函数的自变量 x ≠0.
一般地,如果两个变量x,y之间的对应关系可以表示成 (k为常数,k≠0)的形式,那么称y是x的反比例函数。
例1 下列哪些关系式中的y是x的反比例函数,如果是请指出k的值.
是,k=-3
不是,y=2x
是,k=
是,k=3
不是
例题讲解
补充:反比例函数的表达形式:
① (k≠0)
②xy=k(k≠0)
③y=kx-1(k≠0)
x≠0,y≠0
反比例函数:
k≠0 即a+1≠0
自变量指数为-1 即
解:由题可知a+1≠0且
得a=1
总结:利用反比例概念求字母值时一定注意k≠0且自变量指数为-1
例2 已知函数 是反比例函数,求a的值
例3 已知y与x成反比例,并且当x=2时,y=6.
(1)写出y和x之间的函数关式;
(1)求当x=4时y的值.
解:(1)设
∵当x=2时y=6,
∴ ,解得k=12, 因此
(2)当x=4时,
归纳总结
用待定系数法确定反比例函数的表达式的一般步骤
二 代
三 求
四 写
一 设
设反比例函数
将一对对应的x,y值带入函数,得到关于k的方程
解方程求待定系数k
写出反比例函数表达式
用待定系数法求反比例函数解析式,只需x,y的一对值即可,k ≠ 0.
例4 用反比例函数表达式表示下列问题中两个变量间的对应关系:
(1)小明完成100 m赛跑时,所用时间t(s)随他跑步的平均速度v(m/s)的变化而变化;
(2)一个密闭容器内有气体0.5 kg,气体的密度ρ(kg/m3)随容器体积V(m3)的变化而变化;
(3)压力为600 N时,压强P随受力面积S的变化而变化;
(4)三角形的面积为20,它的底边a上的高h随底边a的变化而变化.
解:(1)∵vt=100,∴t= (v>0);
(2)∵0.5=ρV,∴ρ= (V>0);
(3)∵PS=600,∴P= (S>0);
(4)∵ ah=20,∴h= (a>0).
分析:先根据每个问题中两个变量与已知量之间的等量关系列出等式,然后通过变形得到函数表达式.
1. 下列函数中,y是x的反比例函数的是( )
A
A. B.
C. D.
随堂演练
2. 生活中有许多反比例函数的例子,在下面的实例中,x 和 y 成反比例函数关系的有 ( )
① x人共饮水10 kg,平均每人饮水 y kg;②底面半径为 x m,高为 y m的圆柱形水桶的体积为10 m3;③用铁丝做一个圆,铁丝的长为 x cm,做成圆的半径为 y cm;④在水龙头前放满一桶水,出水的速度为 x,放满一桶水的时间 y
A. 1个 B. 2个 C. 3个 D. 4个
B
3. 填空
(1) 若 是反比例函数,则 m 的取值范围是 .
(2) 若 是反比例函数,则m的取值范围是 .
(3) 若 是反比例函数,则m的取值范围是 .
m ≠ 1
m ≠ 0且m ≠ -2
m = -1
4.如图所示,已知菱形 ABCD 的面积为180,设它的两条对角线 AC,BD的长分别为x,y. 写出变量 y与 x 之间的关系式,并指出它是什么函数.
解:∵菱形的面积等于两条对角线长乘积的一半
∴
∴变量 y与 x 之间的关系式为
∴它是反比例函数.
A
B
C
D
已知 y = y1+y2,y1与 (x-1)成正比例,y2 与 (x + 1) 成反比例,当 x = 0 时,y =-3;当 x =1 时,y = -1,求:
(1) y 关于 x 的关系式;
(2) 当 x = 时,y 的值.
思维拓展
解:(1)设 y1 = k1(x-1) (k1≠0), (k2≠0),
则
∵ x = 0 时,y =-3;x =1 时,y = -1
∴
∴k1=1,k2=-2.
∴
-3=-k1+k2 ,
(2)把 x = 代入 (1) 中函数关系式,得 y =
建立反比例函数模型
关键:等量关系
用待定系数法求反比例函数解析式
步骤:设-代-求-写
反比例函数:定义有三种表达方式
(k为常数且k≠0)
反比例函数
课堂小结
在过去的学习中我们学习了哪些函数?
一次函数
y=2x-6
y=3x
正比例函数是一次函数的特殊化
知识回顾
点击视频欣赏南昌赣江两岸灯光秀,灯光忽明忽暗一会黑夜,一会白天,十分绚丽,产生这样炫酷的效果是什么原因呢?能用我们学习的知识解决吗?
情景引入
学习目标
1. 理解并掌握反比例函数的概念. (重点)
2. 从实际问题中抽象出反比例函数的概念,能根据
已知条件确定反比例函数的解析式. (重点、难点)
京沪线铁路全程为1318km,某次列车平速度v(单位:km/h)随此次列车的全程运行时间t(单位:h)的变化而变化.则vt=________,用t表示v的函数表达式为________.
1318
获取新知
某住宅小区要种植一块面积为 1000 m2 的矩形草坪,草坪的长y(单位:m)随宽x(单位:m)的变化而变化.则xy=______,用x表示y的函数表达式为________.(忽略道路宽度)
1000
反比例函数概念
观察上面各函数关系式有什么特点,完成下面填空.
都具有 的形式,其中 是常数.
分式
分子
反比例函数的自变量 x ≠0.
一般地,如果两个变量x,y之间的对应关系可以表示成 (k为常数,k≠0)的形式,那么称y是x的反比例函数。
例1 下列哪些关系式中的y是x的反比例函数,如果是请指出k的值.
是,k=-3
不是,y=2x
是,k=
是,k=3
不是
例题讲解
补充:反比例函数的表达形式:
① (k≠0)
②xy=k(k≠0)
③y=kx-1(k≠0)
x≠0,y≠0
反比例函数:
k≠0 即a+1≠0
自变量指数为-1 即
解:由题可知a+1≠0且
得a=1
总结:利用反比例概念求字母值时一定注意k≠0且自变量指数为-1
例2 已知函数 是反比例函数,求a的值
例3 已知y与x成反比例,并且当x=2时,y=6.
(1)写出y和x之间的函数关式;
(1)求当x=4时y的值.
解:(1)设
∵当x=2时y=6,
∴ ,解得k=12, 因此
(2)当x=4时,
归纳总结
用待定系数法确定反比例函数的表达式的一般步骤
二 代
三 求
四 写
一 设
设反比例函数
将一对对应的x,y值带入函数,得到关于k的方程
解方程求待定系数k
写出反比例函数表达式
用待定系数法求反比例函数解析式,只需x,y的一对值即可,k ≠ 0.
例4 用反比例函数表达式表示下列问题中两个变量间的对应关系:
(1)小明完成100 m赛跑时,所用时间t(s)随他跑步的平均速度v(m/s)的变化而变化;
(2)一个密闭容器内有气体0.5 kg,气体的密度ρ(kg/m3)随容器体积V(m3)的变化而变化;
(3)压力为600 N时,压强P随受力面积S的变化而变化;
(4)三角形的面积为20,它的底边a上的高h随底边a的变化而变化.
解:(1)∵vt=100,∴t= (v>0);
(2)∵0.5=ρV,∴ρ= (V>0);
(3)∵PS=600,∴P= (S>0);
(4)∵ ah=20,∴h= (a>0).
分析:先根据每个问题中两个变量与已知量之间的等量关系列出等式,然后通过变形得到函数表达式.
1. 下列函数中,y是x的反比例函数的是( )
A
A. B.
C. D.
随堂演练
2. 生活中有许多反比例函数的例子,在下面的实例中,x 和 y 成反比例函数关系的有 ( )
① x人共饮水10 kg,平均每人饮水 y kg;②底面半径为 x m,高为 y m的圆柱形水桶的体积为10 m3;③用铁丝做一个圆,铁丝的长为 x cm,做成圆的半径为 y cm;④在水龙头前放满一桶水,出水的速度为 x,放满一桶水的时间 y
A. 1个 B. 2个 C. 3个 D. 4个
B
3. 填空
(1) 若 是反比例函数,则 m 的取值范围是 .
(2) 若 是反比例函数,则m的取值范围是 .
(3) 若 是反比例函数,则m的取值范围是 .
m ≠ 1
m ≠ 0且m ≠ -2
m = -1
4.如图所示,已知菱形 ABCD 的面积为180,设它的两条对角线 AC,BD的长分别为x,y. 写出变量 y与 x 之间的关系式,并指出它是什么函数.
解:∵菱形的面积等于两条对角线长乘积的一半
∴
∴变量 y与 x 之间的关系式为
∴它是反比例函数.
A
B
C
D
已知 y = y1+y2,y1与 (x-1)成正比例,y2 与 (x + 1) 成反比例,当 x = 0 时,y =-3;当 x =1 时,y = -1,求:
(1) y 关于 x 的关系式;
(2) 当 x = 时,y 的值.
思维拓展
解:(1)设 y1 = k1(x-1) (k1≠0), (k2≠0),
则
∵ x = 0 时,y =-3;x =1 时,y = -1
∴
∴k1=1,k2=-2.
∴
-3=-k1+k2 ,
(2)把 x = 代入 (1) 中函数关系式,得 y =
建立反比例函数模型
关键:等量关系
用待定系数法求反比例函数解析式
步骤:设-代-求-写
反比例函数:定义有三种表达方式
(k为常数且k≠0)
反比例函数
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
