2021-2022学年九年级数学北师大版上册6.2 第1课时反比例函数的图象 课件(21张PPT)
文档属性
| 名称 | 2021-2022学年九年级数学北师大版上册6.2 第1课时反比例函数的图象 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览




文档简介
6.2.1 反比例函数的图像
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
(2)xy = k.
(3)x和y均不会取0.
知识回顾
3. 如何画一次函数的图象?
列
表
描
点
连
线
一般地,形如 y= (k是常数, k ≠0)的函数叫做反比例函数.
学习目标
1.会用描点法画出反比例函数的图象,并掌握反比例函数图象的特征.(重点)
2.会利用反比例函数图象解决相关问题.(难点)
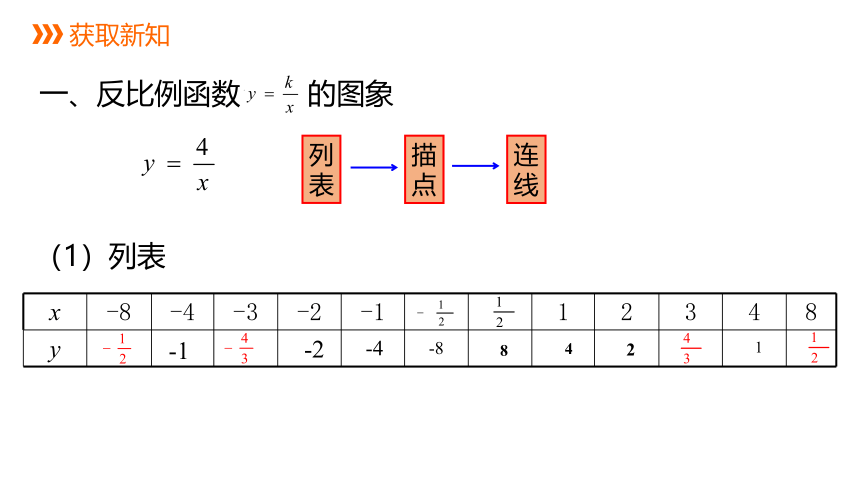
(1)列表
列
表
描
点
连
线
x
-8
-4
-3
-2
-1
1
2
3
4
8
y
-1
-2
-4
-8
8
4
2
1
一、反比例函数 的图象
获取新知
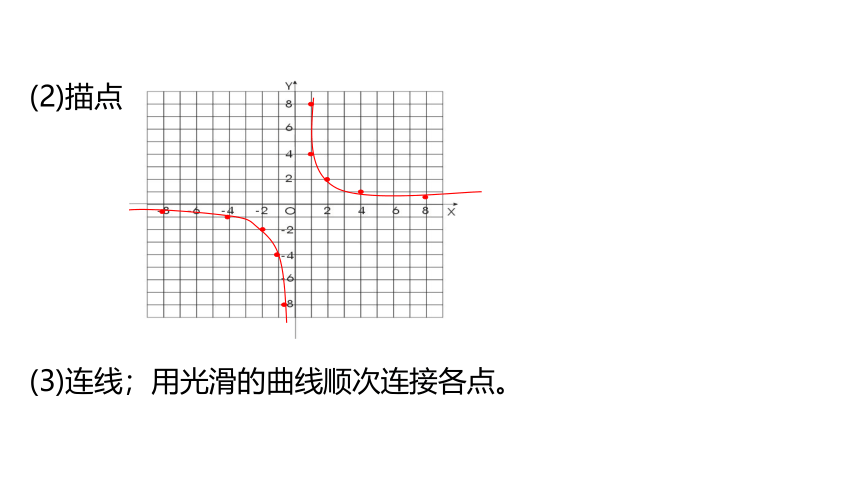
(2)描点
(3)连线;用光滑的曲线顺次连接各点。
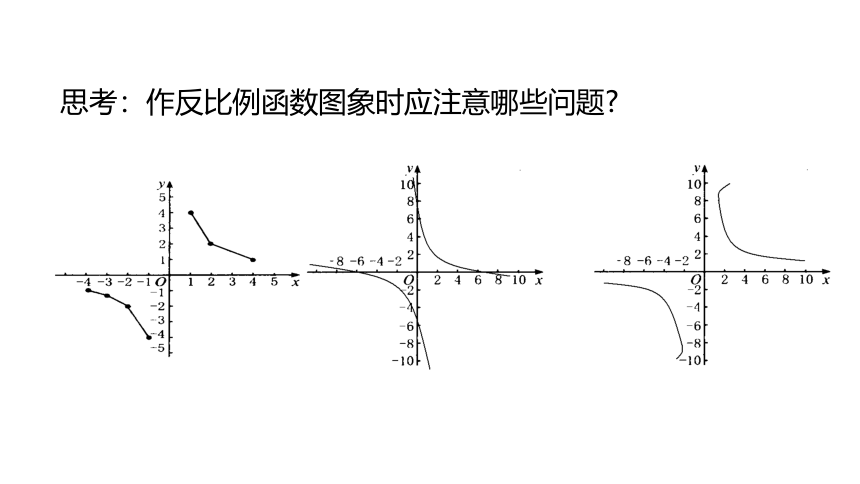
思考:作反比例函数图象时应注意哪些问题?
注意问题:
①列表:自变量的值可以选取一些互为相反数的一对一对的数,这样既可简化计算,又便于对称性描点,要注意到自变量的取值应使函数有意义(即x≠0)。
②描点:一般情况下所选的点越多则图象越精确;
③连线:用平滑的曲线连接各点,得到反比例函数的图象。
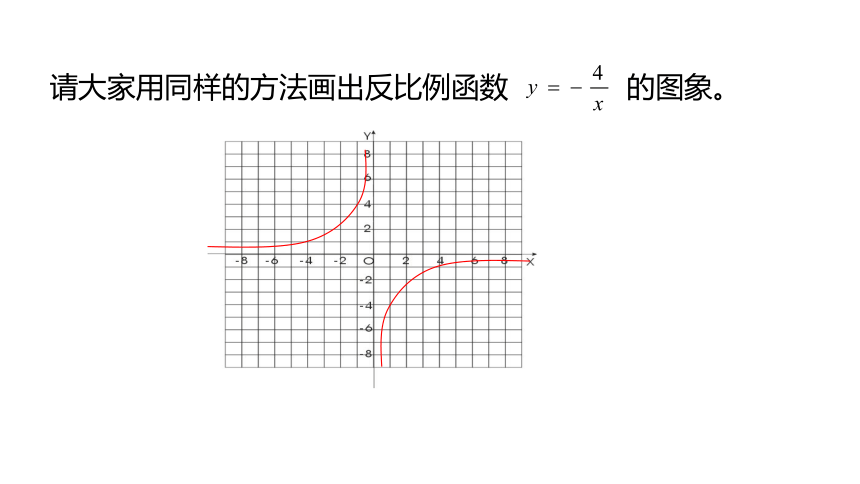
请大家用同样的方法画出反比例函数 的图象。
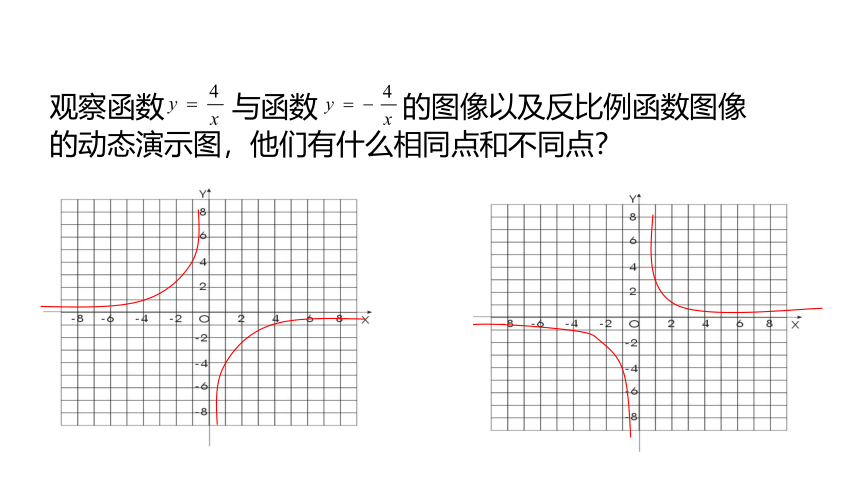
观察函数 与函数 的图像以及反比例函数图像的动态演示图,他们有什么相同点和不同点?
动态演示图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
函数图像
相同点
不同点
1.都有两支曲线
2.图象自身关于原点成中心对称;
3.图象自身是轴对称图形;
对称轴为y=x和y=-x
图像在一、三象限
图像在二、四象限
总结
形状:反比例函数 的图像由两只曲线组成,
因此称反比例函数 的图像为双曲线。
位置:由k决定
当k>0时,两支曲线分别位于一、三象限内;
当k<0时,两支曲线分别位于二、四象限内。
例1 若双曲线y= 的两个分支分别在第二、四象限,则k 的取值范围是( )
A. k> B. k<
C. k= D.不存在
B
例题讲解
解析:反比例函数图象的两个分支分别在第二、四象限,则必有2k-1<0,解得k< .故选B.
例2 如图所示的曲线是函数 (m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
x
y
O
解:(1)由题意可得,m-5>0,
解得m>5.
(2) ∵两个函数的交点为A(2,n),
∴ , 解得 .
∴ 点A的坐标为(2,4)
∴反比例函数的解析式为 .
1.已知反比例函数 ,则其图象在平面直角坐标系中可能是( )
C
随堂演练
2.已知某种品牌电脑的显示器的寿命大约为2×104时,这种显示器工作的天数为d(天),平均每天工作的时间为t(时),那么能正确表示d与t之间的函数关系图象的是( )
C
3.如图,已知直线y=k1x(k1≠0)与反比例函数 (k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(-1,-2) B.(-1,2)
C.(1,-2) D.(-2,-1)
A
4、如果点(1,-2)在双曲线 上,那么该双曲线在第
象限.
5、如果反比例函数 的图象位于第二、四象限内,那么满足条件的正整数k的值是 .
二、四
k<3
6. 已知反比例函数 (k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的表达式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由.
解:(1)∵反比例函数 (k为常数,k≠0)的图象经过点 A(2,3),
∴把点A的坐标代入表达式,得 ,解得k=6,
∴这个函数的表达式为
(2)∵反比例函数的表达式为 ,
∴ 6=xy
分别把点B,C的坐标代入,
得(-1)×6=-6≠6,则点B不在该函数图象上;
3×2=6,则点C在该函数图象上.
反比例函数
的图象
形状
双曲线
位置
对称性
当k>0时,两支曲线分别位于
第一、三象限内
当k<0时,两支曲线分别位于
第二、四象限内
中心对称:原点O为对称中心;
轴对称:对称轴为直线y=x和y=-x
课堂小结
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
(2)xy = k.
(3)x和y均不会取0.
知识回顾
3. 如何画一次函数的图象?
列
表
描
点
连
线
一般地,形如 y= (k是常数, k ≠0)的函数叫做反比例函数.
学习目标
1.会用描点法画出反比例函数的图象,并掌握反比例函数图象的特征.(重点)
2.会利用反比例函数图象解决相关问题.(难点)
(1)列表
列
表
描
点
连
线
x
-8
-4
-3
-2
-1
1
2
3
4
8
y
-1
-2
-4
-8
8
4
2
1
一、反比例函数 的图象
获取新知
(2)描点
(3)连线;用光滑的曲线顺次连接各点。
思考:作反比例函数图象时应注意哪些问题?
注意问题:
①列表:自变量的值可以选取一些互为相反数的一对一对的数,这样既可简化计算,又便于对称性描点,要注意到自变量的取值应使函数有意义(即x≠0)。
②描点:一般情况下所选的点越多则图象越精确;
③连线:用平滑的曲线连接各点,得到反比例函数的图象。
请大家用同样的方法画出反比例函数 的图象。
观察函数 与函数 的图像以及反比例函数图像的动态演示图,他们有什么相同点和不同点?
动态演示图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
函数图像
相同点
不同点
1.都有两支曲线
2.图象自身关于原点成中心对称;
3.图象自身是轴对称图形;
对称轴为y=x和y=-x
图像在一、三象限
图像在二、四象限
总结
形状:反比例函数 的图像由两只曲线组成,
因此称反比例函数 的图像为双曲线。
位置:由k决定
当k>0时,两支曲线分别位于一、三象限内;
当k<0时,两支曲线分别位于二、四象限内。
例1 若双曲线y= 的两个分支分别在第二、四象限,则k 的取值范围是( )
A. k> B. k<
C. k= D.不存在
B
例题讲解
解析:反比例函数图象的两个分支分别在第二、四象限,则必有2k-1<0,解得k< .故选B.
例2 如图所示的曲线是函数 (m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
x
y
O
解:(1)由题意可得,m-5>0,
解得m>5.
(2) ∵两个函数的交点为A(2,n),
∴ , 解得 .
∴ 点A的坐标为(2,4)
∴反比例函数的解析式为 .
1.已知反比例函数 ,则其图象在平面直角坐标系中可能是( )
C
随堂演练
2.已知某种品牌电脑的显示器的寿命大约为2×104时,这种显示器工作的天数为d(天),平均每天工作的时间为t(时),那么能正确表示d与t之间的函数关系图象的是( )
C
3.如图,已知直线y=k1x(k1≠0)与反比例函数 (k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(-1,-2) B.(-1,2)
C.(1,-2) D.(-2,-1)
A
4、如果点(1,-2)在双曲线 上,那么该双曲线在第
象限.
5、如果反比例函数 的图象位于第二、四象限内,那么满足条件的正整数k的值是 .
二、四
k<3
6. 已知反比例函数 (k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的表达式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由.
解:(1)∵反比例函数 (k为常数,k≠0)的图象经过点 A(2,3),
∴把点A的坐标代入表达式,得 ,解得k=6,
∴这个函数的表达式为
(2)∵反比例函数的表达式为 ,
∴ 6=xy
分别把点B,C的坐标代入,
得(-1)×6=-6≠6,则点B不在该函数图象上;
3×2=6,则点C在该函数图象上.
反比例函数
的图象
形状
双曲线
位置
对称性
当k>0时,两支曲线分别位于
第一、三象限内
当k<0时,两支曲线分别位于
第二、四象限内
中心对称:原点O为对称中心;
轴对称:对称轴为直线y=x和y=-x
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
