第七章 《三角形》复习与小结
文档属性
| 名称 | 第七章 《三角形》复习与小结 |
|
|
| 格式 | zip | ||
| 文件大小 | 37.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览


文档简介
第七章 三角形 复习与小结
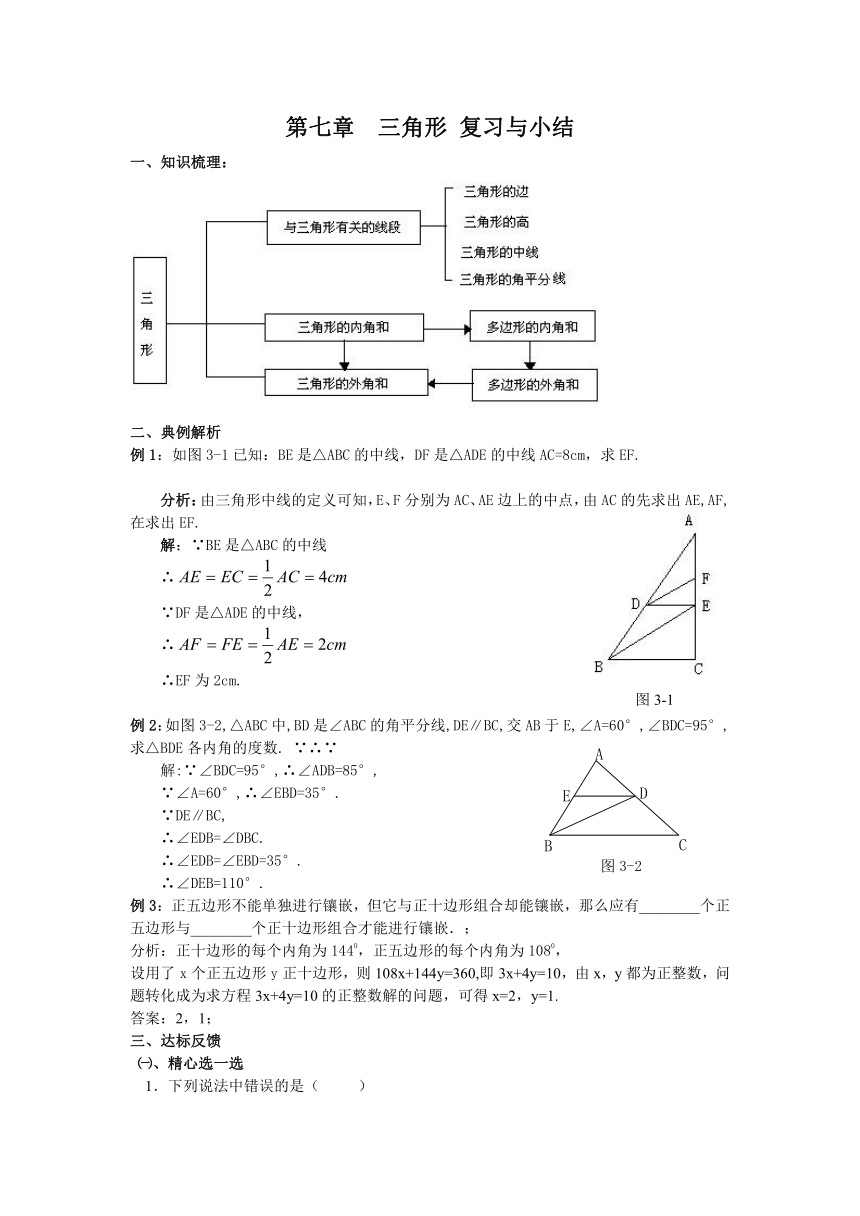
一、知识梳理:
二、典例解析
例1:如图3-1已知:BE是△ABC的中线,DF是△ADE的中线AC=8cm,求EF.
分析:由三角形中线的定义可知,E、F分别为AC、AE边上的中点,由AC的先求出AE,AF,在求出EF.
解:∵BE是△ABC的中线
∴
∵DF是△ADE的中线,
∴
∴EF为2cm.
例2:如图3-2,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,求△BDE各内角的度数. ∵∴∵
解:∵∠BDC=95°,∴∠ADB=85°,
∵∠A=60°,∴∠EBD=35°.
∵DE∥BC,
∴∠EDB=∠DBC.
∴∠EDB=∠EBD=35°.
∴∠DEB=110°.
例3:正五边形不能单独进行镶嵌,但它与正十边形组合却能镶嵌,那么应有________个正五边形与________个正十边形组合才能进行镶嵌.;
分析:正十边形的每个内角为1440,正五边形的每个内角为1080,
设用了x个正五边形y正十边形,则108x+144y=360,即3x+4y=10,由x,y都为正整数,问题转化成为求方程3x+4y=10的正整数解的问题,可得x=2,y=1.
答案:2,1;
三、达标反馈
㈠、精心选一选
1.下列说法中错误的是( )
A.三角形三条角平分线都在三角形的内部B.三角形的三条中线都在三角形的内部
C.三角形的三条高都在三角形的内部 D.三角形三条高至少有一条在三角形的内部
2.能把一个三角形分成两个面积相等的三角形是( )
A.中线 B.高 C.角平分线 D.以上都不是
3.等腰三角形的两边分别长7cm和13cm,则它的周长是( )
A.27cm B.33cm C.27cm或33cm D.以上结论都不对
4.△ABC中,∠A=2∠B=3∠C,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.含30°角的直角三角形
5.下列说法中正确的是 ( )
A.三角形的外角中至少有两个锐角 B.三角形的外角中至少有两个钝角
C.三角形的内角中至少有一个直角 D.三角形的内角中至少有一个钝角
6. 一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360° B.外角和增加360° C.对角线增加一条 D.内角和增加180°
7.一个多边形只有27条对角线,则这个多边形的边数为( )
(A)8 (B)9 (C)10 (D)11
8.下列正多边形中,与正三角形同时使用,能进行镶嵌的是( )
A.正十二边形 B.正十边形 C.正八边形 D.正五边形
9.△ABC中,cm,cm, c=14cm,则x的取值范围是 ( )
A. B. C. D.
10.锐角三角形的三个内角是∠A、∠B、∠C,如果,,,那么、、这三个角中( )
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
㈡、细心填一填
1.如图所示,图中的∠1=______________ .
2.如果三条线段a、b、c,可组成三角形,且a=3,b=5,c是偶数,则c的值为 .
3.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在位置,A点落在位置,若AC⊥,则∠BAC的度数是__________
4.如果一个多边形的每一个外角都小于45 这样的多边形边数的最小值是_______.
5.一个直角三角形两锐角的平分线所夹的钝角为 .
6.一个多边形的每一个外角都等于36,则该多边形的内角和等于
7.如①图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角有________个.
8.如图 ②,△ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF =_________度.
① ②
㈢、耐心解一解
1.如图,一块模板中AB、CD的延长线相交成80°角,因交点不在板上,不便测量,工人师傅连结AC,测得∠BAC=34°∠DCA=65°,此时,AB、CD的延长线相交成的角是否符合规定?为什么?
2.如图,在△ABC中,D在BC的延长线上,E在CA的延长线上,F在AB上,试比较∠1与∠2的大小.
3.两个正多边形的边数之比为1∶2,内角和之比为3∶8,求这两个多边形的边数、内角和.
4.在△ABC中AB=AC,AC上的中线BD把三角形的周长分为24cm和30cm的两个部分,求三角形的三边长.
5.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.
6.如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.求∠ADE的度数.
图3-1
图3-2
E
A
C
D
B
F
1
2
一、知识梳理:
二、典例解析
例1:如图3-1已知:BE是△ABC的中线,DF是△ADE的中线AC=8cm,求EF.
分析:由三角形中线的定义可知,E、F分别为AC、AE边上的中点,由AC的先求出AE,AF,在求出EF.
解:∵BE是△ABC的中线
∴
∵DF是△ADE的中线,
∴
∴EF为2cm.
例2:如图3-2,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,求△BDE各内角的度数. ∵∴∵
解:∵∠BDC=95°,∴∠ADB=85°,
∵∠A=60°,∴∠EBD=35°.
∵DE∥BC,
∴∠EDB=∠DBC.
∴∠EDB=∠EBD=35°.
∴∠DEB=110°.
例3:正五边形不能单独进行镶嵌,但它与正十边形组合却能镶嵌,那么应有________个正五边形与________个正十边形组合才能进行镶嵌.;
分析:正十边形的每个内角为1440,正五边形的每个内角为1080,
设用了x个正五边形y正十边形,则108x+144y=360,即3x+4y=10,由x,y都为正整数,问题转化成为求方程3x+4y=10的正整数解的问题,可得x=2,y=1.
答案:2,1;
三、达标反馈
㈠、精心选一选
1.下列说法中错误的是( )
A.三角形三条角平分线都在三角形的内部B.三角形的三条中线都在三角形的内部
C.三角形的三条高都在三角形的内部 D.三角形三条高至少有一条在三角形的内部
2.能把一个三角形分成两个面积相等的三角形是( )
A.中线 B.高 C.角平分线 D.以上都不是
3.等腰三角形的两边分别长7cm和13cm,则它的周长是( )
A.27cm B.33cm C.27cm或33cm D.以上结论都不对
4.△ABC中,∠A=2∠B=3∠C,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.含30°角的直角三角形
5.下列说法中正确的是 ( )
A.三角形的外角中至少有两个锐角 B.三角形的外角中至少有两个钝角
C.三角形的内角中至少有一个直角 D.三角形的内角中至少有一个钝角
6. 一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360° B.外角和增加360° C.对角线增加一条 D.内角和增加180°
7.一个多边形只有27条对角线,则这个多边形的边数为( )
(A)8 (B)9 (C)10 (D)11
8.下列正多边形中,与正三角形同时使用,能进行镶嵌的是( )
A.正十二边形 B.正十边形 C.正八边形 D.正五边形
9.△ABC中,cm,cm, c=14cm,则x的取值范围是 ( )
A. B. C. D.
10.锐角三角形的三个内角是∠A、∠B、∠C,如果,,,那么、、这三个角中( )
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
㈡、细心填一填
1.如图所示,图中的∠1=______________ .
2.如果三条线段a、b、c,可组成三角形,且a=3,b=5,c是偶数,则c的值为 .
3.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在位置,A点落在位置,若AC⊥,则∠BAC的度数是__________
4.如果一个多边形的每一个外角都小于45 这样的多边形边数的最小值是_______.
5.一个直角三角形两锐角的平分线所夹的钝角为 .
6.一个多边形的每一个外角都等于36,则该多边形的内角和等于
7.如①图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角有________个.
8.如图 ②,△ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF =_________度.
① ②
㈢、耐心解一解
1.如图,一块模板中AB、CD的延长线相交成80°角,因交点不在板上,不便测量,工人师傅连结AC,测得∠BAC=34°∠DCA=65°,此时,AB、CD的延长线相交成的角是否符合规定?为什么?
2.如图,在△ABC中,D在BC的延长线上,E在CA的延长线上,F在AB上,试比较∠1与∠2的大小.
3.两个正多边形的边数之比为1∶2,内角和之比为3∶8,求这两个多边形的边数、内角和.
4.在△ABC中AB=AC,AC上的中线BD把三角形的周长分为24cm和30cm的两个部分,求三角形的三边长.
5.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.
6.如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.求∠ADE的度数.
图3-1
图3-2
E
A
C
D
B
F
1
2
