第八章《二元一次方程组》复习与小结
文档属性
| 名称 | 第八章《二元一次方程组》复习与小结 |
|
|
| 格式 | zip | ||
| 文件大小 | 46.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览


文档简介
第八章《二元一次方程组》复习与小结
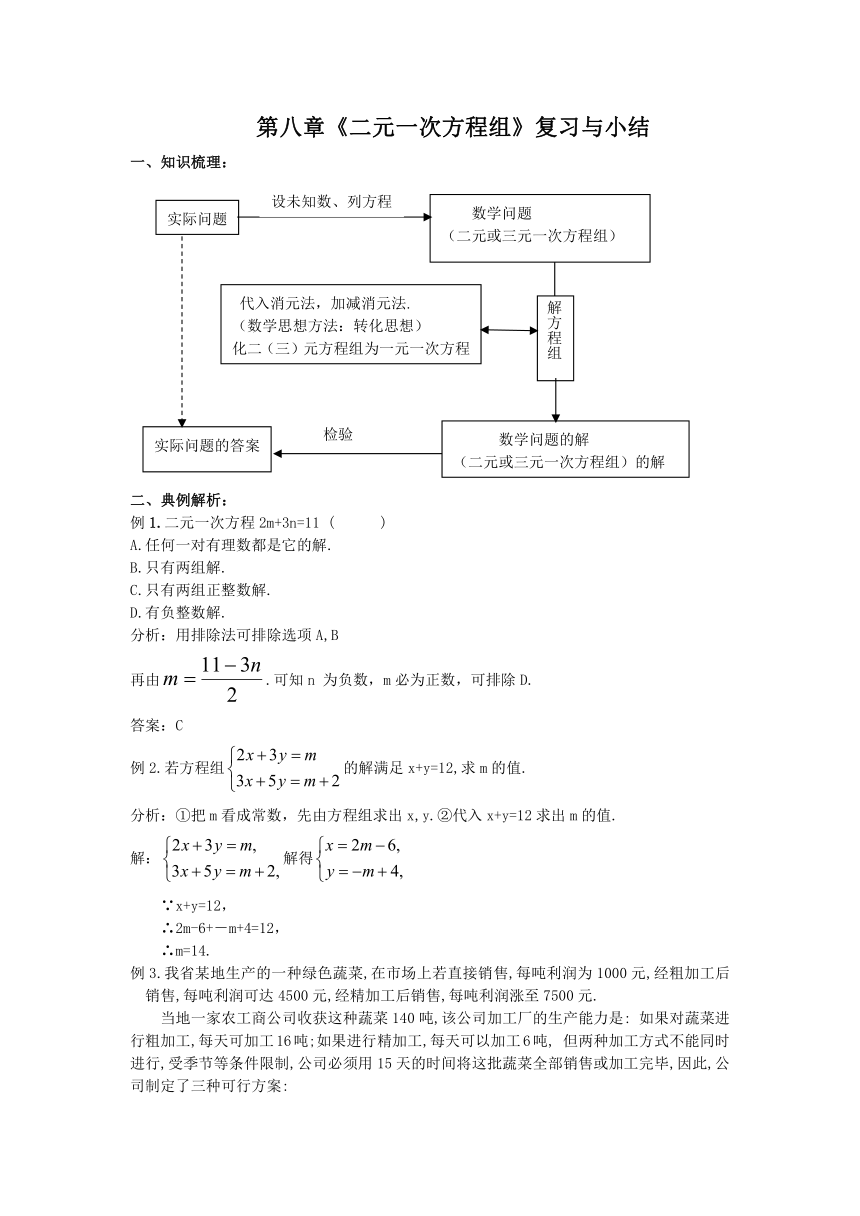
一、知识梳理:
二、典例解析:
例1.二元一次方程2m+3n=11 ( )
A.任何一对有理数都是它的解.
B.只有两组解.
C.只有两组正整数解.
D.有负整数解.
分析:用排除法可排除选项A,B
再由.可知n 为负数,m必为正数,可排除D.
答案:C
例2.若方程组的解满足x+y=12,求m的值.
分析:①把m看成常数,先由方程组求出x,y.②代入x+y=12求出m的值.
解:解得
∵x+y=12,
∴2m-6+-m+4=12,
∴m=14.
例3.我省某地生产的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元.
当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可以加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须用15天的时间将这批蔬菜全部销售或加工完毕,因此,公司制定了三种可行方案:
方案一:将蔬菜全部进行精加工.
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接出售.
方案三:将一部分蔬菜进行精加工,其余蔬菜进行精加工,并恰好用15天完成.
你认为选择哪种方案获利最多 为什么
解:选择第三种方案获利最多.
方案一:因为每天粗加工16吨,140吨可以在15天内加工完,
总利润W1=4500×140=630000(元).
方案二:因为每天精加工6吨,15天可以加工90吨,其余50吨直接销售,
总利润W2=90×7500+50×1000=725000(元).
方案三:设15天内精加工蔬菜x吨,粗加工蔬菜y吨,
依题意得: 解得
总利润W3=60×7500+80×4500=810000(元),
因为W1三、针对练习:毛
1、已知,则x、y的值为( )
A. B. C. D.
2、若与是同类项,则的值等于_______.
3、当=_______时,方程是二元一次方程。
4、是的解,则= 。
5、方程的正整数解为____________________________________。
6、解下列方程组:
⑴、 ⑵、
⑶、 ⑷、
7、已知关于x、y的方程组与同解,求a、b的值.
8、有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨.如果每吨运费30元,求3辆大车与5辆小车所运货物共需要运费多少元?
9、为了拉动内需,广东启动“家电下乡”活动。某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出960台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1228台。
(1)在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为多少台?
(2)若Ⅰ型冰箱每台价格是2298元,Ⅱ型冰箱每台价格是1999元,根据“家电下乡”的有关政策,政府按每台冰箱价格的13%给购买冰箱的农户补贴,问:启动活动后的第一个月销售给农户的1228台Ⅰ型冰箱和Ⅱ型冰箱,政府共补贴了多少元(结果保留2个有效数字)?
10、小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:),解答下列问题:
(1)写出用含x、y的代数式表示的地面总面积;(2)已知客厅面积比卫生间面积多212,且地面总面积是卫生间面积的15倍,铺12地砖的平均费用为80元,求铺地砖的总费用为多少元?
11、某超市为“开业三周年”举行了店庆活动.对、两种商品实行打折出售.打折前,购买5件商品和1件商品需用84元;购买6件商品和3件商品需用108元.而店庆期间,购买50件商品和50件商品仅需960元,这比不打折少花多少钱?
12、某中学拟组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
实际问题
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次方程组)的解
实际问题的答案
代入消元法,加减消元法.
(数学思想方法:转化思想)
化二(三)元方程组为一元一次方程
检验
设未知数、列方程
一、知识梳理:
二、典例解析:
例1.二元一次方程2m+3n=11 ( )
A.任何一对有理数都是它的解.
B.只有两组解.
C.只有两组正整数解.
D.有负整数解.
分析:用排除法可排除选项A,B
再由.可知n 为负数,m必为正数,可排除D.
答案:C
例2.若方程组的解满足x+y=12,求m的值.
分析:①把m看成常数,先由方程组求出x,y.②代入x+y=12求出m的值.
解:解得
∵x+y=12,
∴2m-6+-m+4=12,
∴m=14.
例3.我省某地生产的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元.
当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可以加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须用15天的时间将这批蔬菜全部销售或加工完毕,因此,公司制定了三种可行方案:
方案一:将蔬菜全部进行精加工.
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接出售.
方案三:将一部分蔬菜进行精加工,其余蔬菜进行精加工,并恰好用15天完成.
你认为选择哪种方案获利最多 为什么
解:选择第三种方案获利最多.
方案一:因为每天粗加工16吨,140吨可以在15天内加工完,
总利润W1=4500×140=630000(元).
方案二:因为每天精加工6吨,15天可以加工90吨,其余50吨直接销售,
总利润W2=90×7500+50×1000=725000(元).
方案三:设15天内精加工蔬菜x吨,粗加工蔬菜y吨,
依题意得: 解得
总利润W3=60×7500+80×4500=810000(元),
因为W1
1、已知,则x、y的值为( )
A. B. C. D.
2、若与是同类项,则的值等于_______.
3、当=_______时,方程是二元一次方程。
4、是的解,则= 。
5、方程的正整数解为____________________________________。
6、解下列方程组:
⑴、 ⑵、
⑶、 ⑷、
7、已知关于x、y的方程组与同解,求a、b的值.
8、有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨.如果每吨运费30元,求3辆大车与5辆小车所运货物共需要运费多少元?
9、为了拉动内需,广东启动“家电下乡”活动。某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出960台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1228台。
(1)在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为多少台?
(2)若Ⅰ型冰箱每台价格是2298元,Ⅱ型冰箱每台价格是1999元,根据“家电下乡”的有关政策,政府按每台冰箱价格的13%给购买冰箱的农户补贴,问:启动活动后的第一个月销售给农户的1228台Ⅰ型冰箱和Ⅱ型冰箱,政府共补贴了多少元(结果保留2个有效数字)?
10、小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:),解答下列问题:
(1)写出用含x、y的代数式表示的地面总面积;(2)已知客厅面积比卫生间面积多212,且地面总面积是卫生间面积的15倍,铺12地砖的平均费用为80元,求铺地砖的总费用为多少元?
11、某超市为“开业三周年”举行了店庆活动.对、两种商品实行打折出售.打折前,购买5件商品和1件商品需用84元;购买6件商品和3件商品需用108元.而店庆期间,购买50件商品和50件商品仅需960元,这比不打折少花多少钱?
12、某中学拟组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
实际问题
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次方程组)的解
实际问题的答案
代入消元法,加减消元法.
(数学思想方法:转化思想)
化二(三)元方程组为一元一次方程
检验
设未知数、列方程
