苏科版数学七年级下 11.2三角形全等的判定(HL)
文档属性
| 名称 | 苏科版数学七年级下 11.2三角形全等的判定(HL) |
|
|
| 格式 | zip | ||
| 文件大小 | 223.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览


文档简介
(共30张PPT)
三角形全等的判定(HL)
复习提问
证明一般两个三角形全等有哪些方法
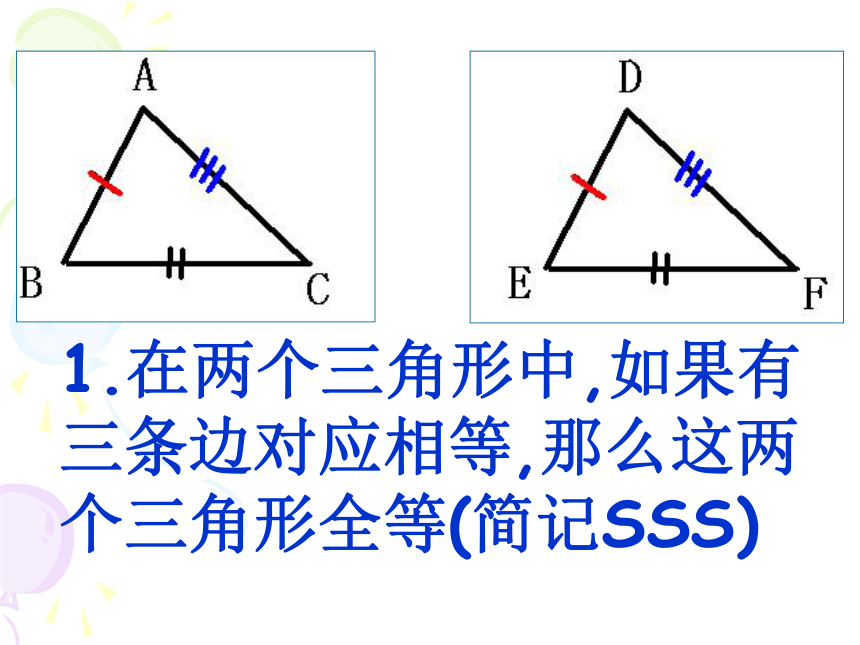
1.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记SSS)
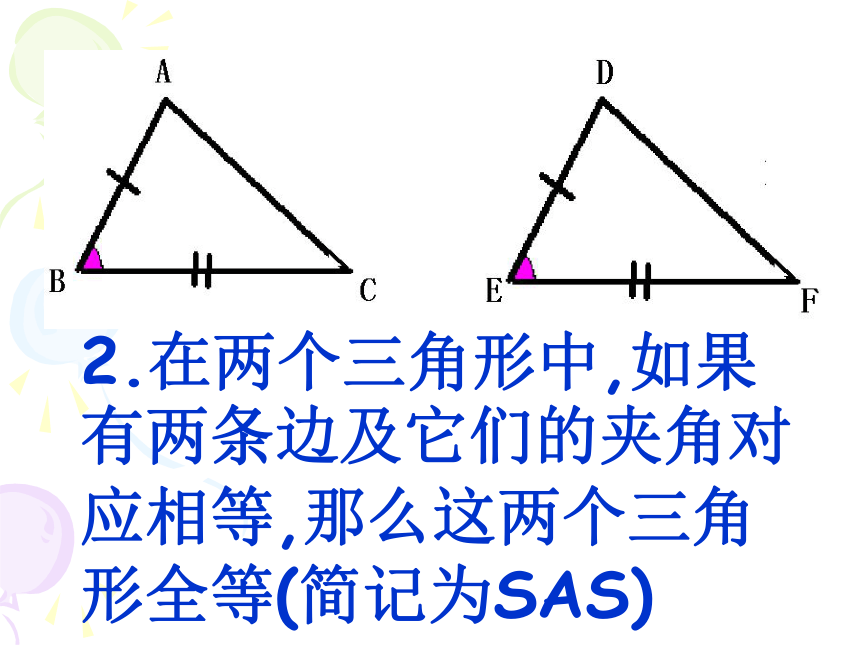
2.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为SAS)
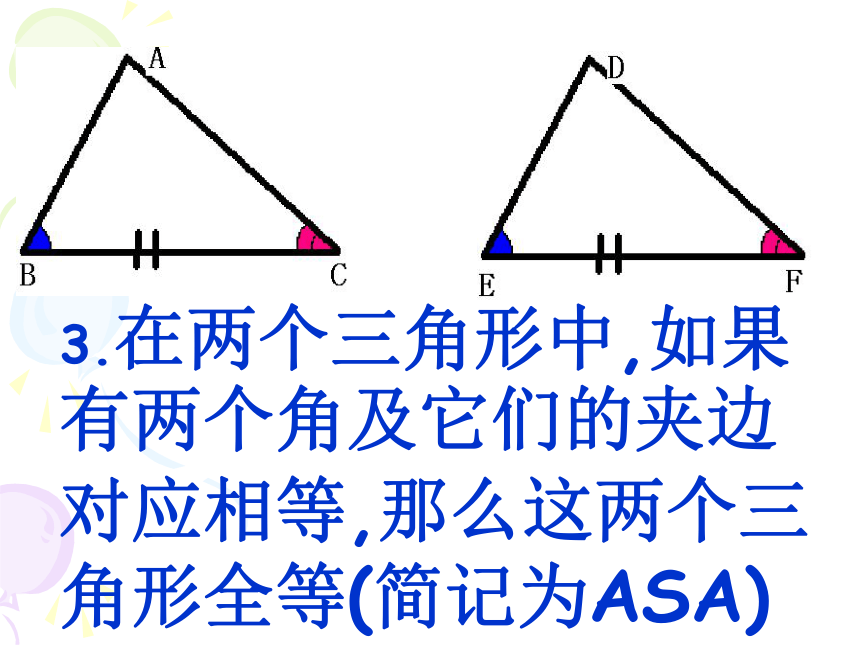
3.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为ASA)
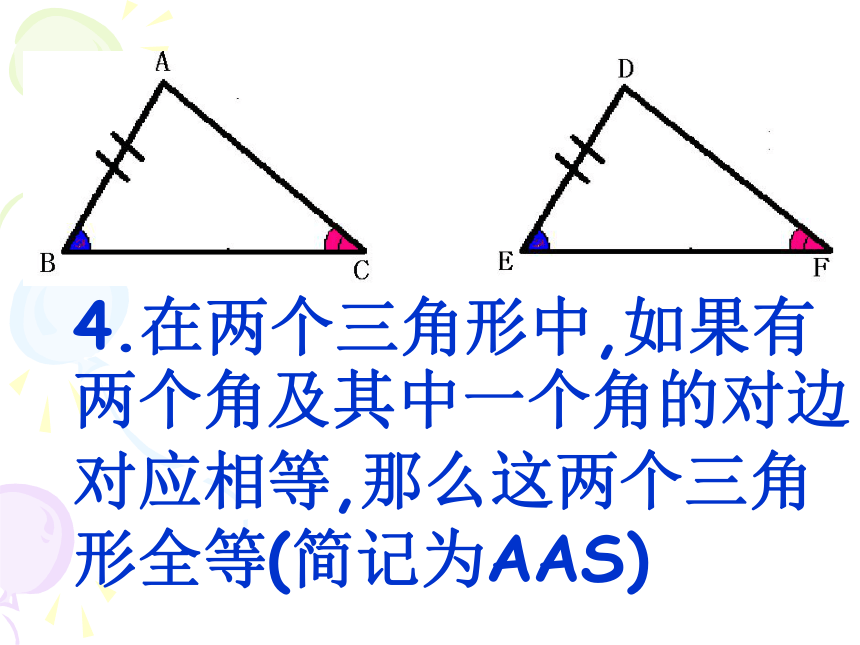
4.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为AAS)
满足下列条件的两个三角形是否全等 为什么
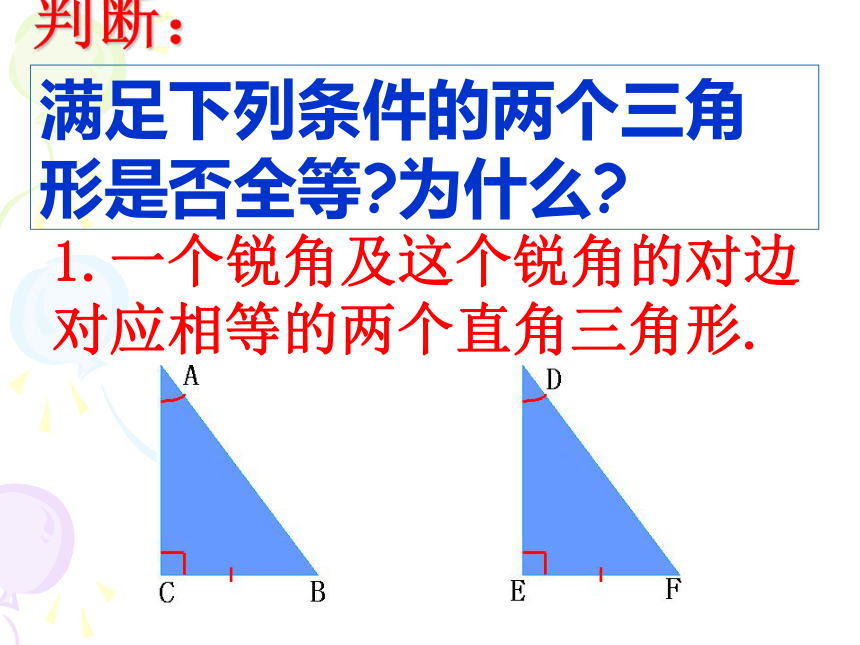
1.一个锐角及这个锐角的对边对应相等的两个直角三角形.
判断:
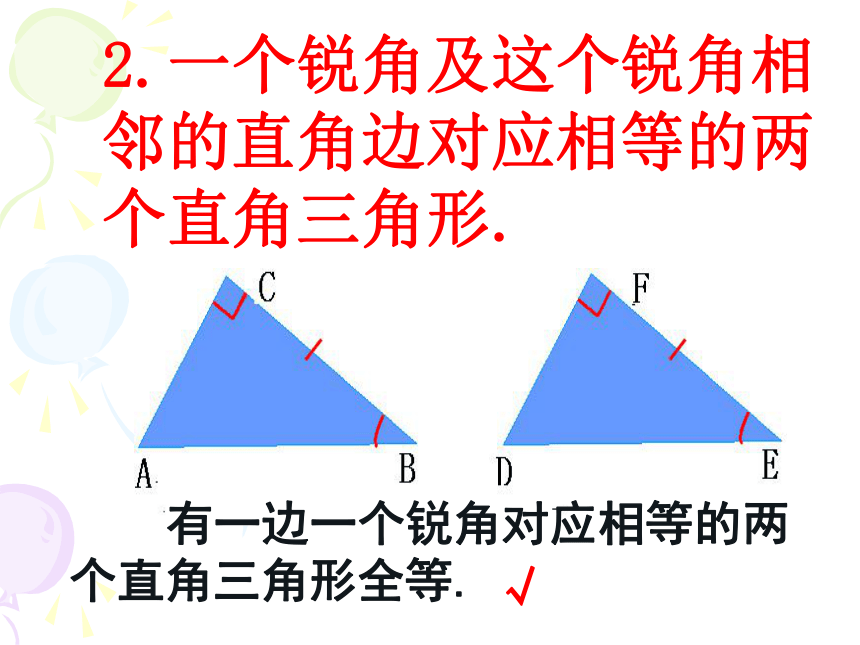
2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
有一边一个锐角对应相等的两个直角三角形全等.
√
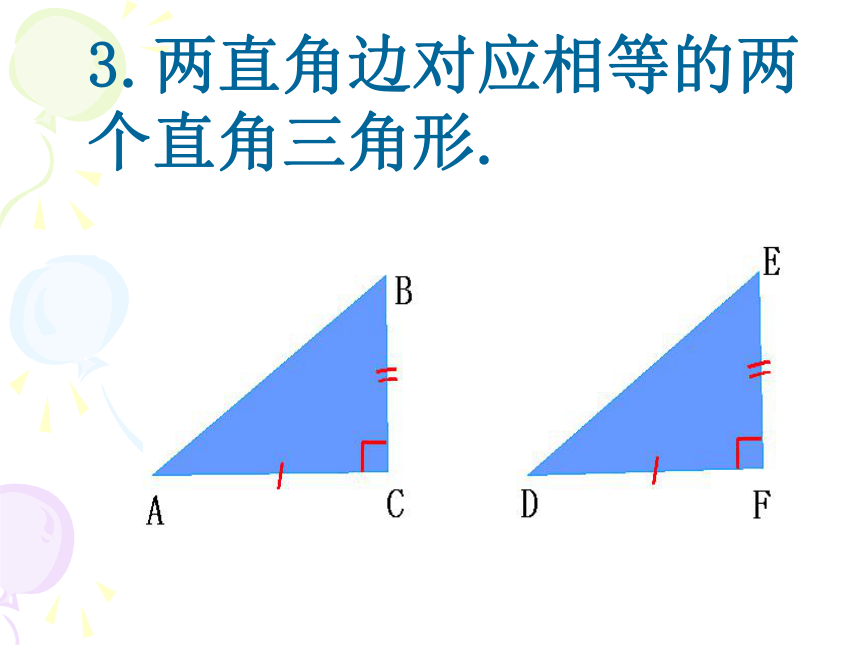
3.两直角边对应相等的两个直角三角形.
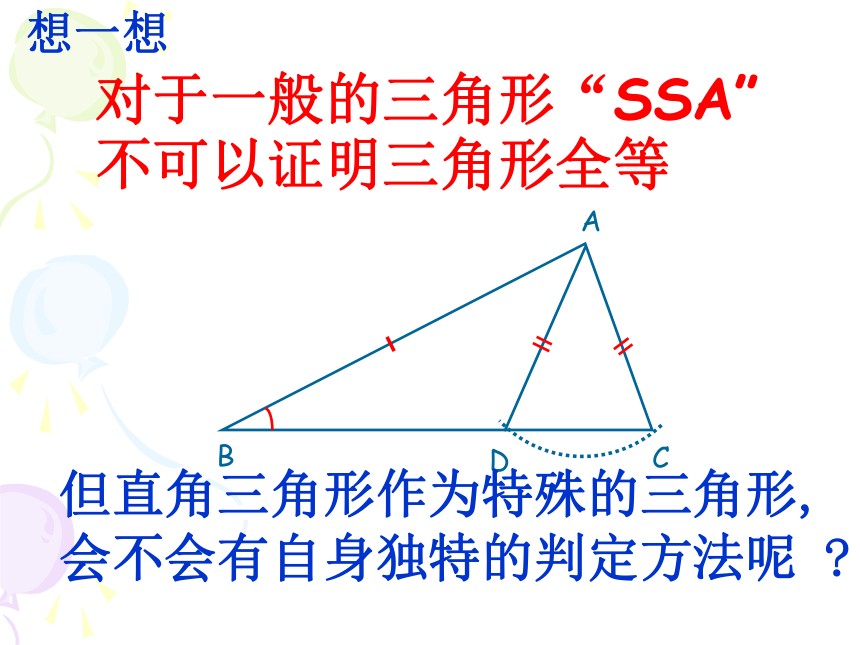
想一想
对于一般的三角形“SSA”不可以证明三角形全等
A
B
C
D
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢
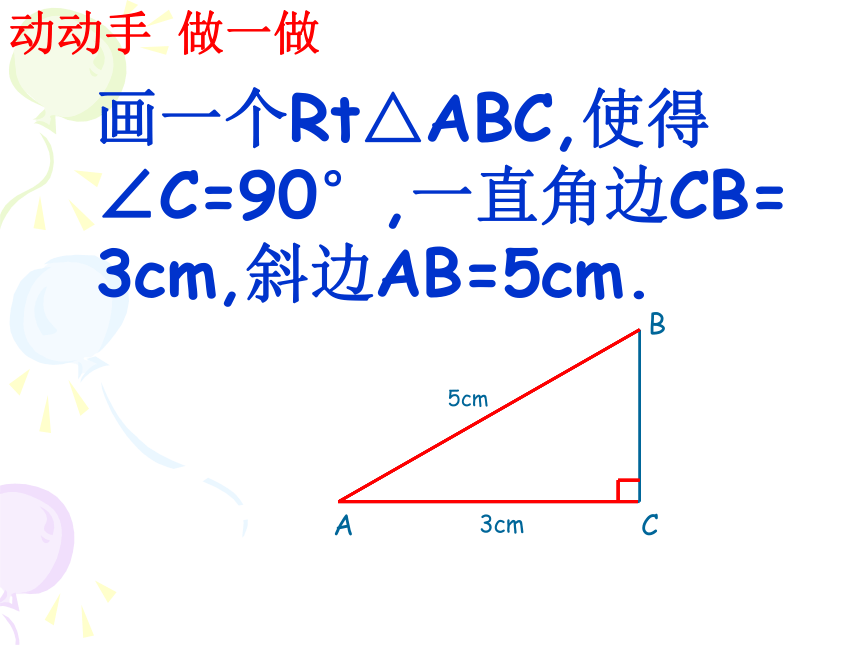
动动手 做一做
画一个Rt△ABC,使得∠C=90°,一直角边CB=
3cm,斜边AB=5cm.
A
B
C
5cm
3cm
动动手 做一做
1:画∠PCQ=90°;
C
Q
P
动动手 做一做
1:画∠PCQ=90°;
C
Q
P
2:在射线CP上截取CB=3cm;
B
1:画∠PCQ=90°;
2:在射线CP上截取CB=3cm;
动动手 做一做
3:以B为圆心,5cm为半径画弧,交射线CQ于A;
C
Q
P
B
A
C
Q
P
A
动动手 做一做
B
4:连结AB;
△ABC即为所要
画的三角形
1:画∠PCQ=90°;
2:在射线CP上截取CB=3cm;
3:以B为圆心,5cm为半径画弧,交射线CQ于A;
把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?
Rt△ABC≌Rt△A′B′C′
B
A
C
5cm
3cm
B’
A’
C’
5cm
3cm
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
斜边、直角边公理 (HL)推理格式
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△
(HL)
例1:如图:AC⊥BC,BD⊥AD,AC=BD.说明:BC=AD.
A
B
C
D
O
在Rt△ACB和Rt△BDA中,则
AB=BA(共公边)
AC=BD.(已知)
∴ Rt△ACB≌Rt△BDA (HL).
∴BC=AD
(全等三角形对应边相等).
解: AC⊥BC,BD⊥AD
∴ ∠D=∠C=90°
例2 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
解:在Rt△ACB和 Rt△ADB中,有
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
3.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE。说明△EBC≌ △DCB的理由。
A
B
C
E
D
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE
巩固练习
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EF
G
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗
C
D
A
F
E
B
G
变式训练2
例3已知:如图,在△ABC和△DEF中,AP、DQ分别是高, 且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
E
F
Q
D
1. 如图∠C= ∠D=Rt ∠ ,要证明△ACB≌ △BDA ,至少再补充几个条件,应补充什么条件?把它们分别写出来。
A
B
C
D
练习
3. 如图,两根长度为12米的绳子,一端系在旗杆上,另一端拉直后分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
解:BD=CD
因为∠ADB=∠ADC=90°
AB=AC
AD=AD
所以Rt△ABD≌Rt△ACD(HL)
所以BD=CD
小结
直角三角形全等的识别
一般三角形全等的识别
S.A.S
A.S.A
A.A.S
S.S.S
S.A.S
A.S.A
A.A.S
H.L
灵活运用各种方法证明直角三角形全等
再见
三角形全等的判定(HL)
复习提问
证明一般两个三角形全等有哪些方法
1.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记SSS)
2.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为SAS)
3.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为ASA)
4.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为AAS)
满足下列条件的两个三角形是否全等 为什么
1.一个锐角及这个锐角的对边对应相等的两个直角三角形.
判断:
2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
有一边一个锐角对应相等的两个直角三角形全等.
√
3.两直角边对应相等的两个直角三角形.
想一想
对于一般的三角形“SSA”不可以证明三角形全等
A
B
C
D
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢
动动手 做一做
画一个Rt△ABC,使得∠C=90°,一直角边CB=
3cm,斜边AB=5cm.
A
B
C
5cm
3cm
动动手 做一做
1:画∠PCQ=90°;
C
Q
P
动动手 做一做
1:画∠PCQ=90°;
C
Q
P
2:在射线CP上截取CB=3cm;
B
1:画∠PCQ=90°;
2:在射线CP上截取CB=3cm;
动动手 做一做
3:以B为圆心,5cm为半径画弧,交射线CQ于A;
C
Q
P
B
A
C
Q
P
A
动动手 做一做
B
4:连结AB;
△ABC即为所要
画的三角形
1:画∠PCQ=90°;
2:在射线CP上截取CB=3cm;
3:以B为圆心,5cm为半径画弧,交射线CQ于A;
把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?
Rt△ABC≌Rt△A′B′C′
B
A
C
5cm
3cm
B’
A’
C’
5cm
3cm
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
斜边、直角边公理 (HL)推理格式
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△
(HL)
例1:如图:AC⊥BC,BD⊥AD,AC=BD.说明:BC=AD.
A
B
C
D
O
在Rt△ACB和Rt△BDA中,则
AB=BA(共公边)
AC=BD.(已知)
∴ Rt△ACB≌Rt△BDA (HL).
∴BC=AD
(全等三角形对应边相等).
解: AC⊥BC,BD⊥AD
∴ ∠D=∠C=90°
例2 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
解:在Rt△ACB和 Rt△ADB中,有
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
3.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE。说明△EBC≌ △DCB的理由。
A
B
C
E
D
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE
巩固练习
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EF
G
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗
C
D
A
F
E
B
G
变式训练2
例3已知:如图,在△ABC和△DEF中,AP、DQ分别是高, 且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
E
F
Q
D
1. 如图∠C= ∠D=Rt ∠ ,要证明△ACB≌ △BDA ,至少再补充几个条件,应补充什么条件?把它们分别写出来。
A
B
C
D
练习
3. 如图,两根长度为12米的绳子,一端系在旗杆上,另一端拉直后分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
解:BD=CD
因为∠ADB=∠ADC=90°
AB=AC
AD=AD
所以Rt△ABD≌Rt△ACD(HL)
所以BD=CD
小结
直角三角形全等的识别
一般三角形全等的识别
S.A.S
A.S.A
A.A.S
S.S.S
S.A.S
A.S.A
A.A.S
H.L
灵活运用各种方法证明直角三角形全等
再见
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
