湖南省岳阳市2020-2021学年八年级下学期期末数学试卷(word版含解析)
文档属性
| 名称 | 湖南省岳阳市2020-2021学年八年级下学期期末数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 263.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
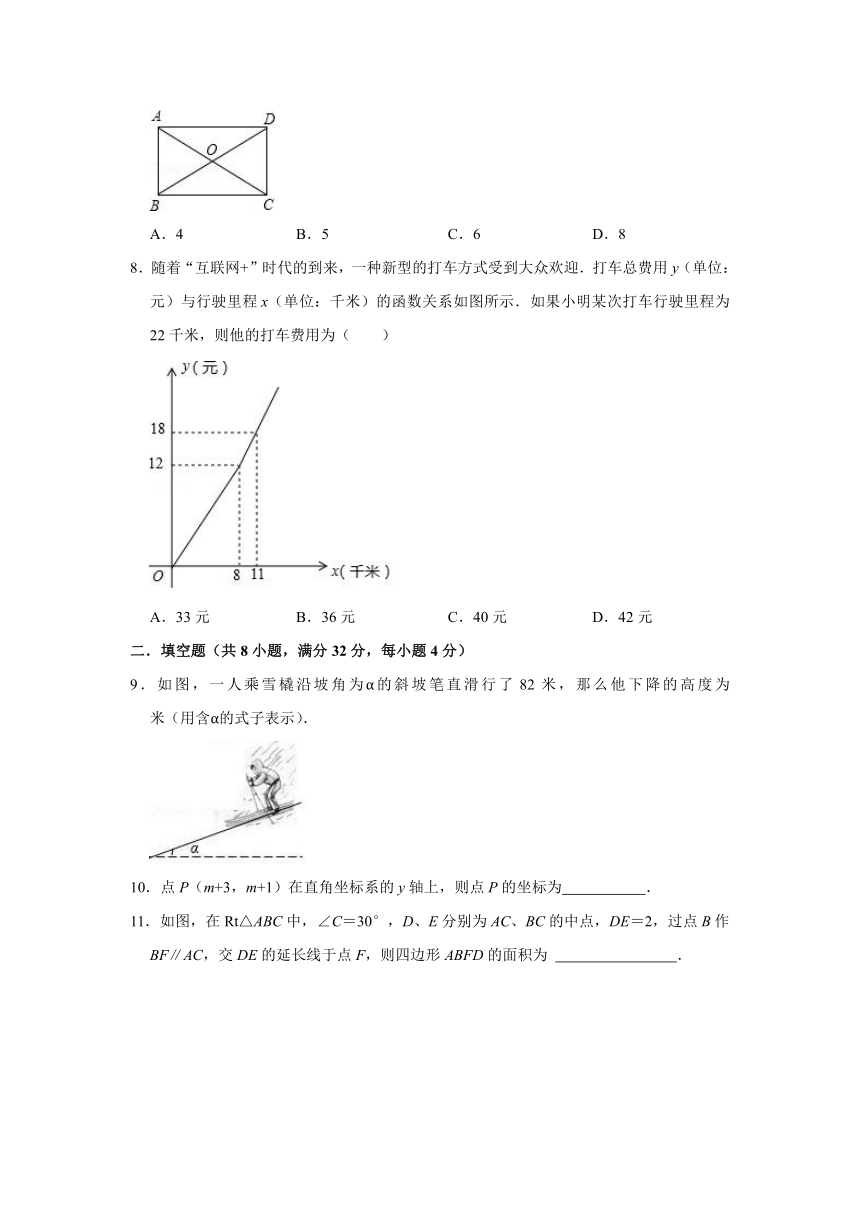
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 06:02:31 | ||
图片预览


文档简介
2020-2021学年八年级(下)期末数学试卷
一.选择题(共8小题,满分24分,每小题3分)
1.若一个正多边形的每一个外角都等于40°,则这个正多边形的边数是( )
A.7 B.8 C.9 D.10
2.平面直角坐标系中,点M(m﹣2,m+3)在x轴上,则m的值为( )
A.﹣3 B.﹣2 C.2 D.3
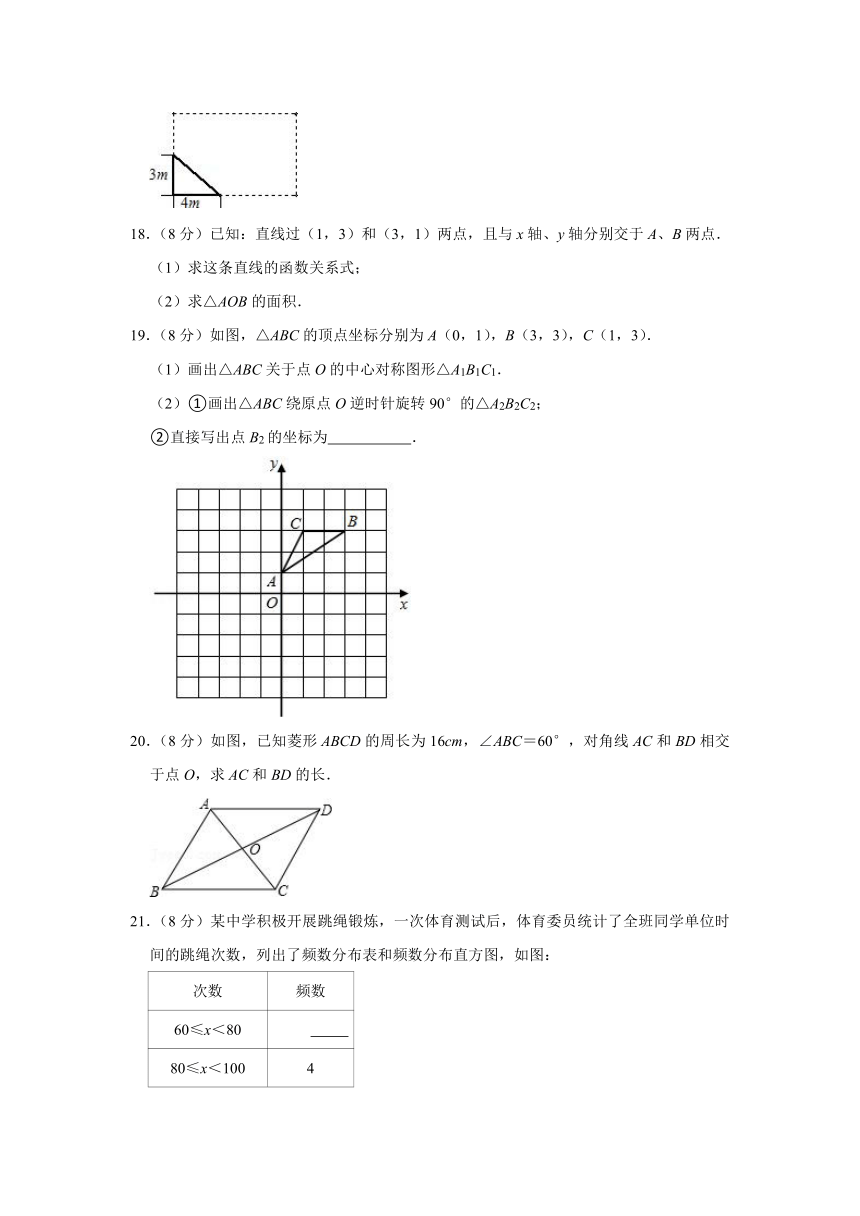
3.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.1,1, C.6,8,11 D.5,12,23
4.一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
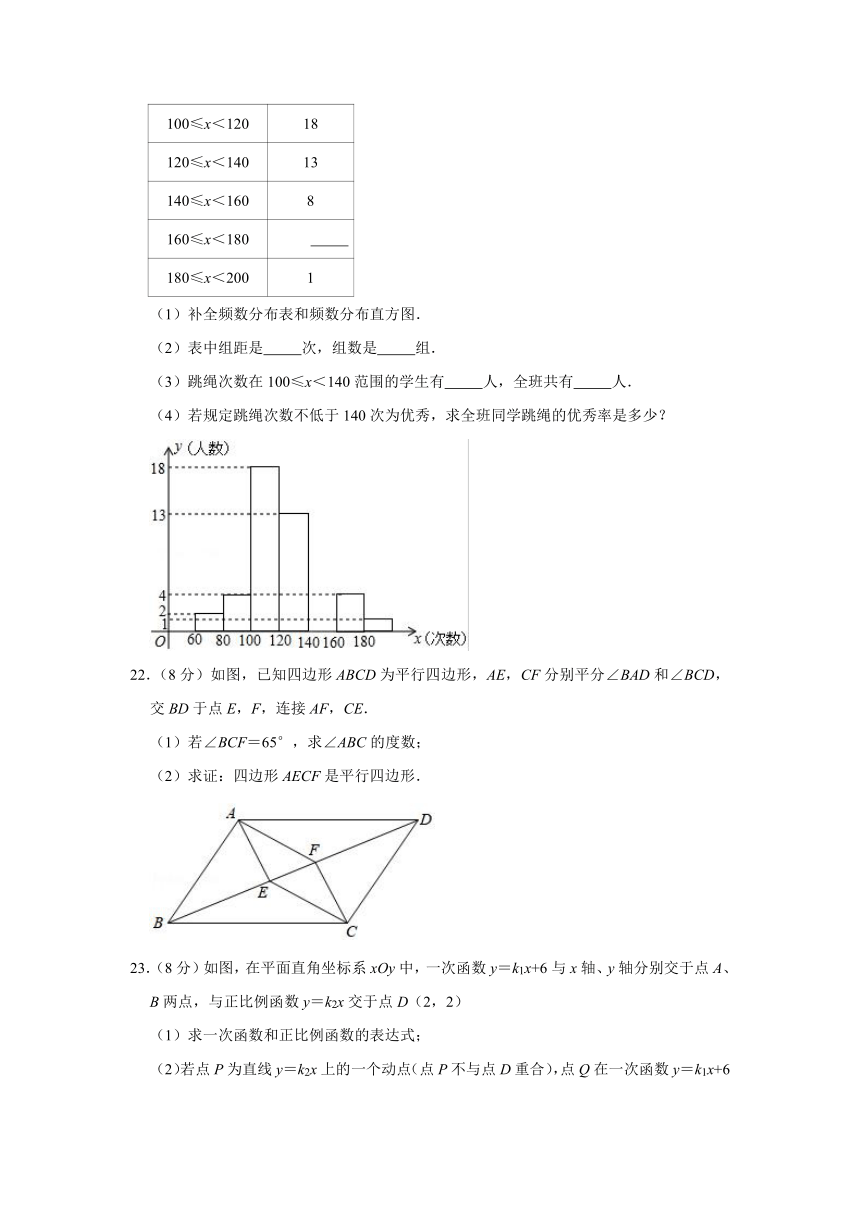
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
5.如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,以下判断中正确的个数有( )
①∠DCB=∠A;②∠DCB=∠ACE;③∠ACD=∠BCE;④∠BCE=∠BEC.
A.1个 B.2个 C.3个 D.4个
6.有40个数据,共分成6组,第1﹣4组的频数分别是10,5,7,6,第5组的频率为0.10,则第6组的频率为( )
A.0.25 B.0.30 C.0.15 D.0.20
7.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
8.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元 B.36元 C.40元 D.42元
二.填空题(共8小题,满分32分,每小题4分)
9.如图,一人乘雪橇沿坡角为α的斜坡笔直滑行了82米,那么他下降的高度为 米(用含α的式子表示).
10.点P(m+3,m+1)在直角坐标系的y轴上,则点P的坐标为 .
11.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
12.一组数据共50个,分为6组,第1﹣4组的频数分别是5,7,8,10,第5组的频率是0.20,那么第6组的频数是 .
13.AD是△ABC中∠BAC的平分线,DE⊥AB于点E,若S△ABC=10,DE=2,AB=4,则AC的长是 .
14.在?ABCD中,对角线AC,BD相交于点O,请你补充一个条件 ,使?ABCD是矩形.
15.已知一次函数y=kx+1(k为常数,k≠0),y随x的增大而减小,则k的值可以是 (写出一个即可).
16.平面直角坐标系中,四边形OABC是矩形,点A(10,0),点C(0,3),点D是OA的中点,点P是BC边上的一个动点,当△POD是腰长为5的等腰三角形时,点P的坐标为 .
A.(1,3)
B.(,3)
C.(4,3)
D.(9,3)
三.解答题(共8小题,满分64分,每小题8分)
17.(8分)如图,学校有一块长方形花坛,有极少数人为了避开拐角走“捷径”,在花坛内走出了一条“路”,他们仅仅少走了 m,却踩伤了花草.
18.(8分)已知:直线过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点.
(1)求这条直线的函数关系式;
(2)求△AOB的面积.
19.(8分)如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1.
(2)①画出△ABC绕原点O逆时针旋转90°的△A2B2C2;
②直接写出点B2的坐标为 .
20.(8分)如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
21.(8分)某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和频数分布直方图,如图:
次数 频数
60≤x<80
80≤x<100 4
100≤x<120 18
120≤x<140 13
140≤x<160 8
160≤x<180
180≤x<200 1
(1)补全频数分布表和频数分布直方图.
(2)表中组距是 次,组数是 组.
(3)跳绳次数在100≤x<140范围的学生有 人,全班共有 人.
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
22.(8分)如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE.
(1)若∠BCF=65°,求∠ABC的度数;
(2)求证:四边形AECF是平行四边形.
23.(8分)如图,在平面直角坐标系xOy中,一次函数y=k1x+6与x轴、y轴分别交于点A、B两点,与正比例函数y=k2x交于点D(2,2)
(1)求一次函数和正比例函数的表达式;
(2)若点P为直线y=k2x上的一个动点(点P不与点D重合),点Q在一次函数y=k1x+6的图象上,PQ∥y轴,当PQ=OA时,求点p的坐标.
24.(8分)已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
(1)当m=6时,求点B的坐标;
(2)当m=﹣6时,求点B的坐标;
(3)若点Q(﹣1,0),当BQ最小时,直接写出m的值.
参考答案
一.选择题(共8小题,满分24分,每小题3分)
1.解:∵360÷40=9,
∴这个多边形的边数是9.
故选:C.
2.解:∵点M(m﹣2,m+3)在x轴上,
∴m+3=0,
解得m=﹣3,
故选:A.
3.解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;
B、∵12+12=,∴能构成直角三角形,故B正确;
C、∵62+82≠112,∴不能构成直角三角形,故C错误;
D、∵52+122≠232,∴不能构成直角三角形,故D错误.
故选:B.
4.解:∵一个正多边形绕着它的中心旋转45°后,能与原正多边形重合,
360°÷45°=8,
∴这个正多边形是正八边形.
正八边形既是轴对称图形,又是中心对称图形.
故选:C.
5.解:∵CD⊥AB,
∴∠CDB=90°,
∵∠ACB=90°,
∴∠A+∠B=∠BCD+∠B=90°,
∴∠DCB=∠A,故①正确;
∵CE是斜边AB上的中线,
∴AE=CE=BE,
∴∠A=∠ACE,
∴∠DCB=∠ACE,故②正确;
∵∠A+∠ACD=90°,
∴∠ACD=∠B,
∵CE=BE,
∴∠BCE=∠B,
∴∠ACD=∠BCE,故③正确;
∵BC不一定等于BE,
∴∠BCE不一定等于∠BEC,故④错误;
故选:C.
6.解:∵第5组的频率为0.10,
∴第5组的频数为40×0.1=4,
∴第6组的频数为40﹣(10+5+7+6+4)=8,
故第6组的频率为=0.2.
故选:D.
7.解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=4,
故选:A.
8.解:当行驶里程x≥8时,设y=kx+b,
将(8,12)、(11,18)代入,
得:,
解得:,
∴y=2x﹣4,
当x=22时,y=2×22﹣4=40,
∴如果小明某次打车行驶里程为22千米,则他的打车费用为40元;
故选:C.
二.填空题(共8小题,满分32分,每小题4分)
9.解:如图,设下滑的距离为AB=82米,下降的高度为线段AC.
在Rt△ABC中,AC=AB?sinα=82?sinα,
故答案为82?sinα.
10.解:∵点P(m+3,m+1)在直角坐标系的y轴上,
∴m+3=0,
解得:m=﹣3,
故m+1=﹣2,
则点P的坐标为:(0,﹣2).
故答案为:(0,﹣2).
11.解:∵D、E分别为AC、BC的中点,
即DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴AB=2DE,DF∥AB,
又∵BF∥AC,
∴BF∥AD,
∴四边形ABFD是平行四边形,
∵AB⊥BE,
∴S平行四边形ABFD=AB?BE,
∵DE=2,
∴AB=2×2=4,
在Rt△ABC中,
∵∠C=30°,
∴AC=2AB=2×4=8,
∴BC===4,
∴BE=BC=2,
∴S平行四边形ABFD=4×2=8,
故答案为8.
12.解:第5组的频数:50×0.2=10,
第6组的频数是:50﹣5﹣7﹣8﹣10﹣10=10,
故答案为:10.
13.解:作DF⊥AC交AC于点F,
∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴10=×4×2+×AC×2,
∴AC=6.
故答案为:6
14.解:若使?ABCD变为矩形,可添加的条件是:
AC=BD;(对角线相等的平行四边形是矩形)
∠ABC=90°等.(有一个角是直角的平行四边形是矩形)
故答案为:AC=BD
15.解:∵一次函数y随x的增大而减小,
∴k<0,
不妨设k=﹣1,
故答案为:﹣1
16.解:过P作PM⊥OA于M.
(1)当OP=OD=5时,
∵OP=5,CO=3,
∴CP===4,
∴P(4,3);
(2)当OD=PD=5时,
∵PD=DO=5,PM=3,
∴MD===4,
∴CP=1或CP′=9,
∴P(1,3)或(9,3);
综上,满足题意的点P的坐标为(4,3)、(1,3)、(9,3).
故答案为:A、C、D.
三.解答题(共8小题,满分64分,每小题8分)
17.解:由题意得,斜边长为:=5m,
故少走的路程=两直角边之和﹣斜边=3+4﹣5=2m.
故答案为:2.
18.解:(1)设直线的函数关系式为y=kx+b(k≠0),
把(1,3),(3,1)代入得,
解方程组得,
∴这条直线的函数关系式为y=﹣x+4;
(2)当x=0时,y=4,
∴B(0,4),
当y=0,则﹣x+4=0,
解得x=4,
∴A(4,0),
∴S△AOB=AO?BO=×4×4=8.
19.解:(1)如图,△A1B1C1为所作;
(2)①画如图,△A2B2C2为所作;
②点B2的坐标为(﹣3,3).
故答案为(﹣3,3).
20.解:∵菱形ABCD的周长为16cm,∠ABC=60°
∴AB=BC=4cm,△ABC是等边三角形,
∴AC=4cm
∵AC、BD互相垂直平分
∴OA=2
∴OB==2cm
∴BD=4cm
21.解:(1)如图,成绩在60≤x<80的人数为2人,成绩在160≤x<180的人数为4人,
(2)表中组距是20次,组数是7组.
(3)跳绳次数在100≤x<140范围的学生有31人,全班人数为2+4+18+13+8+4+1=50(人);
故答案为2,4;20,7;31,50;
(4)跳绳次数不低于140次的人数为8+4+1=13,
所以全班同学跳绳的优秀率=×100%=26%.
22.(1)解:∵CF平分∠BCD,
∴∠BCD=2∠BCF=65°×2=130°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC=180°﹣∠BCD=180°﹣130°=50°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(ASA).
∴∠AEB=∠CFD,AE=CF,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形.
23.解:(1)把(2,2)分别代入y=k1x+6与y=k2x得,
k1=﹣2,k2=1,
∴一次函数和正比例函数的表达式分别为:y=﹣2x+6,y=x;
(2)由y=﹣2x+6,当y=0时,得x=3,
∴A(3,0),
∴OA=3,
∵点P(m,n),
∴Q(m,﹣2m+6),
当PQ=OA时,PQ=m﹣(﹣2m+6)=×3,或PQ=﹣2m+6﹣m=×3,
解得:m=或m=,
∴P(,),(,).
24.解:(1)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,6),
∴BD=CO=4,CD=AO=6,
∴OD=10,
∴此时,点B的坐标为(10,4);
(2)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,﹣6),
∴BD=CO=4,CD=AO=6,
∴OD=2,
∴此时,点B的坐标为(﹣2,4);
(3)如图所示,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),
∴BD=CO=4,
连接BQ,则当点D与点Q重合时,BD=BQ=4,
根据垂线段最短,可知此时BQ最小,
∵Q(﹣1,0),C(4,0),
∴此时,AO=CQ=5,
又∵点A在y轴负半轴上,
∴m的值为﹣5.
一.选择题(共8小题,满分24分,每小题3分)
1.若一个正多边形的每一个外角都等于40°,则这个正多边形的边数是( )
A.7 B.8 C.9 D.10
2.平面直角坐标系中,点M(m﹣2,m+3)在x轴上,则m的值为( )
A.﹣3 B.﹣2 C.2 D.3
3.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.1,1, C.6,8,11 D.5,12,23
4.一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
5.如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,以下判断中正确的个数有( )
①∠DCB=∠A;②∠DCB=∠ACE;③∠ACD=∠BCE;④∠BCE=∠BEC.
A.1个 B.2个 C.3个 D.4个
6.有40个数据,共分成6组,第1﹣4组的频数分别是10,5,7,6,第5组的频率为0.10,则第6组的频率为( )
A.0.25 B.0.30 C.0.15 D.0.20
7.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
8.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元 B.36元 C.40元 D.42元
二.填空题(共8小题,满分32分,每小题4分)
9.如图,一人乘雪橇沿坡角为α的斜坡笔直滑行了82米,那么他下降的高度为 米(用含α的式子表示).
10.点P(m+3,m+1)在直角坐标系的y轴上,则点P的坐标为 .
11.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
12.一组数据共50个,分为6组,第1﹣4组的频数分别是5,7,8,10,第5组的频率是0.20,那么第6组的频数是 .
13.AD是△ABC中∠BAC的平分线,DE⊥AB于点E,若S△ABC=10,DE=2,AB=4,则AC的长是 .
14.在?ABCD中,对角线AC,BD相交于点O,请你补充一个条件 ,使?ABCD是矩形.
15.已知一次函数y=kx+1(k为常数,k≠0),y随x的增大而减小,则k的值可以是 (写出一个即可).
16.平面直角坐标系中,四边形OABC是矩形,点A(10,0),点C(0,3),点D是OA的中点,点P是BC边上的一个动点,当△POD是腰长为5的等腰三角形时,点P的坐标为 .
A.(1,3)
B.(,3)
C.(4,3)
D.(9,3)
三.解答题(共8小题,满分64分,每小题8分)
17.(8分)如图,学校有一块长方形花坛,有极少数人为了避开拐角走“捷径”,在花坛内走出了一条“路”,他们仅仅少走了 m,却踩伤了花草.
18.(8分)已知:直线过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点.
(1)求这条直线的函数关系式;
(2)求△AOB的面积.
19.(8分)如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1.
(2)①画出△ABC绕原点O逆时针旋转90°的△A2B2C2;
②直接写出点B2的坐标为 .
20.(8分)如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
21.(8分)某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和频数分布直方图,如图:
次数 频数
60≤x<80
80≤x<100 4
100≤x<120 18
120≤x<140 13
140≤x<160 8
160≤x<180
180≤x<200 1
(1)补全频数分布表和频数分布直方图.
(2)表中组距是 次,组数是 组.
(3)跳绳次数在100≤x<140范围的学生有 人,全班共有 人.
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
22.(8分)如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE.
(1)若∠BCF=65°,求∠ABC的度数;
(2)求证:四边形AECF是平行四边形.
23.(8分)如图,在平面直角坐标系xOy中,一次函数y=k1x+6与x轴、y轴分别交于点A、B两点,与正比例函数y=k2x交于点D(2,2)
(1)求一次函数和正比例函数的表达式;
(2)若点P为直线y=k2x上的一个动点(点P不与点D重合),点Q在一次函数y=k1x+6的图象上,PQ∥y轴,当PQ=OA时,求点p的坐标.
24.(8分)已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
(1)当m=6时,求点B的坐标;
(2)当m=﹣6时,求点B的坐标;
(3)若点Q(﹣1,0),当BQ最小时,直接写出m的值.
参考答案
一.选择题(共8小题,满分24分,每小题3分)
1.解:∵360÷40=9,
∴这个多边形的边数是9.
故选:C.
2.解:∵点M(m﹣2,m+3)在x轴上,
∴m+3=0,
解得m=﹣3,
故选:A.
3.解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;
B、∵12+12=,∴能构成直角三角形,故B正确;
C、∵62+82≠112,∴不能构成直角三角形,故C错误;
D、∵52+122≠232,∴不能构成直角三角形,故D错误.
故选:B.
4.解:∵一个正多边形绕着它的中心旋转45°后,能与原正多边形重合,
360°÷45°=8,
∴这个正多边形是正八边形.
正八边形既是轴对称图形,又是中心对称图形.
故选:C.
5.解:∵CD⊥AB,
∴∠CDB=90°,
∵∠ACB=90°,
∴∠A+∠B=∠BCD+∠B=90°,
∴∠DCB=∠A,故①正确;
∵CE是斜边AB上的中线,
∴AE=CE=BE,
∴∠A=∠ACE,
∴∠DCB=∠ACE,故②正确;
∵∠A+∠ACD=90°,
∴∠ACD=∠B,
∵CE=BE,
∴∠BCE=∠B,
∴∠ACD=∠BCE,故③正确;
∵BC不一定等于BE,
∴∠BCE不一定等于∠BEC,故④错误;
故选:C.
6.解:∵第5组的频率为0.10,
∴第5组的频数为40×0.1=4,
∴第6组的频数为40﹣(10+5+7+6+4)=8,
故第6组的频率为=0.2.
故选:D.
7.解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=4,
故选:A.
8.解:当行驶里程x≥8时,设y=kx+b,
将(8,12)、(11,18)代入,
得:,
解得:,
∴y=2x﹣4,
当x=22时,y=2×22﹣4=40,
∴如果小明某次打车行驶里程为22千米,则他的打车费用为40元;
故选:C.
二.填空题(共8小题,满分32分,每小题4分)
9.解:如图,设下滑的距离为AB=82米,下降的高度为线段AC.
在Rt△ABC中,AC=AB?sinα=82?sinα,
故答案为82?sinα.
10.解:∵点P(m+3,m+1)在直角坐标系的y轴上,
∴m+3=0,
解得:m=﹣3,
故m+1=﹣2,
则点P的坐标为:(0,﹣2).
故答案为:(0,﹣2).
11.解:∵D、E分别为AC、BC的中点,
即DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴AB=2DE,DF∥AB,
又∵BF∥AC,
∴BF∥AD,
∴四边形ABFD是平行四边形,
∵AB⊥BE,
∴S平行四边形ABFD=AB?BE,
∵DE=2,
∴AB=2×2=4,
在Rt△ABC中,
∵∠C=30°,
∴AC=2AB=2×4=8,
∴BC===4,
∴BE=BC=2,
∴S平行四边形ABFD=4×2=8,
故答案为8.
12.解:第5组的频数:50×0.2=10,
第6组的频数是:50﹣5﹣7﹣8﹣10﹣10=10,
故答案为:10.
13.解:作DF⊥AC交AC于点F,
∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴10=×4×2+×AC×2,
∴AC=6.
故答案为:6
14.解:若使?ABCD变为矩形,可添加的条件是:
AC=BD;(对角线相等的平行四边形是矩形)
∠ABC=90°等.(有一个角是直角的平行四边形是矩形)
故答案为:AC=BD
15.解:∵一次函数y随x的增大而减小,
∴k<0,
不妨设k=﹣1,
故答案为:﹣1
16.解:过P作PM⊥OA于M.
(1)当OP=OD=5时,
∵OP=5,CO=3,
∴CP===4,
∴P(4,3);
(2)当OD=PD=5时,
∵PD=DO=5,PM=3,
∴MD===4,
∴CP=1或CP′=9,
∴P(1,3)或(9,3);
综上,满足题意的点P的坐标为(4,3)、(1,3)、(9,3).
故答案为:A、C、D.
三.解答题(共8小题,满分64分,每小题8分)
17.解:由题意得,斜边长为:=5m,
故少走的路程=两直角边之和﹣斜边=3+4﹣5=2m.
故答案为:2.
18.解:(1)设直线的函数关系式为y=kx+b(k≠0),
把(1,3),(3,1)代入得,
解方程组得,
∴这条直线的函数关系式为y=﹣x+4;
(2)当x=0时,y=4,
∴B(0,4),
当y=0,则﹣x+4=0,
解得x=4,
∴A(4,0),
∴S△AOB=AO?BO=×4×4=8.
19.解:(1)如图,△A1B1C1为所作;
(2)①画如图,△A2B2C2为所作;
②点B2的坐标为(﹣3,3).
故答案为(﹣3,3).
20.解:∵菱形ABCD的周长为16cm,∠ABC=60°
∴AB=BC=4cm,△ABC是等边三角形,
∴AC=4cm
∵AC、BD互相垂直平分
∴OA=2
∴OB==2cm
∴BD=4cm
21.解:(1)如图,成绩在60≤x<80的人数为2人,成绩在160≤x<180的人数为4人,
(2)表中组距是20次,组数是7组.
(3)跳绳次数在100≤x<140范围的学生有31人,全班人数为2+4+18+13+8+4+1=50(人);
故答案为2,4;20,7;31,50;
(4)跳绳次数不低于140次的人数为8+4+1=13,
所以全班同学跳绳的优秀率=×100%=26%.
22.(1)解:∵CF平分∠BCD,
∴∠BCD=2∠BCF=65°×2=130°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC=180°﹣∠BCD=180°﹣130°=50°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(ASA).
∴∠AEB=∠CFD,AE=CF,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形.
23.解:(1)把(2,2)分别代入y=k1x+6与y=k2x得,
k1=﹣2,k2=1,
∴一次函数和正比例函数的表达式分别为:y=﹣2x+6,y=x;
(2)由y=﹣2x+6,当y=0时,得x=3,
∴A(3,0),
∴OA=3,
∵点P(m,n),
∴Q(m,﹣2m+6),
当PQ=OA时,PQ=m﹣(﹣2m+6)=×3,或PQ=﹣2m+6﹣m=×3,
解得:m=或m=,
∴P(,),(,).
24.解:(1)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,6),
∴BD=CO=4,CD=AO=6,
∴OD=10,
∴此时,点B的坐标为(10,4);
(2)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,﹣6),
∴BD=CO=4,CD=AO=6,
∴OD=2,
∴此时,点B的坐标为(﹣2,4);
(3)如图所示,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),
∴BD=CO=4,
连接BQ,则当点D与点Q重合时,BD=BQ=4,
根据垂线段最短,可知此时BQ最小,
∵Q(﹣1,0),C(4,0),
∴此时,AO=CQ=5,
又∵点A在y轴负半轴上,
∴m的值为﹣5.
同课章节目录
