二元一次方程组回顾与复习

课题 二元一次方程组回顾与复习 课型 复习课
教学目标 1、准确理解二元一次方程（组）理解的概念，并熟练地运用代入消元法、加减消元法、图像法解二元一次方程组。2、用二元一次方程组解决问题，熟练建模；3、进一步掌握二元一次方程与一次函数的联系。
重点 解二元一次方程组，用二元一次方程组解决问题
难点 二元一次方程与一次函数的联系
教学环节 教学内容 措施矫正
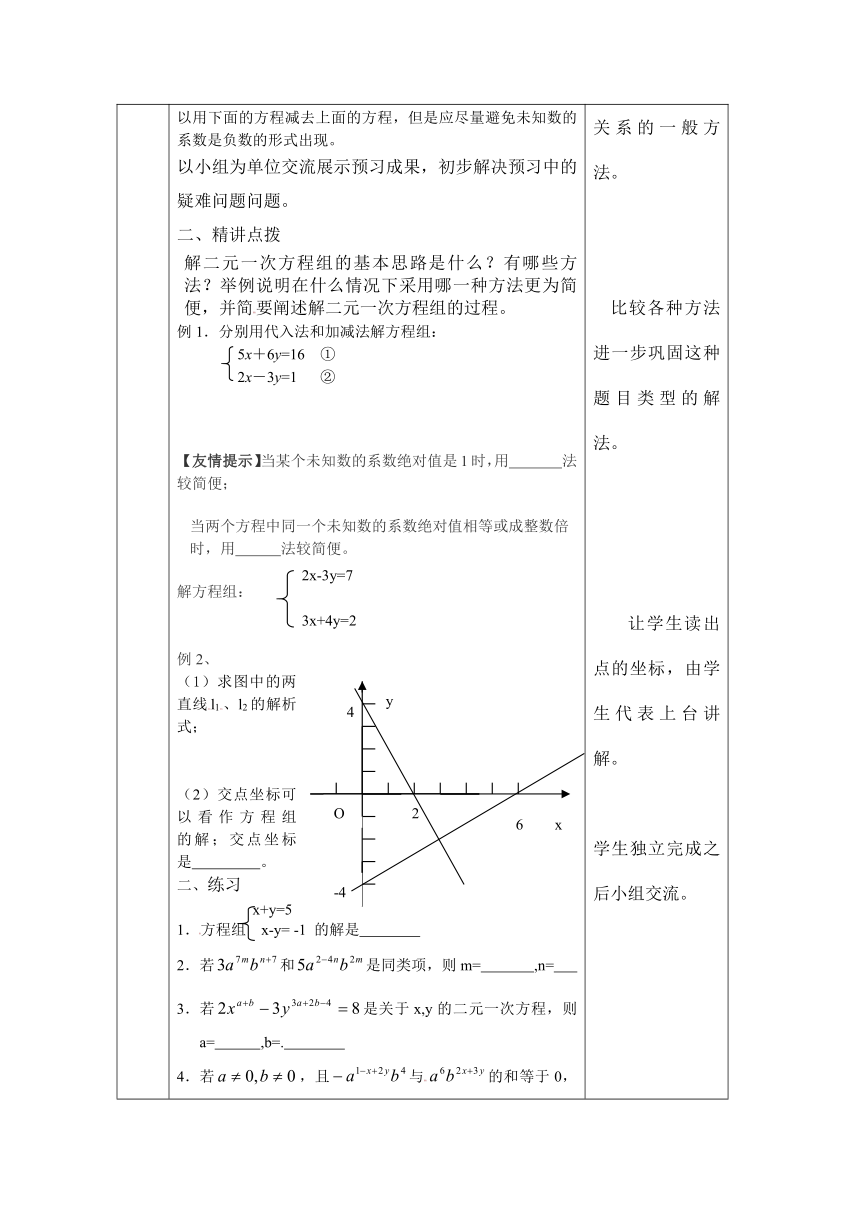
激情导入自主预习⌒指导、尝试、交流︶ 谈自己所记得的知识。一、知识点疏理：1、二元一次方程：含有 个未知数、且 为1，这样的方程叫二元一次方程。2、二元一次方程的解：能使二元一次方程 的值叫做二元一次方程的解，通常用的形式表示。3、二元一次方程组：①由两个二元一次方程组成，常用“{”把这两个方程联合在一起；②整个方程组中含有两个不同的未知数，且方程组中同一未知数代表同一类型的数量；③方程组中的每个方程经过整理后都是一次方程，如等都是二元一次方程组。4、解二元一次方程组的方法是 ， 。5、由于方程组的系数千变万化，因此解题的方法也就有优劣之分，选择什么样的途径去解题时应有“最优策略”的意识，比如解方程组就应该先消去 ，而不是先消去 。6、代入消元法解二元一次方程组的关键是将方程组中的一个方程变形，变为 ，比如把x+2y=1变形为 。在变形的过程中可能要去分母、去括号、移项、系数化为1等，因此变形的过程是易出错的地方，要认真对待。7、如果方程中某个未知数的系数的绝对值相等的话，通常使用 解二元一次方程组。此时，两个方程的左、右两边相加（或相减）时，要注意符号，确保准确无误，尤其是相减时，可以用上面的方程减下面的方程，也可以用下面的方程减去上面的方程，但是应尽量避免未知数的系数是负数的形式出现。以小组为单位交流展示预习成果，初步解决预习中的疑难问题问题。二、精讲点拨解二元一次方程组的基本思路是什么？有哪些方法？举例说明在什么情况下采用哪一种方法更为简便，并简要阐述解二元一次方程组的过程。例1．分别用代入法和加减法解方程组：5x＋6y=16 ①2x－3y=1 ②【友情提示】当某个未知数的系数绝对值是1时，用 法较简便；当两个方程中同一个未知数的系数绝对值相等或成整数倍时，用 法较简便。解方程组：例2、（1）求图中的两直线l1、l2的解析式；（2）交点坐标可以看作方程组 的解；交点坐标是 。二、练习 x+y=5方程组 x-y= -1 的解是 若和是同类项，则m= ,n= 若是关于x,y的二元一次方程，则a= ,b=. 若，且与的和等于0，则x= ,y= 当a ,b 时，方程是关于x,y的二元一次方程。已知 x=5+t 用x的代数式表示y，则y= y+1=3-t已知与互为相反数，则x= ,y= 7、在方程(k2-4)x2+(2-3k)x+(k+1)y+3k=0中，若此方程为二元一次方程，则k值为（ ）A、2 B、-2 C、2或-2 D、以上答案都不对．8、若是二元一次方程组的解，则这个方程组是（ ）A、 B、 C、 D、9、在方程中，用含的代数式表示，则 （ ）A、 B、 C、 D、10、已知ｘ＝３－ｋ，ｙ＝ｋ＋２，则ｙ与ｘ的关系是（ ）Ａ、ｘ＋ｙ＝５　　Ｂ、ｘ＋ｙ＝１　　Ｃ、ｘ－ｙ＝１　　Ｄ、ｙ＝ｘ－１学生独立完成然后小组交流。11、解关于的方程教师提示 12、用代入法解下列方程组（1）13、用加减法解下列方程组（1）学生板演14、某商店出售的某种茶壶每只定价20元，茶杯每只定价3元，该商店在营销淡季特规定一项优惠方法，即买一只茶壶赠送一只茶杯，单位里花了170元，买回茶壶和茶杯一共38只，问单位里买回茶壶和茶杯各多少只？学生讲解。四、小结：本节课学会了什么？ 教师鼓励学生出示复习问题提示，学生先自己预习，小组成员之间交流加以记忆。教师强调：解二元一次方程组时，根据系数确定应该用哪一种方法。 列方程组解应用题找等量关系的一般方法。 比较各种方法进一步巩固这种题目类型的解法。 让学生读出点的坐标，由学生代表上台讲解。学生独立完成之后小组交流。变式训练：平方与绝对值的组合教师强调：二次项系数为0，但是必须保证一次项的存在。学生回答去括号。学生板演互相修改。代表口述等量关系之后板演过程
2x-3y=7
3x+4y=2
x
y
O
2
4
6
-4