2020-2021学年上海市奉贤区五校联考六年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市奉贤区五校联考六年级(下)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 503.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览




文档简介
2020-2021学年上海市奉贤区五校联考六年级(下)期末数学试卷(五四学制)
一、选择题(每题3分,满分18分)
1.在体育课的立定跳远测试中,以2.00m为标准,若小明跳出了2.35m,可记作+0.35m,则小亮跳出了1.75m,应记作( )
A.+0.25m B.﹣0.25m C.+0.35m D.﹣0.35m
2.在数轴上,位于﹣2和2之间的点表示的有理数有( )
A.5个 B.4个 C.3个 D.无数个
3.观察下列方程其中是二元一次方程是( )
A.5x﹣y=35 B.xy=16
C.2x2﹣1=0 D.3z﹣2(z+1)=6
4.已知m<n,那么下列各式中,不一定成立的是( )
A.2m<2n B.3﹣m>3﹣n C.mc2<nc2 D.m﹣3<n﹣1
5.已知A、B两地的位置如图所示,且∠BAC=150°,那么下列语句正确的是( )
A.A地在B地的北偏东60°方向
B.A地在B地的北偏东30°方向
C.B地在A地的北偏东60°方向
D.B地在A地的北偏东30°方向
6.下列说法中,
(1)联结两点的线段叫做两点之间的距离;
(2)用度量法和叠合法都可以比较两个角的大小;
(3)铅垂线、三角尺、合页型折纸都可以检验直线和平面垂直;
(4)六个面、十二条棱和八个顶点组成的图形都是长方体;
你认为正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题:(本大题共12题,每题2分,满分24分)
7.的相反数是 .
8.计算:= .
9.如果|x|=,则x= .
10.比较大小: .
11.现今世界上较先进的计算机显卡每秒可绘制出27 000 000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形 个.
12.将方程2x+y﹣1=0变形为用含有y的式子表示x,则x= .
13.若是方程kx﹣3y=1的一个解,则k= .
14.不等式的3x﹣6≤2+x非负整数解共有 .
15.已知∠A=38°24',则∠A的补角的大小是 .
16.如图,已知BD=16cm,BD=AB,点C是线段BD的中点,那么AC= cm.
17.如图,在长方体ABCD﹣EFGH中,与棱AD异面的棱有 条.
18.本学期我们学习了“有理数的乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.定义:am与an(a≠0,m,n都是正整数)叫做同底数幂,同底数幂除法记作am÷an.其中“同底数幂除法”运算法则中规定当m=n时,am÷an=am﹣n=a0=1,根据“同底数幂除法”法则中的规定和你已经学过的知识,如果等式x2x+4÷xx+7=1成立,则请写出满足等式成立的所有的x的值 .
三、简答题(本大题共5题,每题6分,满分30分)
19.计算:﹣32+|﹣5|﹣18×.
20.解方程:.
21.解方程组:
22.解不等式组:,并将其解集在数轴上表示出来.
23.解方程组:.
四、解答题(第24题6分,第25、26各7分,第27题8分,满分28分)
24.用斜二测画法画长方体直观图:
(1)补全长方体ABCD﹣A1B1C1D1;
(2)量得B1C1的长度是 cm,所表示的实际长度是 cm.
(3)与平面A1ABB1,平行的平面是 .
25.已知线段a、b(如图),根据下列要求,依次画图或计算.
(1)画出一条线段OA,使它等于3a﹣b;
(2)画出线段OA的中点M;
(3)如果a=2.5厘米,b=3厘米,求线段OM的长.
(画图时不要求写出画法,但要保留画图痕迹,及写出结论)
26.目前,新型冠状病毒在我国虽可控可防,但不可松懈,某校欲购置规格分别为300ml和500ml的甲、乙两种免洗手消毒液共400瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶.
(1)如果购买这两种消毒液共7500元,求甲、乙两种消毒液各购买多少瓶?
(2)在(1)的条件下,若该校在校师生共1800人,平均每人每天都需使用10ml的免洗手消毒液,则这批消毒液可使用多少天?
27.已知点O为直线AB上一点.
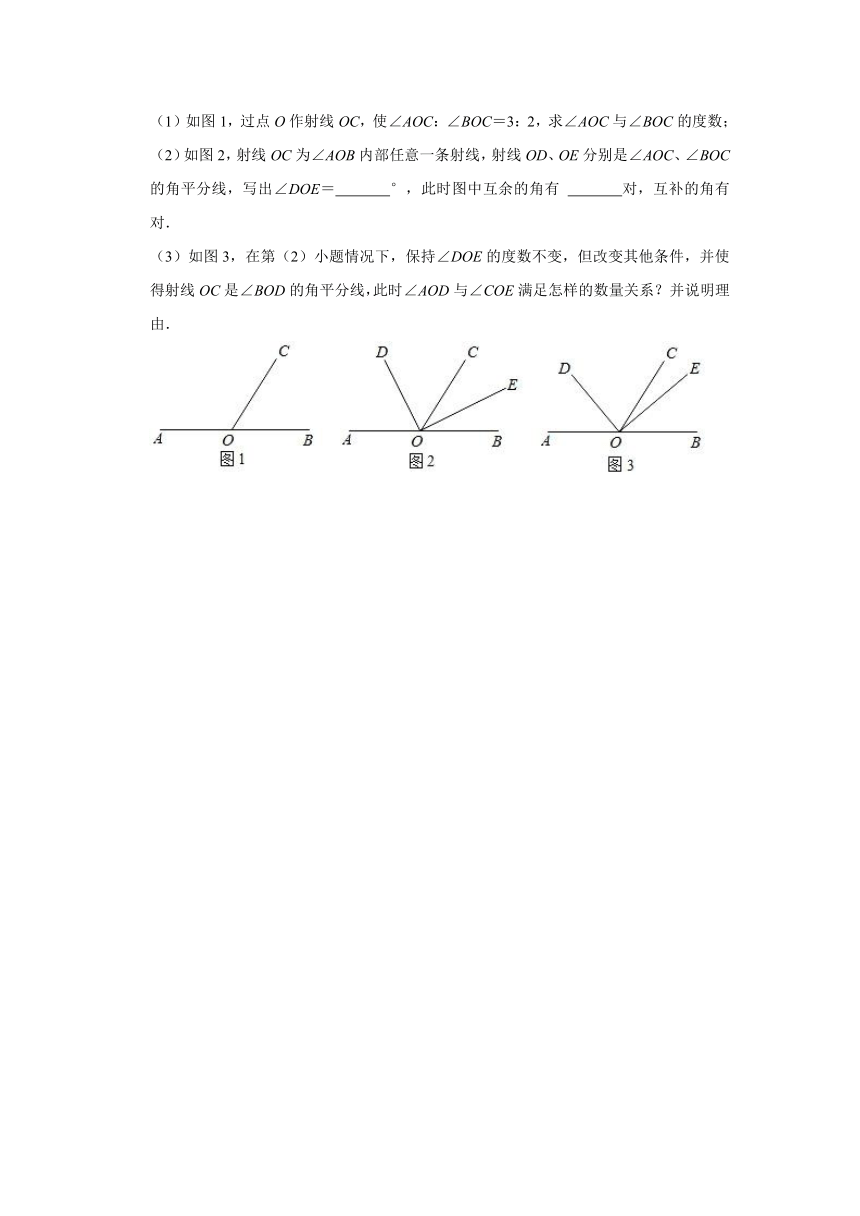
(1)如图1,过点O作射线OC,使∠AOC:∠BOC=3:2,求∠AOC与∠BOC的度数;
(2)如图2,射线OC为∠AOB内部任意一条射线,射线OD、OE分别是∠AOC、∠BOC的角平分线,写出∠DOE= °,此时图中互余的角有 对,互补的角有 对.
(3)如图3,在第(2)小题情况下,保持∠DOE的度数不变,但改变其他条件,并使得射线OC是∠BOD的角平分线,此时∠AOD与∠COE满足怎样的数量关系?并说明理由.
参考答案
一、选择题:(本大题共6题,每题3分,满分18分)
1.在体育课的立定跳远测试中,以2.00m为标准,若小明跳出了2.35m,可记作+0.35m,则小亮跳出了1.75m,应记作( )
A.+0.25m B.﹣0.25m C.+0.35m D.﹣0.35m
解:1.75﹣2.00=﹣0.25,
故小亮跳出了1.75m,应记作﹣0.25m.
故选:B.
2.在数轴上,位于﹣2和2之间的点表示的有理数有( )
A.5个 B.4个 C.3个 D.无数个
解:∵有理数包括整数和分数,
∴在﹣2和2之间的有理数有无数个,如﹣1,0,1,,等等.
故选:D.
3.观察下列方程其中是二元一次方程是( )
A.5x﹣y=35 B.xy=16
C.2x2﹣1=0 D.3z﹣2(z+1)=6
解:A、该方程符合二元一次方程的定义,符合题意.
B、该方程是二元二次方程,不符合题意.
C、该方程是一元二次方程,不符合题意.
D、该方程是一元一次方程,不符合题意.
故选:A.
4.已知m<n,那么下列各式中,不一定成立的是( )
A.2m<2n B.3﹣m>3﹣n C.mc2<nc2 D.m﹣3<n﹣1
解:A、由m<n,根据不等式性质2,得2m<2n,本选项成立;
B、由m<n,根据不等式性质3,得﹣m>﹣n,再根据不等式性质1,得3﹣m>3﹣n,本选项成立;
C、因为c2≥0,当c2>0时,根据不等式性质2,得mc2<nc2,当c2=0时,mc2=nc2,本选项不一定成立;
D、由m<n,根据不等式性质1,得m﹣3<n﹣2<n﹣1,本选项成立;
故选:C.
5.已知A、B两地的位置如图所示,且∠BAC=150°,那么下列语句正确的是( )
A.A地在B地的北偏东60°方向
B.A地在B地的北偏东30°方向
C.B地在A地的北偏东60°方向
D.B地在A地的北偏东30°方向
解:∵∠BAC=150°,
∴∠1=150°﹣90°=60°,
∴B地在A地的北偏东60°方向.
故选:C.
6.下列说法中,
(1)联结两点的线段叫做两点之间的距离;
(2)用度量法和叠合法都可以比较两个角的大小;
(3)铅垂线、三角尺、合页型折纸都可以检验直线和平面垂直;
(4)六个面、十二条棱和八个顶点组成的图形都是长方体;
你认为正确的个数为( )
A.1个 B.2个 C.3个 D.4个
解:A、联结两点的线段的长度叫做两点之间的距离,故选项错误;
B、用度量法和叠合法都可以比较两个角的大小是正确的;
C、铅垂线、三角尺、合页型折纸可以检验直线与平面垂直是正确的;
D、由六个面、十二条棱和八个顶点组成的图形可以是棱台,故选项错误.
故选:B.
二、填空题:(本大题共12题,每题2分,满分24分)
7.的相反数是 .
解:﹣1的相反数是:1.
故答案为:1.
8.计算:= .
解:原式=,
故答案为:﹣.
9.如果|x|=,则x= .
解:因为,
所以x=,
故答案为:.
10.比较大小: > .
解:∵|﹣|=,|﹣2|=,<,
∴﹣>﹣2,
故答案为:>.
11.现今世界上较先进的计算机显卡每秒可绘制出27 000 000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形 2.7×107 个.
解:27 000 000=2.7×107个.
12.将方程2x+y﹣1=0变形为用含有y的式子表示x,则x= .
解:方程2x+y﹣1=0,
解得:x=.
故答案为:.
13.若是方程kx﹣3y=1的一个解,则k= ﹣5 .
解:由题意得:﹣2k﹣3×3=1.
∴k=﹣5.
故答案为:﹣5.
14.不等式的3x﹣6≤2+x非负整数解共有 5 .
解:3x﹣6≤2+x,
3x﹣x≤2+6,
2x≤8,
解得:x≤4,
则不等式的非负整数解为0,1,2,3,4共5个.
故答案为5.
15.已知∠A=38°24',则∠A的补角的大小是 141°36' .
解:∵∠A=38°24',
∴∠A的补角的大小是180°﹣38°24'=141°36',
故答案为:141°36'.
16.如图,已知BD=16cm,BD=AB,点C是线段BD的中点,那么AC= 32 cm.
解:∵BD=16cm,BD=AB,
∴AB=BD=×16=40(cm),
又∵点C是线段BD的中点,
∴BC=BD=8cm,
则AC=AB﹣BC=40﹣8=32(cm),
故答案为:32.
17.如图,在长方体ABCD﹣EFGH中,与棱AD异面的棱有 4 条.
解:棱AD异面的棱:BF、CG、EF、HG,
故答案为:4.
18.本学期我们学习了“有理数的乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.定义:am与an(a≠0,m,n都是正整数)叫做同底数幂,同底数幂除法记作am÷an.其中“同底数幂除法”运算法则中规定当m=n时,am÷an=am﹣n=a0=1,根据“同底数幂除法”法则中的规定和你已经学过的知识,如果等式x2x+4÷xx+7=1成立,则请写出满足等式成立的所有的x的值 3或1 .
解:有两种情况:①当x=1时,x2x+4÷xx+7=16÷18=1,
②(2x+4)﹣(x+7)=0,
解得:x=3,
所以x=3或1,
故答案为:3或1.
三、简答题(本大题共5题,每题6分,满分30分)
19.计算:﹣32+|﹣5|﹣18×.
解:﹣32+|﹣5|﹣18×
=﹣9+5﹣18×
=﹣4﹣2
=﹣6
20.解方程:.
解:去分母得,2(2x﹣1)﹣3(5x+1)﹣6=0,
去括号的,4x﹣2﹣15x﹣3﹣6=0,
移项得,4x﹣15x=2+3+6,
合并同类项得,﹣11x=11,
系数化为1得,x=﹣1.
故答案为:x=﹣1.
21.解方程组:
解:由①得:y=2x﹣8③,
把③代入②得:x=3,
把x=3代入③得:y=﹣2.
所以方程组的解为.
22.解不等式组:,并将其解集在数轴上表示出来.
解:,
由①得,x>﹣2;
由②得,x≤4,
故此不等式组的解集为:﹣2<x≤4.
在数轴上表示为:
.
23.解方程组:.
解:,
①+②得,3x+z=6④
③④组成二元一次方程组得,
解得,
代入①得,y=2,
∴原方程组的解为.
四、解答题(第24题6分,第25、26各7分,第27题8分,满分28分)
24.用斜二测画法画长方体直观图:
(1)补全长方体ABCD﹣A1B1C1D1;
(2)量得B1C1的长度是 1 cm,所表示的实际长度是 2 cm.
(3)与平面A1ABB1,平行的平面是 面C1CDD1 .
解:(1)如图,长方体ABCD﹣A1B1C1D1即为所求.
(2)测量B1C1=1cm,AB=2cm,
∴B1C1的实际长度为2cm.
故答案为:1,2.
(3)与平面A1ABB1,平行的平面是面C1CDD1
故答案为:面C1CDD1.
25.已知线段a、b(如图),根据下列要求,依次画图或计算.
(1)画出一条线段OA,使它等于3a﹣b;
(2)画出线段OA的中点M;
(3)如果a=2.5厘米,b=3厘米,求线段OM的长.
(画图时不要求写出画法,但要保留画图痕迹,及写出结论)
解:(1)如图,OA为所作;
(2)如图,点M为所作;
(3)∵OA=3a﹣b=3×2.5﹣3=4.5(厘米),
而M点为OA的中点,
∴OM=OA=2.25厘米.
26.目前,新型冠状病毒在我国虽可控可防,但不可松懈,某校欲购置规格分别为300ml和500ml的甲、乙两种免洗手消毒液共400瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶.
(1)如果购买这两种消毒液共7500元,求甲、乙两种消毒液各购买多少瓶?
(2)在(1)的条件下,若该校在校师生共1800人,平均每人每天都需使用10ml的免洗手消毒液,则这批消毒液可使用多少天?
解:(1)设甲种消毒液购买了x瓶,乙种消毒液购买了y瓶,
依题意得:,
解得:.
答:甲种消毒液购买了100瓶,乙种消毒液购买了300瓶.
(2)(300×100+500×300)÷(10×1800)=10(天).
答:这批消毒液可使用10天.
27.已知点O为直线AB上一点.
(1)如图1,过点O作射线OC,使∠AOC:∠BOC=3:2,求∠AOC与∠BOC的度数;
(2)如图2,射线OC为∠AOB内部任意一条射线,射线OD、OE分别是∠AOC、∠BOC的角平分线,写出∠DOE= 90 °,此时图中互余的角有 4 对,互补的角有 5 对.
(3)如图3,在第(2)小题情况下,保持∠DOE的度数不变,但改变其他条件,并使得射线OC是∠BOD的角平分线,此时∠AOD与∠COE满足怎样的数量关系?并说明理由.
解:(1)∵∠AOC:∠BOC=3:2,
∴设∠AOC=3x,则∠BOC=2x,
根据题意得:3x+2x=180°,
∴x=36°,
∴∠AOC=180°,∠BOC=72°;
(2)∵射线OD、OE分别是∠AOC、∠BOC的角平分线,
∴∠COD=∠AOC,∠COE=∠BOC,
∴∠DOE=∠COD+∠COE
=(∠AOC+∠BOC)
=×180°
=90°;
∵∠COD+∠COE=90°,∠AOD+∠COE=90°,∠AOD+∠BOE=90°,∠COD+∠BOE=90°,
∴互余的角有4对;
∵∠AOD+∠BOD=180°,∠COD+∠BOD=180°,∠BOE+∠AOE=180°,∠COE+∠AOE=180°,∠AOC+∠BOC=180°,
∴互补的角有5对;
故答案为:90,4,5;
(3)∠AOD=2∠COE.理由如下:
∵射线OC是∠BOD的角平分线,
∴∠BOC=∠BOD=(180°﹣∠AOD)=90°﹣∠AOD,
∵∠AOD+∠DOC+∠BOC=180°,
∴∠AOD+(90°﹣∠COE)+(90°﹣∠AOD)=180°,
∴∠AOD=2∠COE.
一、选择题(每题3分,满分18分)
1.在体育课的立定跳远测试中,以2.00m为标准,若小明跳出了2.35m,可记作+0.35m,则小亮跳出了1.75m,应记作( )
A.+0.25m B.﹣0.25m C.+0.35m D.﹣0.35m
2.在数轴上,位于﹣2和2之间的点表示的有理数有( )
A.5个 B.4个 C.3个 D.无数个
3.观察下列方程其中是二元一次方程是( )
A.5x﹣y=35 B.xy=16
C.2x2﹣1=0 D.3z﹣2(z+1)=6
4.已知m<n,那么下列各式中,不一定成立的是( )
A.2m<2n B.3﹣m>3﹣n C.mc2<nc2 D.m﹣3<n﹣1
5.已知A、B两地的位置如图所示,且∠BAC=150°,那么下列语句正确的是( )
A.A地在B地的北偏东60°方向
B.A地在B地的北偏东30°方向
C.B地在A地的北偏东60°方向
D.B地在A地的北偏东30°方向
6.下列说法中,
(1)联结两点的线段叫做两点之间的距离;
(2)用度量法和叠合法都可以比较两个角的大小;
(3)铅垂线、三角尺、合页型折纸都可以检验直线和平面垂直;
(4)六个面、十二条棱和八个顶点组成的图形都是长方体;
你认为正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题:(本大题共12题,每题2分,满分24分)
7.的相反数是 .
8.计算:= .
9.如果|x|=,则x= .
10.比较大小: .
11.现今世界上较先进的计算机显卡每秒可绘制出27 000 000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形 个.
12.将方程2x+y﹣1=0变形为用含有y的式子表示x,则x= .
13.若是方程kx﹣3y=1的一个解,则k= .
14.不等式的3x﹣6≤2+x非负整数解共有 .
15.已知∠A=38°24',则∠A的补角的大小是 .
16.如图,已知BD=16cm,BD=AB,点C是线段BD的中点,那么AC= cm.
17.如图,在长方体ABCD﹣EFGH中,与棱AD异面的棱有 条.
18.本学期我们学习了“有理数的乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.定义:am与an(a≠0,m,n都是正整数)叫做同底数幂,同底数幂除法记作am÷an.其中“同底数幂除法”运算法则中规定当m=n时,am÷an=am﹣n=a0=1,根据“同底数幂除法”法则中的规定和你已经学过的知识,如果等式x2x+4÷xx+7=1成立,则请写出满足等式成立的所有的x的值 .
三、简答题(本大题共5题,每题6分,满分30分)
19.计算:﹣32+|﹣5|﹣18×.
20.解方程:.
21.解方程组:
22.解不等式组:,并将其解集在数轴上表示出来.
23.解方程组:.
四、解答题(第24题6分,第25、26各7分,第27题8分,满分28分)
24.用斜二测画法画长方体直观图:
(1)补全长方体ABCD﹣A1B1C1D1;
(2)量得B1C1的长度是 cm,所表示的实际长度是 cm.
(3)与平面A1ABB1,平行的平面是 .
25.已知线段a、b(如图),根据下列要求,依次画图或计算.
(1)画出一条线段OA,使它等于3a﹣b;
(2)画出线段OA的中点M;
(3)如果a=2.5厘米,b=3厘米,求线段OM的长.
(画图时不要求写出画法,但要保留画图痕迹,及写出结论)
26.目前,新型冠状病毒在我国虽可控可防,但不可松懈,某校欲购置规格分别为300ml和500ml的甲、乙两种免洗手消毒液共400瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶.
(1)如果购买这两种消毒液共7500元,求甲、乙两种消毒液各购买多少瓶?
(2)在(1)的条件下,若该校在校师生共1800人,平均每人每天都需使用10ml的免洗手消毒液,则这批消毒液可使用多少天?
27.已知点O为直线AB上一点.
(1)如图1,过点O作射线OC,使∠AOC:∠BOC=3:2,求∠AOC与∠BOC的度数;
(2)如图2,射线OC为∠AOB内部任意一条射线,射线OD、OE分别是∠AOC、∠BOC的角平分线,写出∠DOE= °,此时图中互余的角有 对,互补的角有 对.
(3)如图3,在第(2)小题情况下,保持∠DOE的度数不变,但改变其他条件,并使得射线OC是∠BOD的角平分线,此时∠AOD与∠COE满足怎样的数量关系?并说明理由.
参考答案
一、选择题:(本大题共6题,每题3分,满分18分)
1.在体育课的立定跳远测试中,以2.00m为标准,若小明跳出了2.35m,可记作+0.35m,则小亮跳出了1.75m,应记作( )
A.+0.25m B.﹣0.25m C.+0.35m D.﹣0.35m
解:1.75﹣2.00=﹣0.25,
故小亮跳出了1.75m,应记作﹣0.25m.
故选:B.
2.在数轴上,位于﹣2和2之间的点表示的有理数有( )
A.5个 B.4个 C.3个 D.无数个
解:∵有理数包括整数和分数,
∴在﹣2和2之间的有理数有无数个,如﹣1,0,1,,等等.
故选:D.
3.观察下列方程其中是二元一次方程是( )
A.5x﹣y=35 B.xy=16
C.2x2﹣1=0 D.3z﹣2(z+1)=6
解:A、该方程符合二元一次方程的定义,符合题意.
B、该方程是二元二次方程,不符合题意.
C、该方程是一元二次方程,不符合题意.
D、该方程是一元一次方程,不符合题意.
故选:A.
4.已知m<n,那么下列各式中,不一定成立的是( )
A.2m<2n B.3﹣m>3﹣n C.mc2<nc2 D.m﹣3<n﹣1
解:A、由m<n,根据不等式性质2,得2m<2n,本选项成立;
B、由m<n,根据不等式性质3,得﹣m>﹣n,再根据不等式性质1,得3﹣m>3﹣n,本选项成立;
C、因为c2≥0,当c2>0时,根据不等式性质2,得mc2<nc2,当c2=0时,mc2=nc2,本选项不一定成立;
D、由m<n,根据不等式性质1,得m﹣3<n﹣2<n﹣1,本选项成立;
故选:C.
5.已知A、B两地的位置如图所示,且∠BAC=150°,那么下列语句正确的是( )
A.A地在B地的北偏东60°方向
B.A地在B地的北偏东30°方向
C.B地在A地的北偏东60°方向
D.B地在A地的北偏东30°方向
解:∵∠BAC=150°,
∴∠1=150°﹣90°=60°,
∴B地在A地的北偏东60°方向.
故选:C.
6.下列说法中,
(1)联结两点的线段叫做两点之间的距离;
(2)用度量法和叠合法都可以比较两个角的大小;
(3)铅垂线、三角尺、合页型折纸都可以检验直线和平面垂直;
(4)六个面、十二条棱和八个顶点组成的图形都是长方体;
你认为正确的个数为( )
A.1个 B.2个 C.3个 D.4个
解:A、联结两点的线段的长度叫做两点之间的距离,故选项错误;
B、用度量法和叠合法都可以比较两个角的大小是正确的;
C、铅垂线、三角尺、合页型折纸可以检验直线与平面垂直是正确的;
D、由六个面、十二条棱和八个顶点组成的图形可以是棱台,故选项错误.
故选:B.
二、填空题:(本大题共12题,每题2分,满分24分)
7.的相反数是 .
解:﹣1的相反数是:1.
故答案为:1.
8.计算:= .
解:原式=,
故答案为:﹣.
9.如果|x|=,则x= .
解:因为,
所以x=,
故答案为:.
10.比较大小: > .
解:∵|﹣|=,|﹣2|=,<,
∴﹣>﹣2,
故答案为:>.
11.现今世界上较先进的计算机显卡每秒可绘制出27 000 000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形 2.7×107 个.
解:27 000 000=2.7×107个.
12.将方程2x+y﹣1=0变形为用含有y的式子表示x,则x= .
解:方程2x+y﹣1=0,
解得:x=.
故答案为:.
13.若是方程kx﹣3y=1的一个解,则k= ﹣5 .
解:由题意得:﹣2k﹣3×3=1.
∴k=﹣5.
故答案为:﹣5.
14.不等式的3x﹣6≤2+x非负整数解共有 5 .
解:3x﹣6≤2+x,
3x﹣x≤2+6,
2x≤8,
解得:x≤4,
则不等式的非负整数解为0,1,2,3,4共5个.
故答案为5.
15.已知∠A=38°24',则∠A的补角的大小是 141°36' .
解:∵∠A=38°24',
∴∠A的补角的大小是180°﹣38°24'=141°36',
故答案为:141°36'.
16.如图,已知BD=16cm,BD=AB,点C是线段BD的中点,那么AC= 32 cm.
解:∵BD=16cm,BD=AB,
∴AB=BD=×16=40(cm),
又∵点C是线段BD的中点,
∴BC=BD=8cm,
则AC=AB﹣BC=40﹣8=32(cm),
故答案为:32.
17.如图,在长方体ABCD﹣EFGH中,与棱AD异面的棱有 4 条.
解:棱AD异面的棱:BF、CG、EF、HG,
故答案为:4.
18.本学期我们学习了“有理数的乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.定义:am与an(a≠0,m,n都是正整数)叫做同底数幂,同底数幂除法记作am÷an.其中“同底数幂除法”运算法则中规定当m=n时,am÷an=am﹣n=a0=1,根据“同底数幂除法”法则中的规定和你已经学过的知识,如果等式x2x+4÷xx+7=1成立,则请写出满足等式成立的所有的x的值 3或1 .
解:有两种情况:①当x=1时,x2x+4÷xx+7=16÷18=1,
②(2x+4)﹣(x+7)=0,
解得:x=3,
所以x=3或1,
故答案为:3或1.
三、简答题(本大题共5题,每题6分,满分30分)
19.计算:﹣32+|﹣5|﹣18×.
解:﹣32+|﹣5|﹣18×
=﹣9+5﹣18×
=﹣4﹣2
=﹣6
20.解方程:.
解:去分母得,2(2x﹣1)﹣3(5x+1)﹣6=0,
去括号的,4x﹣2﹣15x﹣3﹣6=0,
移项得,4x﹣15x=2+3+6,
合并同类项得,﹣11x=11,
系数化为1得,x=﹣1.
故答案为:x=﹣1.
21.解方程组:
解:由①得:y=2x﹣8③,
把③代入②得:x=3,
把x=3代入③得:y=﹣2.
所以方程组的解为.
22.解不等式组:,并将其解集在数轴上表示出来.
解:,
由①得,x>﹣2;
由②得,x≤4,
故此不等式组的解集为:﹣2<x≤4.
在数轴上表示为:
.
23.解方程组:.
解:,
①+②得,3x+z=6④
③④组成二元一次方程组得,
解得,
代入①得,y=2,
∴原方程组的解为.
四、解答题(第24题6分,第25、26各7分,第27题8分,满分28分)
24.用斜二测画法画长方体直观图:
(1)补全长方体ABCD﹣A1B1C1D1;
(2)量得B1C1的长度是 1 cm,所表示的实际长度是 2 cm.
(3)与平面A1ABB1,平行的平面是 面C1CDD1 .
解:(1)如图,长方体ABCD﹣A1B1C1D1即为所求.
(2)测量B1C1=1cm,AB=2cm,
∴B1C1的实际长度为2cm.
故答案为:1,2.
(3)与平面A1ABB1,平行的平面是面C1CDD1
故答案为:面C1CDD1.
25.已知线段a、b(如图),根据下列要求,依次画图或计算.
(1)画出一条线段OA,使它等于3a﹣b;
(2)画出线段OA的中点M;
(3)如果a=2.5厘米,b=3厘米,求线段OM的长.
(画图时不要求写出画法,但要保留画图痕迹,及写出结论)
解:(1)如图,OA为所作;
(2)如图,点M为所作;
(3)∵OA=3a﹣b=3×2.5﹣3=4.5(厘米),
而M点为OA的中点,
∴OM=OA=2.25厘米.
26.目前,新型冠状病毒在我国虽可控可防,但不可松懈,某校欲购置规格分别为300ml和500ml的甲、乙两种免洗手消毒液共400瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶.
(1)如果购买这两种消毒液共7500元,求甲、乙两种消毒液各购买多少瓶?
(2)在(1)的条件下,若该校在校师生共1800人,平均每人每天都需使用10ml的免洗手消毒液,则这批消毒液可使用多少天?
解:(1)设甲种消毒液购买了x瓶,乙种消毒液购买了y瓶,
依题意得:,
解得:.
答:甲种消毒液购买了100瓶,乙种消毒液购买了300瓶.
(2)(300×100+500×300)÷(10×1800)=10(天).
答:这批消毒液可使用10天.
27.已知点O为直线AB上一点.
(1)如图1,过点O作射线OC,使∠AOC:∠BOC=3:2,求∠AOC与∠BOC的度数;
(2)如图2,射线OC为∠AOB内部任意一条射线,射线OD、OE分别是∠AOC、∠BOC的角平分线,写出∠DOE= 90 °,此时图中互余的角有 4 对,互补的角有 5 对.
(3)如图3,在第(2)小题情况下,保持∠DOE的度数不变,但改变其他条件,并使得射线OC是∠BOD的角平分线,此时∠AOD与∠COE满足怎样的数量关系?并说明理由.
解:(1)∵∠AOC:∠BOC=3:2,
∴设∠AOC=3x,则∠BOC=2x,
根据题意得:3x+2x=180°,
∴x=36°,
∴∠AOC=180°,∠BOC=72°;
(2)∵射线OD、OE分别是∠AOC、∠BOC的角平分线,
∴∠COD=∠AOC,∠COE=∠BOC,
∴∠DOE=∠COD+∠COE
=(∠AOC+∠BOC)
=×180°
=90°;
∵∠COD+∠COE=90°,∠AOD+∠COE=90°,∠AOD+∠BOE=90°,∠COD+∠BOE=90°,
∴互余的角有4对;
∵∠AOD+∠BOD=180°,∠COD+∠BOD=180°,∠BOE+∠AOE=180°,∠COE+∠AOE=180°,∠AOC+∠BOC=180°,
∴互补的角有5对;
故答案为:90,4,5;
(3)∠AOD=2∠COE.理由如下:
∵射线OC是∠BOD的角平分线,
∴∠BOC=∠BOD=(180°﹣∠AOD)=90°﹣∠AOD,
∵∠AOD+∠DOC+∠BOC=180°,
∴∠AOD+(90°﹣∠COE)+(90°﹣∠AOD)=180°,
∴∠AOD=2∠COE.
同课章节目录
