1.2.1 函数的概念 导学案
文档属性
| 名称 | 1.2.1 函数的概念 导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 270.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 13:20:25 | ||
图片预览




文档简介
1.2 函数及其表示
1.2.1 函数的概念
Q
某人到一个水果店去买西瓜,价格表上写的是:6斤以下,每斤0.4元,6斤以上9斤以下,每斤0.5元;9斤以上,每斤0.6元.此人挑了一个西瓜,称重后店主说5元1角,1角就不要了,给5元吧.可这位聪明的顾客马上说,你不仅没少要,反而多收了我的钱.当顾客讲出理由,店主只好承认了错误,照实收了钱.同学们,你知道顾客是怎么晓得店主骗人的吗?
X
1.函数的概念
定义
设A、B是非空的__数集__,如果按照某种确定的对应关系f,使对于集合A中的__任意一个数x__,在集合B中都有__唯一确定__的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数
三要素
对应关系
y=f(x),x∈A
定义域
__x__的取值集合
值域
与x的值相对应的y的值的集合{f(x)|x∈A}.
[知识点拨] (1)对数集的要求:集合A、B为非空数集.
(2)任意性和唯一性:集合A中的数具有任意性,集合B中的数具有唯一性.
(3)对符号“f”的认识:它表示对应关系,在不同的函数中f的具体含义不一样.
(4)一个区别:f(x)是一个符号,不表示f与x的乘积,而f(a)表示函数f(x)当自变量x取a时的一个函数值.
(5)函数三要素:定义域、对应关系和值域是函数的三要素,三者缺一不可.
2.区间及有关概念
(1)一般区间的表示.
设a,b∈R,且a定义
名称
符号
数轴表示
{x|a≤x≤b}
闭区间
__[a,b]__
{x|a<x<b}
开区间
__(a,b)__
{x|a≤x<b}
半开半
闭区间
[a,b)
{x|a<x≤b}
半开半
闭区间
(a,b]
(2)特殊区间的表示.
定义
R
{x|x≥a}
{x|x>a}
{x|x≤a}
{x|x符号
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
[知识点拨] (1)关注实心点、空心圈:用数轴表示区间时,用实心点表示包括在区间内的端点,用空心圈表示不包括在区间内的端点.
(2)区分开和闭:在用区间表示集合时,开和闭不能混淆.
(3)正确理解“∞”:“∞”是一个趋向符号,不是一个数,它表示数的变化趋势.以“-∞”和“+∞”为区间的一端时,这一端点必须用小括号.
Y
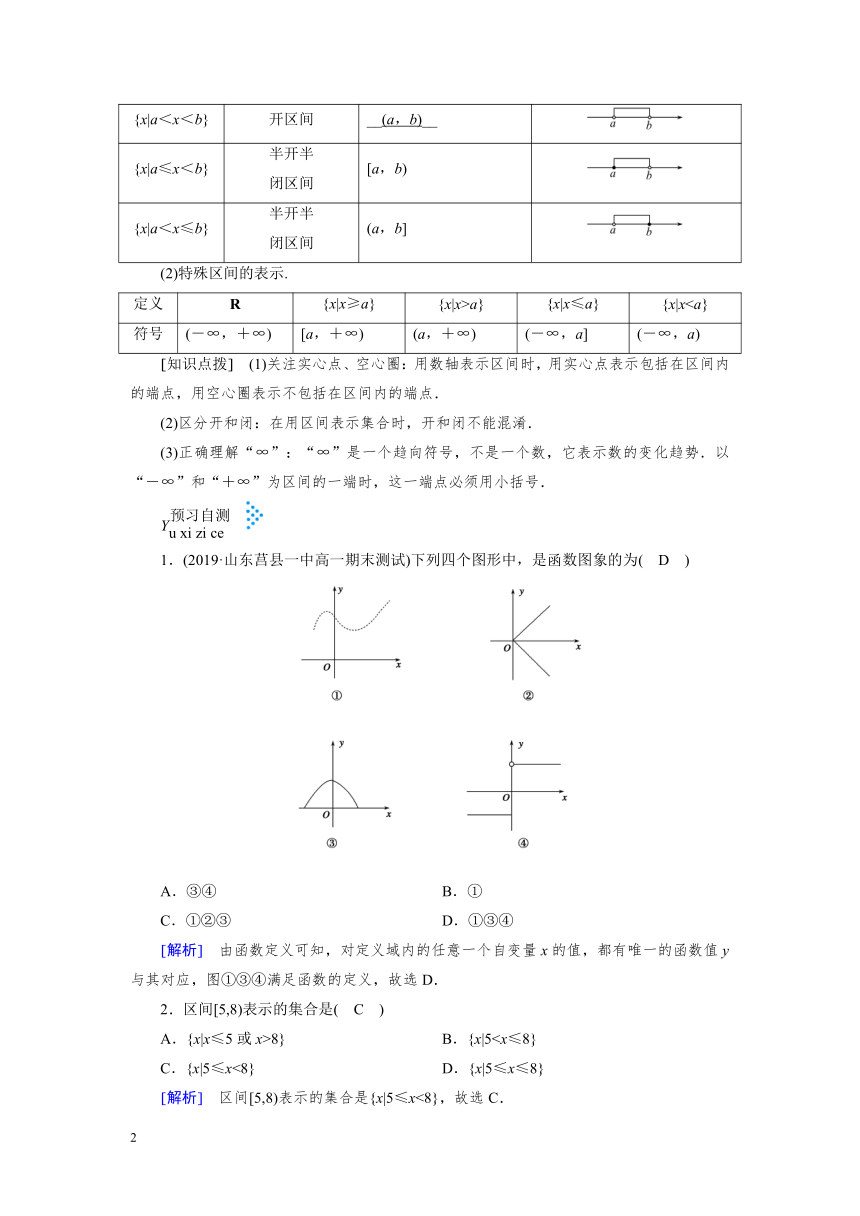
1.(2019·山东莒县一中高一期末测试)下列四个图形中,是函数图象的为( D )
A.③④
B.①
C.①②③
D.①③④
[解析] 由函数定义可知,对定义域内的任意一个自变量x的值,都有唯一的函数值y与其对应,图①③④满足函数的定义,故选D.
2.区间[5,8)表示的集合是( C )
A.{x|x≤5或x>8}
B.{x|5C.{x|5≤x<8}
D.{x|5≤x≤8}
[解析] 区间[5,8)表示的集合是{x|5≤x<8},故选C.
3.已知f(x)=2x+1,则f(5)=( C )
A.3
B.7
C.11
D.25
[解析] f(5)=2×5+1=11,故选C.
4.(2019·江苏,4)函数y=的定义域是__[-1,7]__.
[解析] 要使函数y=有意义,应满足7+6x-x2≥0,
∴x2-6x-7≤0,∴(x-7)(x+1)≤0,
∴-1≤x≤7,
∴函数y=的定义域是[-1,7].
5.已知f(x)=,g(x)=x2+2.
(1)求f(2),g(2)的值;
(2)求f[g(2)]的值;
(3)求f[g(x)]的解析式.
[解析] (1)f(2)==,g(2)=22+2=6.
(2)f[g(2)]===.
(3)f[g(x)]===.
H
命题方向1 ?函数概念的理解
典例1 (1)下列对应或关系式中是A到B的函数的是( B )
A.A∈R,B∈R,x2+y2=1
B.A={1,2,3,4},B={0,1},对应关系如图:
C.A=R,B=R,f:x→y=
D.A=Z,B=Z,f:x→y=
(2)设M={x|-2≤x≤2},N={y|0≤y≤2},函数y=f(x)的定义域为M,值域为N,对于下列四个图象,不可作为函数y=f(x)的图象的是( C )
[思路分析] (1)如何利用函数定义.对于集合A中的元素通过对应关系在集合B中有唯一元素与之对应进行判断.
(2)当对应关系用图象表示时,怎样判断是否为函数关系.
[解析] (1)对于A项,x2+y2=1可化为y=±,显然对任x∈A,y值不唯一,故不符合.对于B项,符合函数的定义.对于C项,2∈A,但在集合B中找不到与之相对应的数,故不符合.对于D项,-1∈A,但在集合B中找不到与之相对应的数,故不符合.
(2)由函数定义可知,任意作一条直线x=a,则与函数的图象至多有一个交点,结合选项可知C中图象不表示y是x的函数.
『规律方法』 1.判断一个对应关系是否是函数,要从以下三个方面去判断,即A,B必须是非空数集;A中任何一个元素在B中必须有元素与其对应;A中任一元素在B中必有唯一元素与其对应.
2.函数的定义中“任一x”与“有唯一确定的y”说明函数中两变量x,y的对应关系是“一对一”或者是“多对一”而不能是“一对多”.
〔跟踪练习1〕
下列对应是否为A到B的函数:
(1)A=R,B={x|x>0},f:x→y=|x|;
(2)A=Z,B=Z,f:x→y=x2;
(3)A=Z,B=Z,f:x→y=;
(4)A=[-1,1],B={0},f:x→y=0.
[解析] (1)A中的元素0在B中没有对应元素,故不是A到B的函数;
(2)对于集合A中的任意一个整数x,按照对应关系f:x→y=x2,在集合B中都有唯一一个确定的整数x2与之对应,故是集合A到集合B的函数;
(3)A中元素负整数没有平方根,故在B中没有对应的元素,故此对应不是A到B的函数;
(4)对于集合A中一个实数x,按照对应关系f:x→y=0,在集合B中都有唯一一个确定的数0与之对应故是集合A到集合B的函数.
命题方向2 ?求函数的定义域
典例2 求下列函数的定义域:
(1)y=;
(2)f(x)=-.
[思路分析] →→
[解析] (1)要使函数有意义,自变量x的取值必须满足,即,解得x<0,且x≠-2.
故原函数的定义域为(-∞,-2)∪(-2,0).
(2)要使函数有意义,自变量x的取值必须满足,即.
故原函数的定义域为(-∞,1)∪(1,4].
『规律方法』 求函数的定义域:
(1)要明确使各函数表达式有意义的条件是什么,函数有意义的准则一般有:①分式的分母不为0;②偶次根式的被开方数非负;③y=x0要求x≠0.
(2)当一个函数由两个或两个以上代数式的和、差、积、商的形式构成时,定义域是使得各式子都有意义的公共部分的集合.
(3)定义域是一个集合,要用集合或区间表示,若用区间表示数集,不能用“或”连接,而应该用并集符号“∪”连接.
〔跟踪练习2〕
(2019·吉林乾安七中高一期末测试)函数y=的定义域是( C )
A.[-1,+∞)
B.[-1,0]
C.(-1,+∞)
D.(-1,0)
[解析] 要使函数y=有意义,应满足x+1>0,∴x>-1,
∴函数y=的定义域为(-1,+∞).
命题方向3 ?求函数值
典例3 (2019·安徽合肥高一期末测试)已知f(x)=,x∈R.
(1)求f(2),f(),f(3),f()的值;
(2)求f(2)+f(3)+…+f(2
018)+f()+f()+…+f()的值.
[思路分析] (1)将x=2,,3,代入f(x)=计算即可;
(2)由(1)中求得f(2),f(),f(3),f()的值可得f(2)+f()与f(3)+f()的值是定值这一规律,再求得f(2)+f(3)+…+f(2
018)+f()+f()+…+f()的值.
[解析] (1)∵f(x)=,
∴f(2)==,f()==,f(3)==,f()==.
(2)由(1)知,
f(2)+f()=1,f(3)+f()=1.
∴f(a)+f()=+=+·=+=1,
∴f(2)+f(3)+…+f(2
018)+f()+f()+…+f()
=f(2)+f()+f(3)+f()+…+f(2
018)+f()
=2
017.
『规律方法』 解题时要注意审题,观察分析、发现规律.
〔跟踪练习3〕已知函数f(x)=,则f(1)++…+=__-9__.
[解析] ===-1,
∴==…==-1,
又∵f(1)=0,
∴f(1)++…+=-9.
Y 求函数定义域时非等价化简解析式而致误
典例4 求函数y=·的定义域.
[错解] y=·=,由x2-4≥0,得x≥2或x≤-2.∴函数的定义域为{x|x≥2或x≤-2}.
[错因分析] 事实上,函数y=·与y=并不表示同一个函数,求函数定义域应根据原始条件的制约.
[正解] 由,得.即x≥2.∴函数的定义域为{x|x≥2}.
X 求函数值域的方法——转化与化归思想及数形结合思想的应用
1.分离常数法
典例5 求函数y=的值域.
[思路分析] 这种求函数值域的问题,我们常把它们化为y=a+的形式再求函数的值域.
[解析] ∵y===3+,
又∵≠0,∴y≠3.∴函数y=的值域是{y|y∈R,且y≠3}.
『规律方法』 求y=这种类型的函数的值域,应采用分离常数法,将函数化为y=a+的形式.
2.配方法
典例6 求函数y=-x2-2x+3(-5≤x≤-2)的值域.
[思路分析] 这种题型,我们常利用配方法把它们化成y=a(x+b)2+c的形式来求函数的值域.
[解析] ∵y=-x2-2x+3=-(x+1)2+4,x∈[-5,-2],
∴其图象是开口向下,顶点为(-1,4),在x∈[-5,-2]上对应的抛物线上的一段弧.
根据x∈[-5,-2]时的抛物线上升,则当x=-5时,y取最小值,且ymin=-12;当x=-2时,y取最大值,且ymax=3.
故y=-x2-2x+3(-5≤x≤-2)的值域是[-12,3].
『规律方法』 遇到求解一般二次函数y=ax2+bx+c(a≠0)的值域时,应采用配方法,将函数化为y=a(x+)2+的形式,从而求得函数的值域.
3.换元法
典例7 求函数y=x+的值域.
[思路分析] 忽略常数系数,则x与隐含二次关系,若令=t,则x=(t2+1),于是函数转化为以t为自变量的二次函数,由于原函数的定义域由有意义确定,故t的允许取值范围就是的取值范围.
[解析] 设u=(x≥),则x=(u≥0),
于是y=+u=(u≥0).由u≥0知(u+1)2≥1,则y≥.
故函数y=x+的值域为[,+∞).
『规律方法』 求解带根号且被开方式为一次式的函数的值域,直接求解很困难,既费时又费力,所以遇到这样的问题,我们要想到用一个字母代换掉带根号的式子.值得注意的是,在代换过程中,要注意新变量的取值范围.
K
1.下列表格中的x与y能构成函数的是( C )
A.
x
非负数
非正数
y
1
-1
B.
x
奇数
0
偶数
y
1
0
-1
C.
x
有理数
无理数
y
1
-1
D.
x
自然数
整数
有理数
y
1
0
-1
[解析] A中,0既是非负数又是非正数;B中,0又是偶数;D中,自然数也是整数,也是有理数,故选C.
2.(2019·山东莒县一中高一期末测试)下列各组函数中,表示同一函数的是( A )
A.y=x与y=
B.y=x2与y=
C.y=1与y=(x-1)0
D.y=|x|与y=()2
[解析] 选项B、C、D中两函数的定义域不同,只有A中的两函数是同一函数.
3.(2019·江苏苏州市高一期末测试)函数f(x)=的定义域为( D )
A.(1,+∞)
B.[1,+∞)
C.[1,2)
D.[1,2)∪(2,+∞)
[解析] 要使函数有意义,应满足,
∴x≥1且x≠2,故选D.
4.(2019·安徽合肥众兴中学高一期末测试)已知f(x)=2x+3,f(m)=6,则m=____.
[解析] ∵f(x)=2x+3,∴f(m)=2m+3=6,
∴2m=3,∴m=.
5.已知函数f(x)=2x+a,g(x)=(x2+3),若g[f(x)]=x2+x+1,求a的值.
[解析] ∵f(x)=2x+a,g(x)=(x2+3),
∴g[f(x)]=g(2x+a)=[(2x+a)2+3]
=x2+ax+(a2+3).
又∵g[f(x)]=x2+x+1,
∴x2+ax+(a2+3)=x2+x+1,
故a=1.
A级 基础巩固
一、选择题
1.下列四种说法中,不正确的是( B )
A.在函数值域中的每一个数,在定义域中都至少有一个数与之对应
B.函数的定义域和值域一定是无限集合
C.定义域和对应关系确定后,函数的值域也就确定了
D.若函数的定义域中只含有一个元素,则值域也只含有一个元素
[解析] 由函数定义域、值域、对应关系的相关知识,易知选B.
2.已知区间,则实数a满足的条件是( D )
A.a∈R
B.a≤-1
C.a≥-1
D.a>-1
[解析] 由题意得2a+1>a,∴a>-1,故选D.
3.函数y=2x+1,x∈N
,且2≤x≤4,则函数的值域是( C )
A.(5,9)
B.[5,0]
C.{5,7,9}
D.{5,6,7,8,9}
[解析] 由题意,函数的定义域为{2,3,4},当x=2时,y=5;当x=3时,y=7;当x=4时,y=9,所以函数的值域为{5,7,9}.
4.集合A={x|0≤x≤4},B={y|0≤y≤2},下列不表示从A到B的函数是( C )
A.f:x→y=x
B.f:x→y=x
C.f:x→y=x
D.f:
x→y=
[解析] 对于选项C,当x=4时,y=>2不合题意.故选C.
5.函数f(x)对于任意实数x满足f(x+2)=,若f(1)=-5,则f[f(5)]=( C )
A.2
B.5
C.-5
D.-
[解析] ∵f(x+2)=,∴f(x)=,
∴f(1)==-5,∴f(3)=-.
∴f(5)==-5.
6.函数y=f(x)的图象与直线x=m的交点个数为( C )
A.可能有无数个
B.只有一个
C.至多一个
D.至少一个
[解析] 根据函数定义,一个自变量x只能对应一个函数值y,而y=f(x)的定义域中不一定含有m.
二、填空题
7.已知函数f(x)=,又知f(t)=6,则t=__-__.
[解析] f(t)==6.∴t=-.
8.已知f(x)=2x-1,则f[f(2)]=__5__.
[解析] ∵f(x)=2x-1,∴f(2)=2×2-1=3,
∴f[f(2)]=f(3)=2×3-1=5.
三、解答题
9.求下列函数的定义域:
(1)f(x)=;
(2)f(x)=;
(3)f(x)=+.
[解析] (1)要使函数有意义,须使x+2≠0,
∴x≠-2,∴函数f(x)的定义域为{x|x≠-2}.
(2)要使函数有意义,须使3x+2≥0,∴x≥-,
∴函数f(x)的定义域为{x|x≥-}.
(3)要使函数有意义,须使,∴x≥-1且x≠3,∴函数f(x)的定义域为{x|x≥-1且x≠3}.
B级 素养提升
一、选择题
1.设函数f(x)=3x2-1,则f(a)-f(-a)的值是( A )
A.0
B.3a2-1
C.6a2-2
D.6a2
[解析] ∵f(x)=3x2-1,
∴f(a)-f(-a)=3a2-1-[3(-a)2-1]=3a2-1-3a2+1=0.
2.A={x|0≤x≤2},B={y|1≤y≤2},下列图形中能表示以A为定义域,B为值域的函数的是( B )
[解析] A、C、D的值域都不是[1,2],故选B.
3.函数f(x)=的定义域为M,g(x)=的定义域为N,则M∩N=( B )
A.[-1,+∞)
B.[-1,)
C.(-1,)
D.(-∞,)
[解析] ∵M={x|x<},N={x|x≥-1},
∴M∩N={x|-1≤x<}.
故选B.
4.已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:则方程g[f(x)]=x的解集为( C )
x
1
2
3
f(x)
2
3
1
x
1
2
3
g(x)
3
2
1
A.{1}
B.{2}
C.{3}
D.?
[解析] 由题意可知,当x=1时,g[f(1)]=g(2)=2,不满足方程;
当x=2时,g[f(2)]=g(3)=1,不满足方程;
当x=3时,g[f(3)]=g(1)=3,满足方程,故选C.
二、填空题
5.若函数f(x)=ax2-1,a为正常数,且f[f(-1)]=-1,则a的值是__1__.
[解析] f(-1)=a-1,∴f[f(-1)]=f(a-1)=a(a-1)2-1=-1,
∴a(a-1)2=0,
又∵a>0,∴(a-1)2=0,∴a=1.
6.函数y=(1≤x≤3)的值域为__[,8]__.
[解析] ∵1≤x≤3,∴1≤x2≤9,
∴≤≤1,
∴≤≤8,
∴函数y=(1≤x≤3)的值域为[,8].
三、解答题
7.已知函数f(x)=x+.
(1)求f(x)的定义域;
(2)求f(-1),f(2)的值;
(3)当a≠-1时,求f(a+1)的值.
[解析] (1)要使函数有意义,必须使x≠0,
∴f(x)的定义域是(-∞,0)∪(0,+∞).
(2)f(-1)=-1+=-2,f(2)=2+=.
(3)当a≠-1时,a+1≠0,∴f(a+1)=a+1+.
8.已知f(x)=x+1,g(x)=x2,求f[g(x)],g[f(x)].
[解析] ∵f(x)=x+1,g(x)=x2,
∴f[g(x)]=f(x2)
=x2+1.
g[f(x)]=g(x+1)=(x+1)2=x2+2x+1.
9.已知函数f(x)=x2-x+,是否存在实数m,使得该函数在x∈[1,m]时,f(x)的取值范围也是[1,m](m>1)?若存在,求出m的值;若不存在,请说明理由.
[解析] f(x)=x2-x+=(x-1)2+1的图象是一条抛物线,它的对称轴为直线x=1,顶点坐标为(1,1),开口向上,若存在实数m,使该函数在x∈[1,m]时,f(x)的取值范围也是[1,m],则需m>1,且f(m)=m,
即m2-m+=m,即m2-4m+3=0,
解得m=3或m=1(舍去m=1).
故存在实数m=3满足条件.
1.2.1 函数的概念
Q
某人到一个水果店去买西瓜,价格表上写的是:6斤以下,每斤0.4元,6斤以上9斤以下,每斤0.5元;9斤以上,每斤0.6元.此人挑了一个西瓜,称重后店主说5元1角,1角就不要了,给5元吧.可这位聪明的顾客马上说,你不仅没少要,反而多收了我的钱.当顾客讲出理由,店主只好承认了错误,照实收了钱.同学们,你知道顾客是怎么晓得店主骗人的吗?
X
1.函数的概念
定义
设A、B是非空的__数集__,如果按照某种确定的对应关系f,使对于集合A中的__任意一个数x__,在集合B中都有__唯一确定__的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数
三要素
对应关系
y=f(x),x∈A
定义域
__x__的取值集合
值域
与x的值相对应的y的值的集合{f(x)|x∈A}.
[知识点拨] (1)对数集的要求:集合A、B为非空数集.
(2)任意性和唯一性:集合A中的数具有任意性,集合B中的数具有唯一性.
(3)对符号“f”的认识:它表示对应关系,在不同的函数中f的具体含义不一样.
(4)一个区别:f(x)是一个符号,不表示f与x的乘积,而f(a)表示函数f(x)当自变量x取a时的一个函数值.
(5)函数三要素:定义域、对应关系和值域是函数的三要素,三者缺一不可.
2.区间及有关概念
(1)一般区间的表示.
设a,b∈R,且a
名称
符号
数轴表示
{x|a≤x≤b}
闭区间
__[a,b]__
{x|a<x<b}
开区间
__(a,b)__
{x|a≤x<b}
半开半
闭区间
[a,b)
{x|a<x≤b}
半开半
闭区间
(a,b]
(2)特殊区间的表示.
定义
R
{x|x≥a}
{x|x>a}
{x|x≤a}
{x|x
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
[知识点拨] (1)关注实心点、空心圈:用数轴表示区间时,用实心点表示包括在区间内的端点,用空心圈表示不包括在区间内的端点.
(2)区分开和闭:在用区间表示集合时,开和闭不能混淆.
(3)正确理解“∞”:“∞”是一个趋向符号,不是一个数,它表示数的变化趋势.以“-∞”和“+∞”为区间的一端时,这一端点必须用小括号.
Y
1.(2019·山东莒县一中高一期末测试)下列四个图形中,是函数图象的为( D )
A.③④
B.①
C.①②③
D.①③④
[解析] 由函数定义可知,对定义域内的任意一个自变量x的值,都有唯一的函数值y与其对应,图①③④满足函数的定义,故选D.
2.区间[5,8)表示的集合是( C )
A.{x|x≤5或x>8}
B.{x|5
D.{x|5≤x≤8}
[解析] 区间[5,8)表示的集合是{x|5≤x<8},故选C.
3.已知f(x)=2x+1,则f(5)=( C )
A.3
B.7
C.11
D.25
[解析] f(5)=2×5+1=11,故选C.
4.(2019·江苏,4)函数y=的定义域是__[-1,7]__.
[解析] 要使函数y=有意义,应满足7+6x-x2≥0,
∴x2-6x-7≤0,∴(x-7)(x+1)≤0,
∴-1≤x≤7,
∴函数y=的定义域是[-1,7].
5.已知f(x)=,g(x)=x2+2.
(1)求f(2),g(2)的值;
(2)求f[g(2)]的值;
(3)求f[g(x)]的解析式.
[解析] (1)f(2)==,g(2)=22+2=6.
(2)f[g(2)]===.
(3)f[g(x)]===.
H
命题方向1 ?函数概念的理解
典例1 (1)下列对应或关系式中是A到B的函数的是( B )
A.A∈R,B∈R,x2+y2=1
B.A={1,2,3,4},B={0,1},对应关系如图:
C.A=R,B=R,f:x→y=
D.A=Z,B=Z,f:x→y=
(2)设M={x|-2≤x≤2},N={y|0≤y≤2},函数y=f(x)的定义域为M,值域为N,对于下列四个图象,不可作为函数y=f(x)的图象的是( C )
[思路分析] (1)如何利用函数定义.对于集合A中的元素通过对应关系在集合B中有唯一元素与之对应进行判断.
(2)当对应关系用图象表示时,怎样判断是否为函数关系.
[解析] (1)对于A项,x2+y2=1可化为y=±,显然对任x∈A,y值不唯一,故不符合.对于B项,符合函数的定义.对于C项,2∈A,但在集合B中找不到与之相对应的数,故不符合.对于D项,-1∈A,但在集合B中找不到与之相对应的数,故不符合.
(2)由函数定义可知,任意作一条直线x=a,则与函数的图象至多有一个交点,结合选项可知C中图象不表示y是x的函数.
『规律方法』 1.判断一个对应关系是否是函数,要从以下三个方面去判断,即A,B必须是非空数集;A中任何一个元素在B中必须有元素与其对应;A中任一元素在B中必有唯一元素与其对应.
2.函数的定义中“任一x”与“有唯一确定的y”说明函数中两变量x,y的对应关系是“一对一”或者是“多对一”而不能是“一对多”.
〔跟踪练习1〕
下列对应是否为A到B的函数:
(1)A=R,B={x|x>0},f:x→y=|x|;
(2)A=Z,B=Z,f:x→y=x2;
(3)A=Z,B=Z,f:x→y=;
(4)A=[-1,1],B={0},f:x→y=0.
[解析] (1)A中的元素0在B中没有对应元素,故不是A到B的函数;
(2)对于集合A中的任意一个整数x,按照对应关系f:x→y=x2,在集合B中都有唯一一个确定的整数x2与之对应,故是集合A到集合B的函数;
(3)A中元素负整数没有平方根,故在B中没有对应的元素,故此对应不是A到B的函数;
(4)对于集合A中一个实数x,按照对应关系f:x→y=0,在集合B中都有唯一一个确定的数0与之对应故是集合A到集合B的函数.
命题方向2 ?求函数的定义域
典例2 求下列函数的定义域:
(1)y=;
(2)f(x)=-.
[思路分析] →→
[解析] (1)要使函数有意义,自变量x的取值必须满足,即,解得x<0,且x≠-2.
故原函数的定义域为(-∞,-2)∪(-2,0).
(2)要使函数有意义,自变量x的取值必须满足,即.
故原函数的定义域为(-∞,1)∪(1,4].
『规律方法』 求函数的定义域:
(1)要明确使各函数表达式有意义的条件是什么,函数有意义的准则一般有:①分式的分母不为0;②偶次根式的被开方数非负;③y=x0要求x≠0.
(2)当一个函数由两个或两个以上代数式的和、差、积、商的形式构成时,定义域是使得各式子都有意义的公共部分的集合.
(3)定义域是一个集合,要用集合或区间表示,若用区间表示数集,不能用“或”连接,而应该用并集符号“∪”连接.
〔跟踪练习2〕
(2019·吉林乾安七中高一期末测试)函数y=的定义域是( C )
A.[-1,+∞)
B.[-1,0]
C.(-1,+∞)
D.(-1,0)
[解析] 要使函数y=有意义,应满足x+1>0,∴x>-1,
∴函数y=的定义域为(-1,+∞).
命题方向3 ?求函数值
典例3 (2019·安徽合肥高一期末测试)已知f(x)=,x∈R.
(1)求f(2),f(),f(3),f()的值;
(2)求f(2)+f(3)+…+f(2
018)+f()+f()+…+f()的值.
[思路分析] (1)将x=2,,3,代入f(x)=计算即可;
(2)由(1)中求得f(2),f(),f(3),f()的值可得f(2)+f()与f(3)+f()的值是定值这一规律,再求得f(2)+f(3)+…+f(2
018)+f()+f()+…+f()的值.
[解析] (1)∵f(x)=,
∴f(2)==,f()==,f(3)==,f()==.
(2)由(1)知,
f(2)+f()=1,f(3)+f()=1.
∴f(a)+f()=+=+·=+=1,
∴f(2)+f(3)+…+f(2
018)+f()+f()+…+f()
=f(2)+f()+f(3)+f()+…+f(2
018)+f()
=2
017.
『规律方法』 解题时要注意审题,观察分析、发现规律.
〔跟踪练习3〕已知函数f(x)=,则f(1)++…+=__-9__.
[解析] ===-1,
∴==…==-1,
又∵f(1)=0,
∴f(1)++…+=-9.
Y 求函数定义域时非等价化简解析式而致误
典例4 求函数y=·的定义域.
[错解] y=·=,由x2-4≥0,得x≥2或x≤-2.∴函数的定义域为{x|x≥2或x≤-2}.
[错因分析] 事实上,函数y=·与y=并不表示同一个函数,求函数定义域应根据原始条件的制约.
[正解] 由,得.即x≥2.∴函数的定义域为{x|x≥2}.
X 求函数值域的方法——转化与化归思想及数形结合思想的应用
1.分离常数法
典例5 求函数y=的值域.
[思路分析] 这种求函数值域的问题,我们常把它们化为y=a+的形式再求函数的值域.
[解析] ∵y===3+,
又∵≠0,∴y≠3.∴函数y=的值域是{y|y∈R,且y≠3}.
『规律方法』 求y=这种类型的函数的值域,应采用分离常数法,将函数化为y=a+的形式.
2.配方法
典例6 求函数y=-x2-2x+3(-5≤x≤-2)的值域.
[思路分析] 这种题型,我们常利用配方法把它们化成y=a(x+b)2+c的形式来求函数的值域.
[解析] ∵y=-x2-2x+3=-(x+1)2+4,x∈[-5,-2],
∴其图象是开口向下,顶点为(-1,4),在x∈[-5,-2]上对应的抛物线上的一段弧.
根据x∈[-5,-2]时的抛物线上升,则当x=-5时,y取最小值,且ymin=-12;当x=-2时,y取最大值,且ymax=3.
故y=-x2-2x+3(-5≤x≤-2)的值域是[-12,3].
『规律方法』 遇到求解一般二次函数y=ax2+bx+c(a≠0)的值域时,应采用配方法,将函数化为y=a(x+)2+的形式,从而求得函数的值域.
3.换元法
典例7 求函数y=x+的值域.
[思路分析] 忽略常数系数,则x与隐含二次关系,若令=t,则x=(t2+1),于是函数转化为以t为自变量的二次函数,由于原函数的定义域由有意义确定,故t的允许取值范围就是的取值范围.
[解析] 设u=(x≥),则x=(u≥0),
于是y=+u=(u≥0).由u≥0知(u+1)2≥1,则y≥.
故函数y=x+的值域为[,+∞).
『规律方法』 求解带根号且被开方式为一次式的函数的值域,直接求解很困难,既费时又费力,所以遇到这样的问题,我们要想到用一个字母代换掉带根号的式子.值得注意的是,在代换过程中,要注意新变量的取值范围.
K
1.下列表格中的x与y能构成函数的是( C )
A.
x
非负数
非正数
y
1
-1
B.
x
奇数
0
偶数
y
1
0
-1
C.
x
有理数
无理数
y
1
-1
D.
x
自然数
整数
有理数
y
1
0
-1
[解析] A中,0既是非负数又是非正数;B中,0又是偶数;D中,自然数也是整数,也是有理数,故选C.
2.(2019·山东莒县一中高一期末测试)下列各组函数中,表示同一函数的是( A )
A.y=x与y=
B.y=x2与y=
C.y=1与y=(x-1)0
D.y=|x|与y=()2
[解析] 选项B、C、D中两函数的定义域不同,只有A中的两函数是同一函数.
3.(2019·江苏苏州市高一期末测试)函数f(x)=的定义域为( D )
A.(1,+∞)
B.[1,+∞)
C.[1,2)
D.[1,2)∪(2,+∞)
[解析] 要使函数有意义,应满足,
∴x≥1且x≠2,故选D.
4.(2019·安徽合肥众兴中学高一期末测试)已知f(x)=2x+3,f(m)=6,则m=____.
[解析] ∵f(x)=2x+3,∴f(m)=2m+3=6,
∴2m=3,∴m=.
5.已知函数f(x)=2x+a,g(x)=(x2+3),若g[f(x)]=x2+x+1,求a的值.
[解析] ∵f(x)=2x+a,g(x)=(x2+3),
∴g[f(x)]=g(2x+a)=[(2x+a)2+3]
=x2+ax+(a2+3).
又∵g[f(x)]=x2+x+1,
∴x2+ax+(a2+3)=x2+x+1,
故a=1.
A级 基础巩固
一、选择题
1.下列四种说法中,不正确的是( B )
A.在函数值域中的每一个数,在定义域中都至少有一个数与之对应
B.函数的定义域和值域一定是无限集合
C.定义域和对应关系确定后,函数的值域也就确定了
D.若函数的定义域中只含有一个元素,则值域也只含有一个元素
[解析] 由函数定义域、值域、对应关系的相关知识,易知选B.
2.已知区间,则实数a满足的条件是( D )
A.a∈R
B.a≤-1
C.a≥-1
D.a>-1
[解析] 由题意得2a+1>a,∴a>-1,故选D.
3.函数y=2x+1,x∈N
,且2≤x≤4,则函数的值域是( C )
A.(5,9)
B.[5,0]
C.{5,7,9}
D.{5,6,7,8,9}
[解析] 由题意,函数的定义域为{2,3,4},当x=2时,y=5;当x=3时,y=7;当x=4时,y=9,所以函数的值域为{5,7,9}.
4.集合A={x|0≤x≤4},B={y|0≤y≤2},下列不表示从A到B的函数是( C )
A.f:x→y=x
B.f:x→y=x
C.f:x→y=x
D.f:
x→y=
[解析] 对于选项C,当x=4时,y=>2不合题意.故选C.
5.函数f(x)对于任意实数x满足f(x+2)=,若f(1)=-5,则f[f(5)]=( C )
A.2
B.5
C.-5
D.-
[解析] ∵f(x+2)=,∴f(x)=,
∴f(1)==-5,∴f(3)=-.
∴f(5)==-5.
6.函数y=f(x)的图象与直线x=m的交点个数为( C )
A.可能有无数个
B.只有一个
C.至多一个
D.至少一个
[解析] 根据函数定义,一个自变量x只能对应一个函数值y,而y=f(x)的定义域中不一定含有m.
二、填空题
7.已知函数f(x)=,又知f(t)=6,则t=__-__.
[解析] f(t)==6.∴t=-.
8.已知f(x)=2x-1,则f[f(2)]=__5__.
[解析] ∵f(x)=2x-1,∴f(2)=2×2-1=3,
∴f[f(2)]=f(3)=2×3-1=5.
三、解答题
9.求下列函数的定义域:
(1)f(x)=;
(2)f(x)=;
(3)f(x)=+.
[解析] (1)要使函数有意义,须使x+2≠0,
∴x≠-2,∴函数f(x)的定义域为{x|x≠-2}.
(2)要使函数有意义,须使3x+2≥0,∴x≥-,
∴函数f(x)的定义域为{x|x≥-}.
(3)要使函数有意义,须使,∴x≥-1且x≠3,∴函数f(x)的定义域为{x|x≥-1且x≠3}.
B级 素养提升
一、选择题
1.设函数f(x)=3x2-1,则f(a)-f(-a)的值是( A )
A.0
B.3a2-1
C.6a2-2
D.6a2
[解析] ∵f(x)=3x2-1,
∴f(a)-f(-a)=3a2-1-[3(-a)2-1]=3a2-1-3a2+1=0.
2.A={x|0≤x≤2},B={y|1≤y≤2},下列图形中能表示以A为定义域,B为值域的函数的是( B )
[解析] A、C、D的值域都不是[1,2],故选B.
3.函数f(x)=的定义域为M,g(x)=的定义域为N,则M∩N=( B )
A.[-1,+∞)
B.[-1,)
C.(-1,)
D.(-∞,)
[解析] ∵M={x|x<},N={x|x≥-1},
∴M∩N={x|-1≤x<}.
故选B.
4.已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:则方程g[f(x)]=x的解集为( C )
x
1
2
3
f(x)
2
3
1
x
1
2
3
g(x)
3
2
1
A.{1}
B.{2}
C.{3}
D.?
[解析] 由题意可知,当x=1时,g[f(1)]=g(2)=2,不满足方程;
当x=2时,g[f(2)]=g(3)=1,不满足方程;
当x=3时,g[f(3)]=g(1)=3,满足方程,故选C.
二、填空题
5.若函数f(x)=ax2-1,a为正常数,且f[f(-1)]=-1,则a的值是__1__.
[解析] f(-1)=a-1,∴f[f(-1)]=f(a-1)=a(a-1)2-1=-1,
∴a(a-1)2=0,
又∵a>0,∴(a-1)2=0,∴a=1.
6.函数y=(1≤x≤3)的值域为__[,8]__.
[解析] ∵1≤x≤3,∴1≤x2≤9,
∴≤≤1,
∴≤≤8,
∴函数y=(1≤x≤3)的值域为[,8].
三、解答题
7.已知函数f(x)=x+.
(1)求f(x)的定义域;
(2)求f(-1),f(2)的值;
(3)当a≠-1时,求f(a+1)的值.
[解析] (1)要使函数有意义,必须使x≠0,
∴f(x)的定义域是(-∞,0)∪(0,+∞).
(2)f(-1)=-1+=-2,f(2)=2+=.
(3)当a≠-1时,a+1≠0,∴f(a+1)=a+1+.
8.已知f(x)=x+1,g(x)=x2,求f[g(x)],g[f(x)].
[解析] ∵f(x)=x+1,g(x)=x2,
∴f[g(x)]=f(x2)
=x2+1.
g[f(x)]=g(x+1)=(x+1)2=x2+2x+1.
9.已知函数f(x)=x2-x+,是否存在实数m,使得该函数在x∈[1,m]时,f(x)的取值范围也是[1,m](m>1)?若存在,求出m的值;若不存在,请说明理由.
[解析] f(x)=x2-x+=(x-1)2+1的图象是一条抛物线,它的对称轴为直线x=1,顶点坐标为(1,1),开口向上,若存在实数m,使该函数在x∈[1,m]时,f(x)的取值范围也是[1,m],则需m>1,且f(m)=m,
即m2-m+=m,即m2-4m+3=0,
解得m=3或m=1(舍去m=1).
故存在实数m=3满足条件.
