1.3探索三角形全等的条件同步练习(带答案)2021-2022学年八年级数学苏科版上册
文档属性
| 名称 | 1.3探索三角形全等的条件同步练习(带答案)2021-2022学年八年级数学苏科版上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 560.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览



文档简介
(江苏省)1.3探索三角形全等的条件(苏科版)八年级数学上册
一、单选题
1.如图,在△ABC中,∠ACB=105°,∠B=30°,∠ACB的平分线CD交AB于点D,则AD:BD=( )
A.
B.
C.1:2
D.
2.如图所示,,,,,,则(
)
A.
B.
C.
D.
3.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是(
)
A.SAS
B.ASA
C.AAS
D.SSS
4.如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN(??
)
A.∠M=∠N
B.AB=CD
C.AM∥CN
D.AM=CN
5.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=
A.40°
B.50°
C.60°
D.75°
7.如图,,,垂足分别为E,F,且,,若,则的度数为(
)
A.
B.
C.
D.
8.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为(
)
A.1
B.2
C.
D.
9.下列条件不能判定两个直角三角形全等的是(
)
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
10.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
11.图中的小正方形边长都相等,若,则点Q可能是图中的(
)
A.点D
B.点C
C.点B
D.点A
12.AD是△BAC的角平分线,过D向AB、AC两边作垂线,垂足为E、F,则下列错误的是( )
A.DE=DF
B.AE=AF
C.BD=CD
D.∠ADE=∠ADF
二、填空题
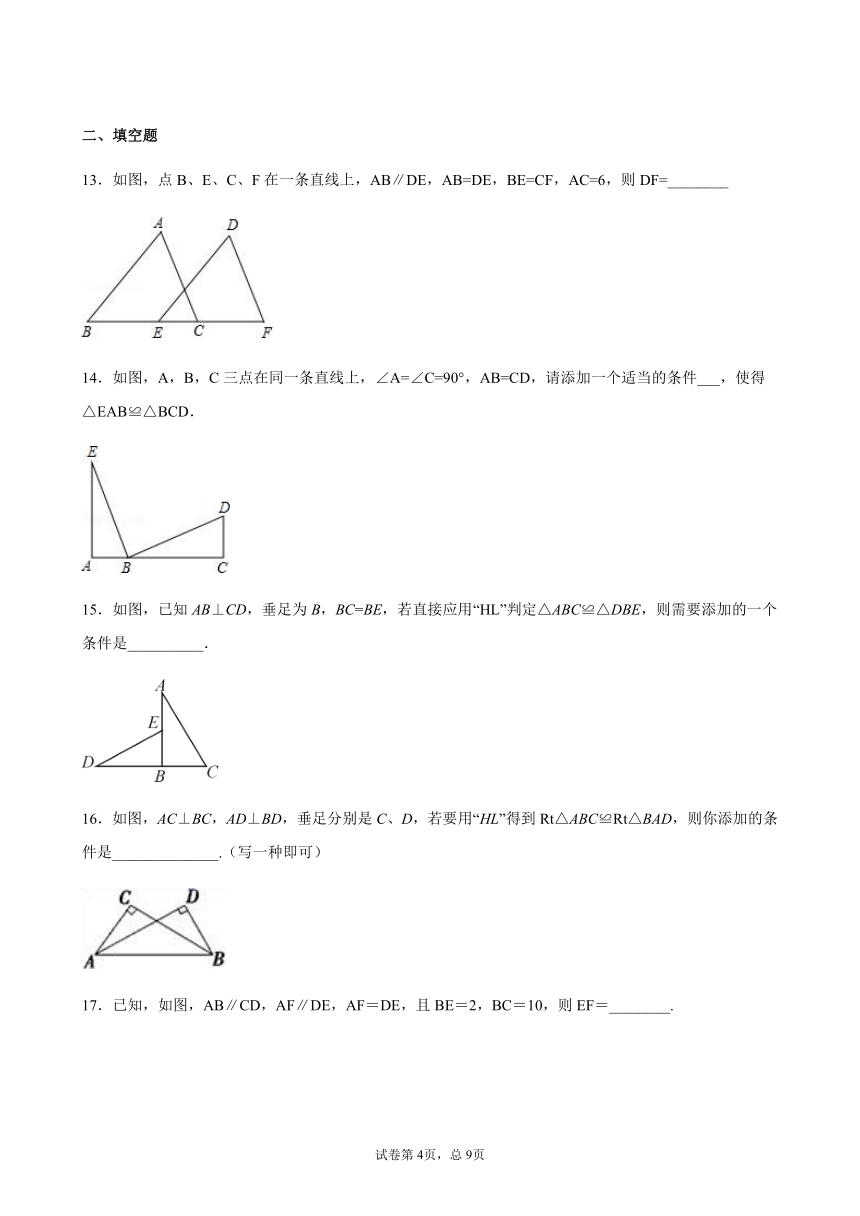
13.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=________
14.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件___,使得△EAB≌△BCD.
15.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是__________.
16.如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是______________.(写一种即可)
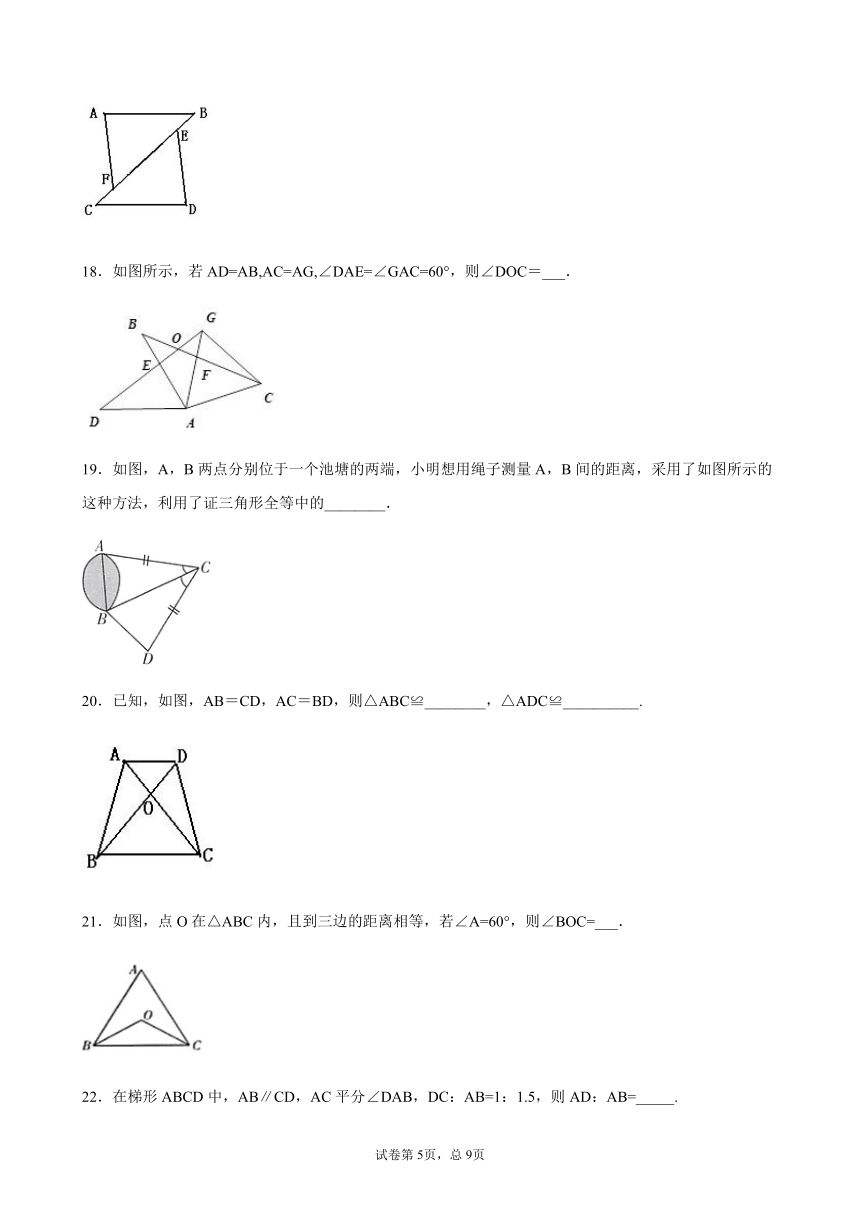
17.已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
18.如图所示,若AD=AB,AC=AG,∠DAE=∠GAC=60°,则∠DOC=___.
19.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,采用了如图所示的这种方法,利用了证三角形全等中的________.
20.已知,如图,AB=CD,AC=BD,则△ABC≌________,△ADC≌__________.
21.如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC=___.
22.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
三、解答题
23.尺规作图:如图,作一个角等于已知角.(要求:写出已知、求作,保留作图痕迹,不写作法).
已知:
求作:
24.如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有几处?请在图中标出来;
25.如图,点E在的外部,点D在BC边上,DE交AC于点F,若,,证明:.
26.如图,点E,F在BC上,,,,求证:.
27.如图,已知ΔABC中,∠ACB=90°,CD⊥AB于D,BF平分∠ABC交CD于E,交AC于F.
求证:CE=CF.
28.如图,已知:,,AE是的中线,求证:.
29.证明“全等三角形的对应角平分线相等”,命题证明应有四个步骤:画出图形,写出已知,求证及证明过程,把下列证明补完整.
图形:如图所示:
已知:
求证:
证明:
30.在中,,F为AB延长线上一点,点E在BC上,且.
(1)求证:
(2)若,求度数.
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.A
【解析】因为角平分线上的点到角两边的距离相等,作DE垂直BC,DF垂直AC,设DE=DF=a,则AD=,BD=2a,所以AD:BD=.故选择A.
2.C
【解析】,
,
即.
,
.
,
,
.
,,
,
.
故选C.
3.A
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
4.D
【解析】A、在△ABM和△CDN
中,
∠M=∠N
,MB=ND,∠MBA=∠NDC,
△ABM≌△CDN
(ASA),
则A正确;
B、在△ABM和△CDN
中,
MB=ND,∠MBA=∠NDC,AB=CD,
△ABM≌△CDN
(SAS),
则B正确;
C、AM∥CN,得∠A=∠C,
在△ABM和△CDN
中,
∠A=∠C,∠MBA=∠NDC,MB=ND,
△ABM≌△CDN
(AAS),
则C正确;
D、AM=CN,MB=ND,∠MBA=∠NDC≠90?,
则D不正确.
故选择:D.
5.A
【解析】解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
6.B
【解析】解:∵∠B=∠D=90°
在Rt△ABC和Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠2=∠ACB=90°-∠1=50°.
故选B.
7.C
【解析】,
∴,
即.
又,,
和均为直角三角形.
在和中,
,
∴,
.
,
,
.
故选C.
8.B
【解析】∵AD⊥BC,CE⊥AB,
∴∠BEC=∠ADB=90°,
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BAD=∠BCE,
在△BCE和△HAE中,
,
∴△BCE≌△HAE(AAS),
∴CE=AE=6,
∴CH=CE-HE=6-4=2.
故选:B.
9.D
【解析】解:、可以利用边角边判定两三角形全等,故本选项不合题意;
、可以利用角角边判定两三角形全等,故本选项不合题意;
、根据斜边直角边定理判定两三角形全等,故本选项不合题意;
、三个角对应相等不能证明两三角形全等,故本选项符合题意;
故选:D.
10.D
【解析】∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
11.A
【解析】解:观察图象可知△MNP≌△MFD.
故选:A.
12.C
【解析】解:如图,∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,故A选项错误,
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,故B、D选项错误,
只有△ABC是等腰三角形时,BD=CD,故C选项正确.
故选C.
13.6.
【解析】∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
14.AE=CB(答案不唯一)
【解析】∵∠A=∠C=90°,AB=CD,
∴若添加AE=CB可由“SAS”证得△EAB≌△BCD,
若添加EB=BD可由“HL”
证得△EAB≌△BCD,
若添加∠EBD=90°可由“ASA”或“AAB”
证得△EAB≌△BCD,
若添加∠E=∠DBC,可由“ASA”“AAS”证得△EAB≌△BCD.
等,答案不唯一.
15.AC=DE
【解析】用“HL”判定△ABC≌△DBE,已知BC=BE,再添加斜边DE=AC即可.
16.AC=BD或AD=BC.(答案不唯一)
【解析】AC=BD或AD=BC都可以.
17.6
【解析】∵AB∥CD,AF∥DE,
∴∠B=∠C,∠AFB=∠DEC,
在△ABF和△CDE中
,
∴△ABF≌△DCE(AAS),
∴BF=CE,
∴BF?EF=CE?EF,
即CF=EB=2,
∵BC=10,
∴EF=10?2?2=6,
故答案为6.
18.120°
【解析】解:
在与中,
故答案为:
19.SAS
【解析】观察图形发现:,,,
所以利用了证三角形全等中的SAS(或边角边).
故答案为:SAS.
20.△DCB,
△DAB.
【解析】∵AB=CD,AC=BD,BC=CB,
∴△ABC≌△DCB(SSS),
∵AB=CD,AC=BD,AD=AD,
∴△ADC≌△DAB.
21.120°
【解析】∵点O在△ABC内,且到三边的距离相等,
∴点O是三个角的平分线的交点,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=(180°-60°)=60°,
在△BCO中,∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
故答案为120°.
22.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD
=∠DCA
∴AD
=
CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
23.见解析.
【解析】已知:∠AOB,
求作:∠ECF等于∠AOB,
如图所示:
∠ECF即为所求
24.可供选择的地址有4处,图见解析
【解析】满足条件的有:(1)三角形两个内角平分线的交点,共一处;(2)三个外角两两平分线的交点,共三处.
∴可供选择的地址有4处(如图所示).
25.证明见解析.
【解析】证明:,,
,
,
,
在与中,
,
.
26.详见解析
【解析】,
,即,
在与中,
,
.
27.详见解析.
【解析】证明:∵∠ACB=90°,CD⊥AB
∴∠CBF+∠CFB=∠DBE+∠DEB=90°
∵BF平分∠ABC
∴∠CBF=∠DBE
∴∠CFB=∠DEB
∵∠FEC=∠DEB
∴∠CFB=∠FEC
∴CE=CF
28.见解析
【解析】延长AE至F,使EF
=AE,连接BF.
在与中,
,
,
,,
,,
.
在与中,
,
,
.
,
.
29.见详解
【解析】解:已知:如图,,、分别是和的角平分线.
求证:.
证明:∵
∴,,
∵、分别是和的角平分线
∴,
∴
在和中
∴
∴.
30.(1)见解析;(2).
【解析】(1)∵∠ABC=90°,
∴∠CBF=∠ABC=90°,
在和中,
∴(HL);
(2)∵,
∴,
∴
答案第1页,总2页
答案第1页,总2页
一、单选题
1.如图,在△ABC中,∠ACB=105°,∠B=30°,∠ACB的平分线CD交AB于点D,则AD:BD=( )
A.
B.
C.1:2
D.
2.如图所示,,,,,,则(
)
A.
B.
C.
D.
3.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是(
)
A.SAS
B.ASA
C.AAS
D.SSS
4.如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN(??
)
A.∠M=∠N
B.AB=CD
C.AM∥CN
D.AM=CN
5.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=
A.40°
B.50°
C.60°
D.75°
7.如图,,,垂足分别为E,F,且,,若,则的度数为(
)
A.
B.
C.
D.
8.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为(
)
A.1
B.2
C.
D.
9.下列条件不能判定两个直角三角形全等的是(
)
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
10.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
11.图中的小正方形边长都相等,若,则点Q可能是图中的(
)
A.点D
B.点C
C.点B
D.点A
12.AD是△BAC的角平分线,过D向AB、AC两边作垂线,垂足为E、F,则下列错误的是( )
A.DE=DF
B.AE=AF
C.BD=CD
D.∠ADE=∠ADF
二、填空题
13.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=________
14.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件___,使得△EAB≌△BCD.
15.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是__________.
16.如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是______________.(写一种即可)
17.已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
18.如图所示,若AD=AB,AC=AG,∠DAE=∠GAC=60°,则∠DOC=___.
19.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,采用了如图所示的这种方法,利用了证三角形全等中的________.
20.已知,如图,AB=CD,AC=BD,则△ABC≌________,△ADC≌__________.
21.如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC=___.
22.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
三、解答题
23.尺规作图:如图,作一个角等于已知角.(要求:写出已知、求作,保留作图痕迹,不写作法).
已知:
求作:
24.如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有几处?请在图中标出来;
25.如图,点E在的外部,点D在BC边上,DE交AC于点F,若,,证明:.
26.如图,点E,F在BC上,,,,求证:.
27.如图,已知ΔABC中,∠ACB=90°,CD⊥AB于D,BF平分∠ABC交CD于E,交AC于F.
求证:CE=CF.
28.如图,已知:,,AE是的中线,求证:.
29.证明“全等三角形的对应角平分线相等”,命题证明应有四个步骤:画出图形,写出已知,求证及证明过程,把下列证明补完整.
图形:如图所示:
已知:
求证:
证明:
30.在中,,F为AB延长线上一点,点E在BC上,且.
(1)求证:
(2)若,求度数.
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.A
【解析】因为角平分线上的点到角两边的距离相等,作DE垂直BC,DF垂直AC,设DE=DF=a,则AD=,BD=2a,所以AD:BD=.故选择A.
2.C
【解析】,
,
即.
,
.
,
,
.
,,
,
.
故选C.
3.A
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
4.D
【解析】A、在△ABM和△CDN
中,
∠M=∠N
,MB=ND,∠MBA=∠NDC,
△ABM≌△CDN
(ASA),
则A正确;
B、在△ABM和△CDN
中,
MB=ND,∠MBA=∠NDC,AB=CD,
△ABM≌△CDN
(SAS),
则B正确;
C、AM∥CN,得∠A=∠C,
在△ABM和△CDN
中,
∠A=∠C,∠MBA=∠NDC,MB=ND,
△ABM≌△CDN
(AAS),
则C正确;
D、AM=CN,MB=ND,∠MBA=∠NDC≠90?,
则D不正确.
故选择:D.
5.A
【解析】解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
6.B
【解析】解:∵∠B=∠D=90°
在Rt△ABC和Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠2=∠ACB=90°-∠1=50°.
故选B.
7.C
【解析】,
∴,
即.
又,,
和均为直角三角形.
在和中,
,
∴,
.
,
,
.
故选C.
8.B
【解析】∵AD⊥BC,CE⊥AB,
∴∠BEC=∠ADB=90°,
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BAD=∠BCE,
在△BCE和△HAE中,
,
∴△BCE≌△HAE(AAS),
∴CE=AE=6,
∴CH=CE-HE=6-4=2.
故选:B.
9.D
【解析】解:、可以利用边角边判定两三角形全等,故本选项不合题意;
、可以利用角角边判定两三角形全等,故本选项不合题意;
、根据斜边直角边定理判定两三角形全等,故本选项不合题意;
、三个角对应相等不能证明两三角形全等,故本选项符合题意;
故选:D.
10.D
【解析】∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
11.A
【解析】解:观察图象可知△MNP≌△MFD.
故选:A.
12.C
【解析】解:如图,∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,故A选项错误,
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,故B、D选项错误,
只有△ABC是等腰三角形时,BD=CD,故C选项正确.
故选C.
13.6.
【解析】∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
14.AE=CB(答案不唯一)
【解析】∵∠A=∠C=90°,AB=CD,
∴若添加AE=CB可由“SAS”证得△EAB≌△BCD,
若添加EB=BD可由“HL”
证得△EAB≌△BCD,
若添加∠EBD=90°可由“ASA”或“AAB”
证得△EAB≌△BCD,
若添加∠E=∠DBC,可由“ASA”“AAS”证得△EAB≌△BCD.
等,答案不唯一.
15.AC=DE
【解析】用“HL”判定△ABC≌△DBE,已知BC=BE,再添加斜边DE=AC即可.
16.AC=BD或AD=BC.(答案不唯一)
【解析】AC=BD或AD=BC都可以.
17.6
【解析】∵AB∥CD,AF∥DE,
∴∠B=∠C,∠AFB=∠DEC,
在△ABF和△CDE中
,
∴△ABF≌△DCE(AAS),
∴BF=CE,
∴BF?EF=CE?EF,
即CF=EB=2,
∵BC=10,
∴EF=10?2?2=6,
故答案为6.
18.120°
【解析】解:
在与中,
故答案为:
19.SAS
【解析】观察图形发现:,,,
所以利用了证三角形全等中的SAS(或边角边).
故答案为:SAS.
20.△DCB,
△DAB.
【解析】∵AB=CD,AC=BD,BC=CB,
∴△ABC≌△DCB(SSS),
∵AB=CD,AC=BD,AD=AD,
∴△ADC≌△DAB.
21.120°
【解析】∵点O在△ABC内,且到三边的距离相等,
∴点O是三个角的平分线的交点,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=(180°-60°)=60°,
在△BCO中,∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
故答案为120°.
22.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD
=∠DCA
∴AD
=
CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
23.见解析.
【解析】已知:∠AOB,
求作:∠ECF等于∠AOB,
如图所示:
∠ECF即为所求
24.可供选择的地址有4处,图见解析
【解析】满足条件的有:(1)三角形两个内角平分线的交点,共一处;(2)三个外角两两平分线的交点,共三处.
∴可供选择的地址有4处(如图所示).
25.证明见解析.
【解析】证明:,,
,
,
,
在与中,
,
.
26.详见解析
【解析】,
,即,
在与中,
,
.
27.详见解析.
【解析】证明:∵∠ACB=90°,CD⊥AB
∴∠CBF+∠CFB=∠DBE+∠DEB=90°
∵BF平分∠ABC
∴∠CBF=∠DBE
∴∠CFB=∠DEB
∵∠FEC=∠DEB
∴∠CFB=∠FEC
∴CE=CF
28.见解析
【解析】延长AE至F,使EF
=AE,连接BF.
在与中,
,
,
,,
,,
.
在与中,
,
,
.
,
.
29.见详解
【解析】解:已知:如图,,、分别是和的角平分线.
求证:.
证明:∵
∴,,
∵、分别是和的角平分线
∴,
∴
在和中
∴
∴.
30.(1)见解析;(2).
【解析】(1)∵∠ABC=90°,
∴∠CBF=∠ABC=90°,
在和中,
∴(HL);
(2)∵,
∴,
∴
答案第1页,总2页
答案第1页,总2页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
