第5章相交线与平行线 单元自我综合评价 2021-2022学年华东师大版数学七年级上册(word版含答案)
文档属性
| 名称 | 第5章相交线与平行线 单元自我综合评价 2021-2022学年华东师大版数学七年级上册(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 224.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览



文档简介
第5章 相交线与平行线自我综合评价
一、选择题(每小题4分,共32分)
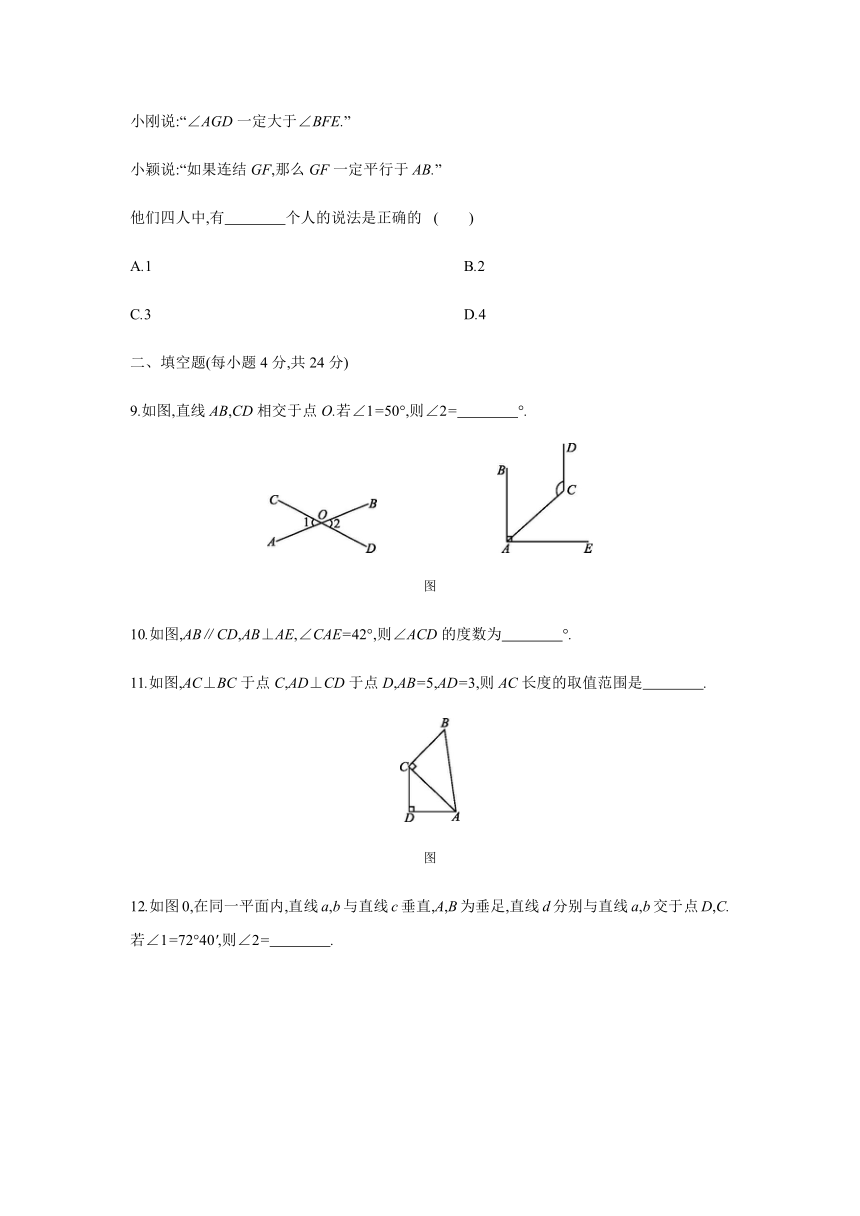
1.如图,某地进行城市规划,在一条新修公路旁有一超市,现要建一个汽车站.为了使超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )
A.点A
B.点B
C.点C
D.点D
2.如图所示,下列说法错误的是
( )
A.∠A和∠3是同位角
B.∠2和∠3是同旁内角
C.∠A和∠B是同旁内角
D.∠C和∠1是内错角
3.如图,AB⊥AC,AD⊥BC,能表示点到直线(或线段)的距离的线段有
( )
A.3条
B.4条
C.5条
D.6条
4.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是
( )
A.154°
B.144°
C.134°
D.124°
5.一辆汽车在笔直的公路上行驶,第一次左拐50°,再在笔直的公路上行驶一段距离后,第二次右拐50°,两次拐弯后的行驶方向与原来的行驶方向
( )
A.恰好相同
B.恰好相反
C.互相垂直
D.夹角为100°
6.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=40°时,∠BOD的度数是( )
A.50°
B.130°
C.50°或90°
D.50°或130°
7.如图所示,AD⊥BC于点D,DE∥BA交边AC于点E,则∠α与∠β的关系是
( )
A.互余
B.互补
C.相等
D.以上都不对
8.小明、小亮、小刚、小颖一起研究一道数学题.
如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有 个人的说法是正确的
( )?
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
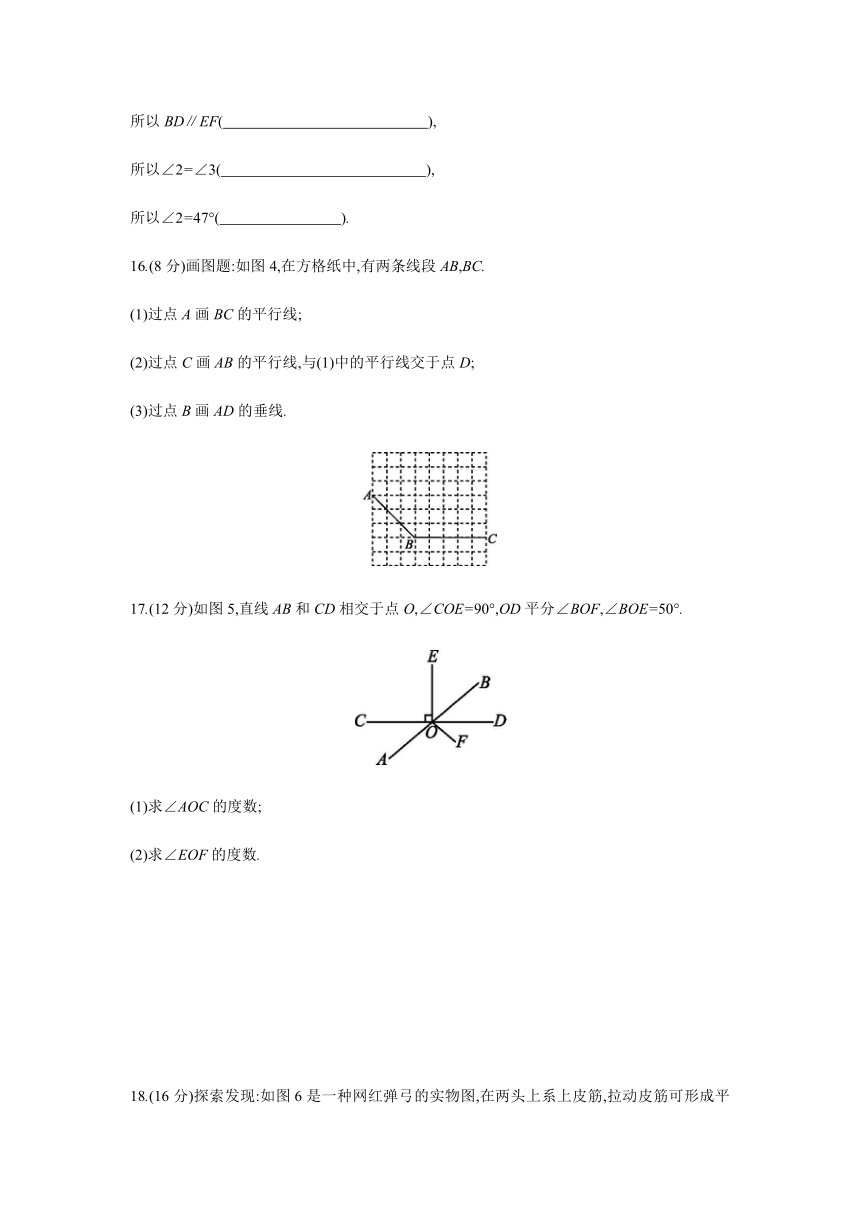
9.如图,直线AB,CD相交于点O.若∠1=50°,则∠2= °.?
图
10.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 °.?
11.如图,AC⊥BC于点C,AD⊥CD于点D,AB=5,AD=3,则AC长度的取值范围是 .?
图
12.如图0,在同一平面内,直线a,b与直线c垂直,A,B为垂足,直线d分别与直线a,b交于点D,C.若∠1=72°40',则∠2= .?
13.如图1,已知直线a∥b,用一块含30°角的三角尺按图中所示的方式放置,若∠1=25°,则∠2= °.?
图1
14.如图2,已知AB∥CD,点E,F分别在直线AB,CD上,点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线互相垂直,则∠EPF的度数为 .?
三、解答题(共44分)
15.(8分)如图3,AD∥BC,BD⊥CD,EF⊥CD,垂足分别是D,F,∠1=47°,求∠2的度数.
完成下列推理过程:
解:因为AD∥BC(已知),
所以∠1= ( ).?
因为∠1=47°,
所以 =47°( ).?
因为BD⊥CD,EF⊥CD,
所以∠BDC=∠EFC=90°,
所以BD∥EF(
),?
所以∠2=∠3(
),?
所以∠2=47°( ).?
16.(8分)画图题:如图4,在方格纸中,有两条线段AB,BC.
(1)过点A画BC的平行线;
(2)过点C画AB的平行线,与(1)中的平行线交于点D;
(3)过点B画AD的垂线.
17.(12分)如图5,直线AB和CD相交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
18.(16分)探索发现:如图6是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图(图7①),弹弓的两边可看成是平行的,即AB∥CD.各活动小组探索∠APC与∠A,∠C之间的数量关系.已知AB∥CD,点P不在直线AB和直线CD上,在图①中,智慧小组发现:∠APC=∠A+∠C.
智慧小组是这样思考的:过点P作PQ∥AB……
请你按照智慧小组作的辅助线补全推理过程.
类比思考:(1)在图②中,∠APC与∠A,∠C之间的数量关系为 ;?
(2)如图③,已知AB∥CD,则∠α,∠β,∠γ之间的数量关系为 .?
解决问题:善思小组提出:如图7④⑤,AB∥CD,AF,CF分别平分∠BAP,∠DCP.
(1)在图④中,∠AFC与∠APC之间的数量关系为 ;?
(2)在图⑤中,∠AFC与∠APC之间的数量关系为 .?
答案
1.C
2.B
3.C [解析]
线段AB的长是点B到AC的距离,
线段CA的长是点C到AB的距离,
线段AD的长是点A到BC的距离,
线段BD的长是点B到AD的距离,
线段CD的长是点C到AD的距离,
故图中能表示点到直线(或线段)的距离的线段共有5条.
故选C.
4.D [解析]
∵DA⊥AB,CD⊥DA,
∴AB∥CD,
∴∠B+∠C=180°.
∵∠B=56°,
∴∠C=180°-∠B=124°.
故选D.
5.A [解析]
如图所示(实线为行驶路线),
符合“同位角相等,两直线平行”的判定,
所以两次拐弯后的行驶方向与原来的行驶方向恰好相同.
故选A.
6.D 7.A 8.B 9.50
10.132 [解析]
∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°-42°=48°.
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故答案为:132.
11.3因为AC⊥BC于点C,AB=5,
所以AC因为AD⊥CD于点D,AD=3,
所以AC>AD=3,所以3故答案为312.107°20'
13.35 [解析]
如图,过点B作EF∥a.
∵a∥b,∴EF∥a∥b.
∴∠1=∠ABF,∠2=∠CBF.
∵△ABC是含30°角的直角三角形,
∴∠ABC=60°.
∵∠ABF+∠CBF=60°,
∴∠2=60°-25°=35°.
故答案为:35.
14.45°或135° [解析]
如图①,过点M作MN∥AB.
∵AB∥CD,∴AB∥CD∥MN,
∴∠AEM=∠EMN,∠NMF=∠MFC.
∵∠EMF=90°,∴∠AEM+∠CFM=90°.
同理可得∠P=∠AEP+∠CFP.
由折叠可得:∠AEP=∠PEM=∠AEM,∠PFC=∠PFM=∠MFC,
∴∠P=(∠AEM+∠CFM)=45°.
如图②,过点M作MN∥AB.
∵AB∥CD,
∴AB∥CD∥MN,
∴∠AEM+∠EMN=180°,∠NMF+∠CFM=180°,
∴∠AEM+∠EMF+∠CFM=360°.
∵∠EMF=90°,
∴∠AEM+∠CFM=360°-90°=270°.
由折叠可得:∠AEP=∠PEM=∠AEM,∠PFC=∠PFM=∠CFM,
∴∠P=270°×=135°.
综上所述:∠EPF的度数为45°或135°.
故答案为:45°或135°.
15.∠3 两直线平行,内错角相等
∠3 等量代换 同位角相等,两直线平行
两直线平行,同位角相等 等量代换
16.略
17.解:(1)因为∠BOE=50°,∠COE=90°,
∠AOC+∠COE+∠BOE=180°,
所以∠AOC=180°-50°-90°=40°.
(2)因为∠DOE=∠COE=90°,
所以∠BOD=90°-50°=40°.
因为OD平分∠BOF,
所以∠DOF=∠BOD=40°,
所以∠EOF=50°+40°+40°=130°.
18.解:探索发现:所以∠APQ=∠A.
因为PQ∥AB,AB∥CD,
所以PQ∥CD,
所以∠CPQ=∠C,
所以∠APQ+∠CPQ=∠A+∠C,
所以∠APC=∠A+∠C.
类比思考:(1)∠APC+∠A+∠C=360°.
理由如下:
过点P作PQ∥AB,如图(a)所示,
所以∠APQ+∠A=180°.
因为PQ∥AB,AB∥CD,
所以PQ∥CD,所以∠CPQ+∠C=180°,
所以∠APQ+∠CPQ+∠A+∠C=180°+180°=360°.
又因为∠APC=∠APQ+∠CPQ,
所以∠APC+∠A+∠C=360°.
(2)∠α+∠β-∠γ=180°.理由如下:
过点M作MQ∥AB,如图(b)所示,
所以∠α+∠QMA=180°.
因为MQ∥AB,AB∥CD,
所以MQ∥CD,所以∠QMD=∠γ.
因为∠QMA+∠QMD=∠β,
所以∠α+∠β-∠γ=180°.
解决问题:(1)∠AFC=∠APC.理由如下:
过点P作PQ∥AB,过点F作FM∥AB,如图(c)所示,
所以∠APQ=∠BAP,∠AFM=∠BAF.
因为AF平分∠BAP,
所以∠BAF=∠BAP,
所以∠AFM=∠BAP.
因为PQ∥AB,FM∥AB,AB∥CD,
所以PQ∥CD,FM∥CD,
所以∠CPQ=∠DCP,∠CFM=∠DCF.
所以∠APC=∠BAP+∠DCP.
因为CF平分∠DCP,
所以∠DCF=∠DCP,
所以∠CFM=∠DCP,
所以∠AFC=∠BAP+∠DCP=(∠BAP+∠DCP)=∠APC,
即∠AFC=∠APC.
(2)∠AFC=180°-∠APC.理由如下:
由“探索发现”可得∠AFC=∠FAB+∠FCD.
由“类比思考”(1)可得∠APC=360°-∠PAB-∠PCD=360°-2(∠FAB+∠FCD)=360°-2∠AFC,
所以∠AFC=(360°-∠APC)=180°-∠APC.
一、选择题(每小题4分,共32分)
1.如图,某地进行城市规划,在一条新修公路旁有一超市,现要建一个汽车站.为了使超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )
A.点A
B.点B
C.点C
D.点D
2.如图所示,下列说法错误的是
( )
A.∠A和∠3是同位角
B.∠2和∠3是同旁内角
C.∠A和∠B是同旁内角
D.∠C和∠1是内错角
3.如图,AB⊥AC,AD⊥BC,能表示点到直线(或线段)的距离的线段有
( )
A.3条
B.4条
C.5条
D.6条
4.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是
( )
A.154°
B.144°
C.134°
D.124°
5.一辆汽车在笔直的公路上行驶,第一次左拐50°,再在笔直的公路上行驶一段距离后,第二次右拐50°,两次拐弯后的行驶方向与原来的行驶方向
( )
A.恰好相同
B.恰好相反
C.互相垂直
D.夹角为100°
6.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=40°时,∠BOD的度数是( )
A.50°
B.130°
C.50°或90°
D.50°或130°
7.如图所示,AD⊥BC于点D,DE∥BA交边AC于点E,则∠α与∠β的关系是
( )
A.互余
B.互补
C.相等
D.以上都不对
8.小明、小亮、小刚、小颖一起研究一道数学题.
如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有 个人的说法是正确的
( )?
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
9.如图,直线AB,CD相交于点O.若∠1=50°,则∠2= °.?
图
10.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 °.?
11.如图,AC⊥BC于点C,AD⊥CD于点D,AB=5,AD=3,则AC长度的取值范围是 .?
图
12.如图0,在同一平面内,直线a,b与直线c垂直,A,B为垂足,直线d分别与直线a,b交于点D,C.若∠1=72°40',则∠2= .?
13.如图1,已知直线a∥b,用一块含30°角的三角尺按图中所示的方式放置,若∠1=25°,则∠2= °.?
图1
14.如图2,已知AB∥CD,点E,F分别在直线AB,CD上,点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线互相垂直,则∠EPF的度数为 .?
三、解答题(共44分)
15.(8分)如图3,AD∥BC,BD⊥CD,EF⊥CD,垂足分别是D,F,∠1=47°,求∠2的度数.
完成下列推理过程:
解:因为AD∥BC(已知),
所以∠1= ( ).?
因为∠1=47°,
所以 =47°( ).?
因为BD⊥CD,EF⊥CD,
所以∠BDC=∠EFC=90°,
所以BD∥EF(
),?
所以∠2=∠3(
),?
所以∠2=47°( ).?
16.(8分)画图题:如图4,在方格纸中,有两条线段AB,BC.
(1)过点A画BC的平行线;
(2)过点C画AB的平行线,与(1)中的平行线交于点D;
(3)过点B画AD的垂线.
17.(12分)如图5,直线AB和CD相交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
18.(16分)探索发现:如图6是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图(图7①),弹弓的两边可看成是平行的,即AB∥CD.各活动小组探索∠APC与∠A,∠C之间的数量关系.已知AB∥CD,点P不在直线AB和直线CD上,在图①中,智慧小组发现:∠APC=∠A+∠C.
智慧小组是这样思考的:过点P作PQ∥AB……
请你按照智慧小组作的辅助线补全推理过程.
类比思考:(1)在图②中,∠APC与∠A,∠C之间的数量关系为 ;?
(2)如图③,已知AB∥CD,则∠α,∠β,∠γ之间的数量关系为 .?
解决问题:善思小组提出:如图7④⑤,AB∥CD,AF,CF分别平分∠BAP,∠DCP.
(1)在图④中,∠AFC与∠APC之间的数量关系为 ;?
(2)在图⑤中,∠AFC与∠APC之间的数量关系为 .?
答案
1.C
2.B
3.C [解析]
线段AB的长是点B到AC的距离,
线段CA的长是点C到AB的距离,
线段AD的长是点A到BC的距离,
线段BD的长是点B到AD的距离,
线段CD的长是点C到AD的距离,
故图中能表示点到直线(或线段)的距离的线段共有5条.
故选C.
4.D [解析]
∵DA⊥AB,CD⊥DA,
∴AB∥CD,
∴∠B+∠C=180°.
∵∠B=56°,
∴∠C=180°-∠B=124°.
故选D.
5.A [解析]
如图所示(实线为行驶路线),
符合“同位角相等,两直线平行”的判定,
所以两次拐弯后的行驶方向与原来的行驶方向恰好相同.
故选A.
6.D 7.A 8.B 9.50
10.132 [解析]
∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°-42°=48°.
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故答案为:132.
11.3
所以AC
所以AC>AD=3,所以3
13.35 [解析]
如图,过点B作EF∥a.
∵a∥b,∴EF∥a∥b.
∴∠1=∠ABF,∠2=∠CBF.
∵△ABC是含30°角的直角三角形,
∴∠ABC=60°.
∵∠ABF+∠CBF=60°,
∴∠2=60°-25°=35°.
故答案为:35.
14.45°或135° [解析]
如图①,过点M作MN∥AB.
∵AB∥CD,∴AB∥CD∥MN,
∴∠AEM=∠EMN,∠NMF=∠MFC.
∵∠EMF=90°,∴∠AEM+∠CFM=90°.
同理可得∠P=∠AEP+∠CFP.
由折叠可得:∠AEP=∠PEM=∠AEM,∠PFC=∠PFM=∠MFC,
∴∠P=(∠AEM+∠CFM)=45°.
如图②,过点M作MN∥AB.
∵AB∥CD,
∴AB∥CD∥MN,
∴∠AEM+∠EMN=180°,∠NMF+∠CFM=180°,
∴∠AEM+∠EMF+∠CFM=360°.
∵∠EMF=90°,
∴∠AEM+∠CFM=360°-90°=270°.
由折叠可得:∠AEP=∠PEM=∠AEM,∠PFC=∠PFM=∠CFM,
∴∠P=270°×=135°.
综上所述:∠EPF的度数为45°或135°.
故答案为:45°或135°.
15.∠3 两直线平行,内错角相等
∠3 等量代换 同位角相等,两直线平行
两直线平行,同位角相等 等量代换
16.略
17.解:(1)因为∠BOE=50°,∠COE=90°,
∠AOC+∠COE+∠BOE=180°,
所以∠AOC=180°-50°-90°=40°.
(2)因为∠DOE=∠COE=90°,
所以∠BOD=90°-50°=40°.
因为OD平分∠BOF,
所以∠DOF=∠BOD=40°,
所以∠EOF=50°+40°+40°=130°.
18.解:探索发现:所以∠APQ=∠A.
因为PQ∥AB,AB∥CD,
所以PQ∥CD,
所以∠CPQ=∠C,
所以∠APQ+∠CPQ=∠A+∠C,
所以∠APC=∠A+∠C.
类比思考:(1)∠APC+∠A+∠C=360°.
理由如下:
过点P作PQ∥AB,如图(a)所示,
所以∠APQ+∠A=180°.
因为PQ∥AB,AB∥CD,
所以PQ∥CD,所以∠CPQ+∠C=180°,
所以∠APQ+∠CPQ+∠A+∠C=180°+180°=360°.
又因为∠APC=∠APQ+∠CPQ,
所以∠APC+∠A+∠C=360°.
(2)∠α+∠β-∠γ=180°.理由如下:
过点M作MQ∥AB,如图(b)所示,
所以∠α+∠QMA=180°.
因为MQ∥AB,AB∥CD,
所以MQ∥CD,所以∠QMD=∠γ.
因为∠QMA+∠QMD=∠β,
所以∠α+∠β-∠γ=180°.
解决问题:(1)∠AFC=∠APC.理由如下:
过点P作PQ∥AB,过点F作FM∥AB,如图(c)所示,
所以∠APQ=∠BAP,∠AFM=∠BAF.
因为AF平分∠BAP,
所以∠BAF=∠BAP,
所以∠AFM=∠BAP.
因为PQ∥AB,FM∥AB,AB∥CD,
所以PQ∥CD,FM∥CD,
所以∠CPQ=∠DCP,∠CFM=∠DCF.
所以∠APC=∠BAP+∠DCP.
因为CF平分∠DCP,
所以∠DCF=∠DCP,
所以∠CFM=∠DCP,
所以∠AFC=∠BAP+∠DCP=(∠BAP+∠DCP)=∠APC,
即∠AFC=∠APC.
(2)∠AFC=180°-∠APC.理由如下:
由“探索发现”可得∠AFC=∠FAB+∠FCD.
由“类比思考”(1)可得∠APC=360°-∠PAB-∠PCD=360°-2(∠FAB+∠FCD)=360°-2∠AFC,
所以∠AFC=(360°-∠APC)=180°-∠APC.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
