1.2.2直角三角形斜边上的中线同步练习2021——2022学年北师大版九年级数学上册(word版含解析)
文档属性
| 名称 | 1.2.2直角三角形斜边上的中线同步练习2021——2022学年北师大版九年级数学上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 06:04:25 | ||
图片预览


文档简介
1.2.2直角三角形斜边上的中线
一.选择题(共7小题)
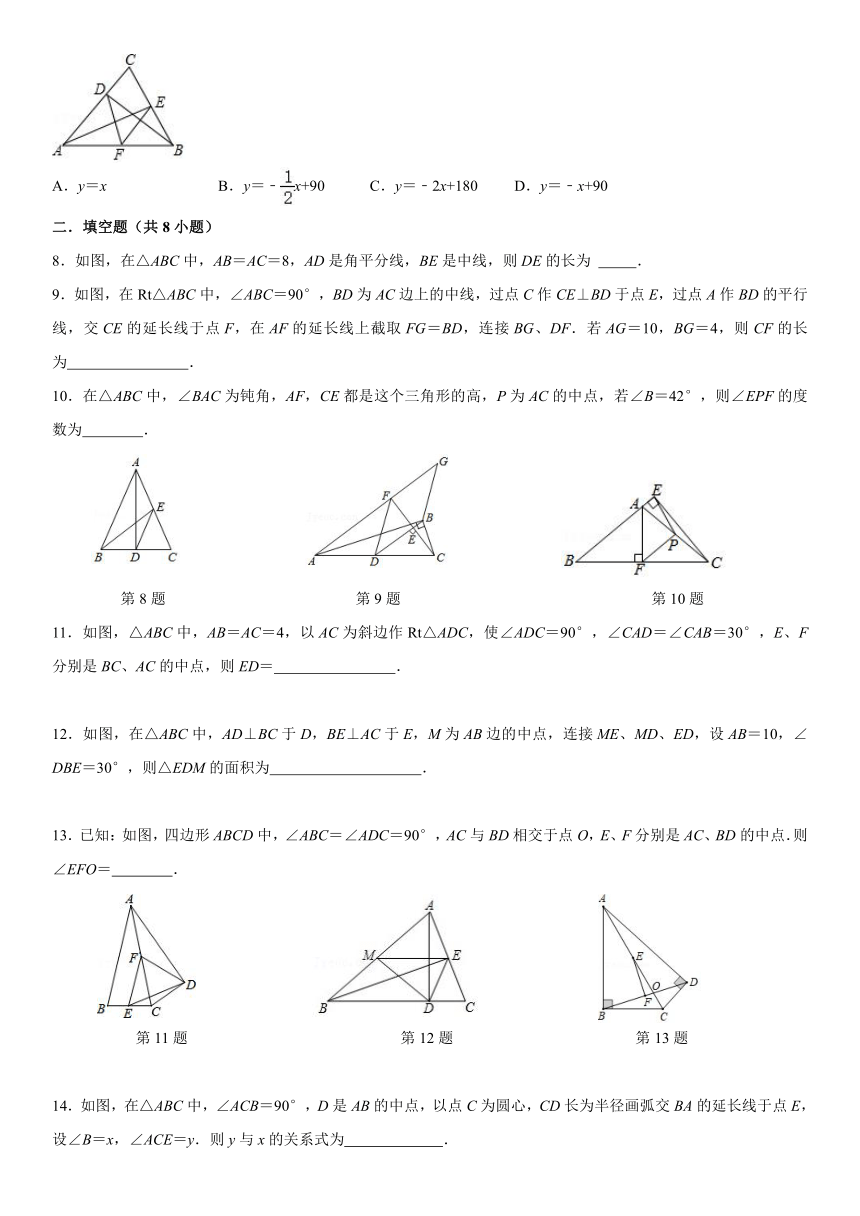
1.如图所示,公路AC,BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为5km,则M,C两点间的距离为( )
A.2.5km
B.3km
C.4.5km
D.5km
2.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为( )
A.3
B.4
C.5
D.6
3.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=( )
A.2
B.3
C.4
D.6
第1题
第2题
第3题
4.如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
5.如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19°
B.33°
C.34°
D.43°
6.如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )
A.2
B.
C.8
D.9
第4题
第5题
第6题
7.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D;点F是AB的中点,连接DF,EF,设∠DFE=x°,∠ACB=y°,则( )
A.y=x
B.y=﹣x+90
C.y=﹣2x+180
D.y=﹣x+90
二.填空题(共8小题)
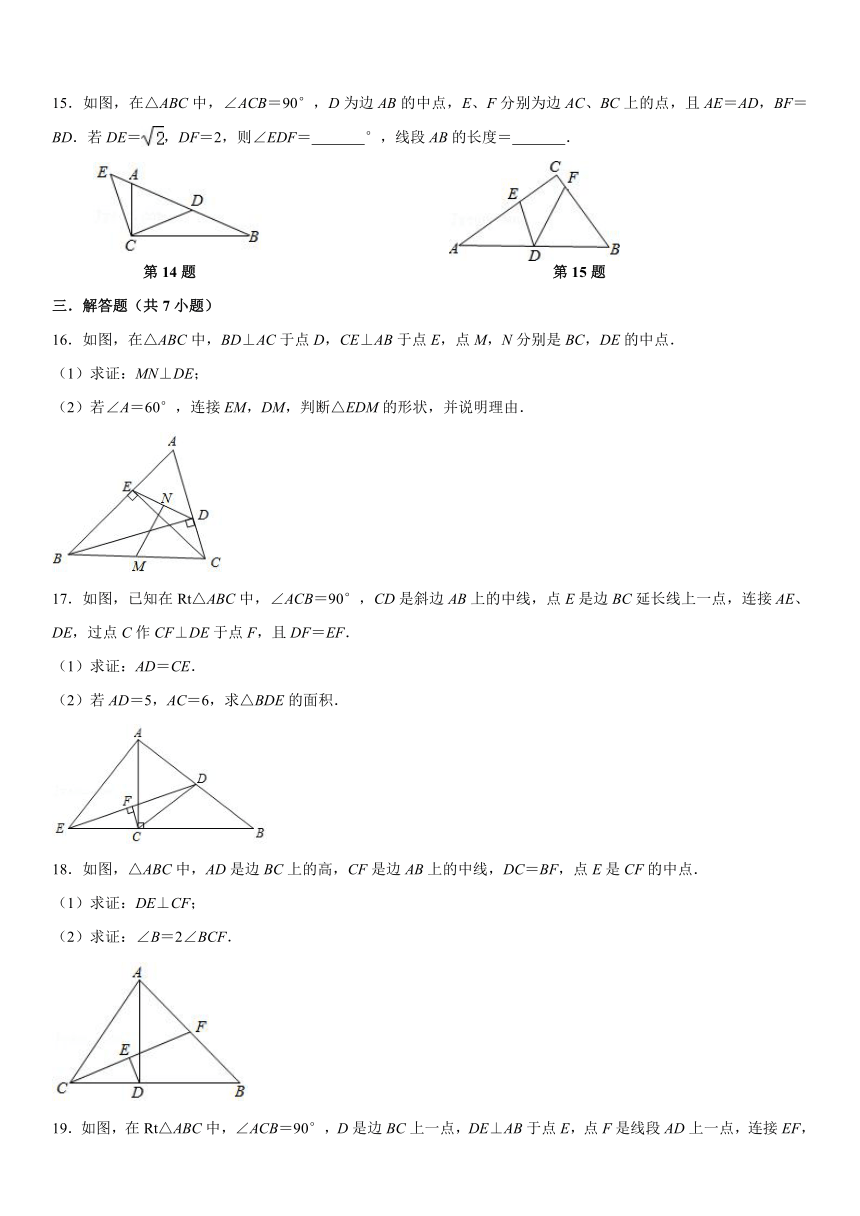
8.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为
.
9.如图,在Rt△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=10,BG=4,则CF的长为
.
10.在△ABC中,∠BAC为钝角,AF,CE都是这个三角形的高,P为AC的中点,若∠B=42°,则∠EPF的度数为
.
第8题
第9题
第10题
11.如图,△ABC中,AB=AC=4,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED=
.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,M为AB边的中点,连接ME、MD、ED,设AB=10,∠DBE=30°,则△EDM的面积为
.
13.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=
.
第11题
第12题
第13题
14.如图,在△ABC中,∠ACB=90°,D是AB的中点,以点C为圆心,CD长为半径画弧交BA的延长线于点E,设∠B=x,∠ACE=y.则y与x的关系式为
.
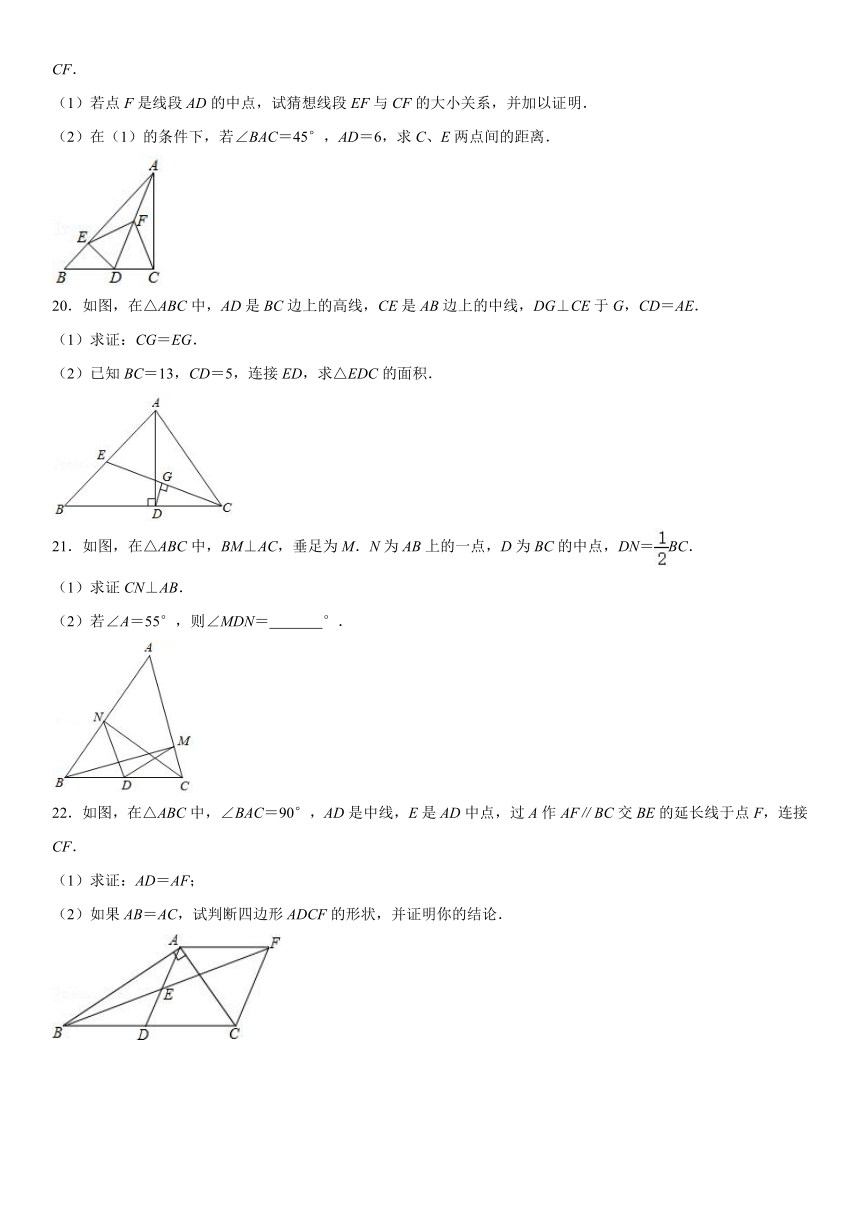
15.如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE=,DF=2,则∠EDF=
°,线段AB的长度=
.
第14题
第15题
三.解答题(共7小题)
16.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,点M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若∠A=60°,连接EM,DM,判断△EDM的形状,并说明理由.
17.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若AD=5,AC=6,求△BDE的面积.
18.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.
(1)求证:DE⊥CF;
(2)求证:∠B=2∠BCF.
19.如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
(1)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(2)在(1)的条件下,若∠BAC=45°,AD=6,求C、E两点间的距离.
20.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC=13,CD=5,连接ED,求△EDC的面积.
21.如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN=
°.
22.如图,在△ABC中,∠BAC=90°,AD是中线,E是AD中点,过A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
1.2.2直角三角形斜边上的中线
参考答案与试题解析
一.选择题(共7小题)
1.如图所示,公路AC,BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为5km,则M,C两点间的距离为( )
A.2.5km
B.3km
C.4.5km
D.5km
【解答】解:∵公路AC,BC互相垂直,
∴∠ACB=90°,
∵M为AB的中点,
∴CM=AB,
∵AB=5km,
∴CM=2.5(km),
即M,C两点间的距离为2.5km,
故选:A.
2.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为( )
A.3
B.4
C.5
D.6
【解答】解:∵AB=AC=8,AD是角平分线,
∴AD⊥BC,
∴∠ADC=90°,
∵BE是中线,
∴AE=CE,
∴DE=AC=×8=4,
故选:B.
3.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=( )
A.2
B.3
C.4
D.6
【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,
∴AE=CE=10,
∵AD=2,
∴DE=8,
∵CD为AB边上的高,
在Rt△CDE中,CD===6,
故选:D.
4.如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
【解答】解:连接DE,
∵∠ADC=90°,E是AC的中点,
∴DE=AC=AE,
∴∠EDA=∠DAC=45°,
∴∠DEC=∠EDA+∠DAC=90°,
同理,∠BEC=60°,
∴∠DEB=90°+60°=150°,
∵DE=AC,BE=AC,
∴DE=BE,
∴∠DBE=×(180°﹣150°)=15°,
故选:C.
5.如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19°
B.33°
C.34°
D.43°
【解答】解:∵∠ABC=90°,BE为AC边上的中线,
∴∠BAC=90°﹣∠C=90°﹣52°=38°,BE=AC=AE=CE,
∴∠EBC=∠C=52°,
∵AD平分∠BAC,
∴∠CAD=∠BAC=19°,
∴∠ADB=∠C+∠DAC=52°+19°=71°,
∵BF⊥AD,
∴∠BFD=90°,
∴∠FBD=90°﹣∠ADB=19°,
∴∠EBF=∠EBC﹣∠FBD=52°﹣19°=33°;
故选:B.
6.如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )
A.2
B.
C.8
D.9
【解答】解:连接EF、DF,
∵BD⊥AC,F为BC的中点,
∴DF=BC=9,
同理,EF=BC=9,
∴FE=FD,又G为DE的中点,
∴FG⊥DE,GE=GD=DE=5,
由勾股定理得,FG==2,
故选:A.
7.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D;点F是AB的中点,连接DF,EF,设∠DFE=x°,∠ACB=y°,则( )
A.y=x
B.y=﹣x+90
C.y=﹣2x+180
D.y=﹣x+90
【解答】解:∵AE⊥BC于点E,BD⊥AC于点D;
∴∠ADB=∠BEA=90°,
∵点F是AB的中点,
∴AF=DF,BF=EF,
∴∠DAF=∠ADF,∠EBF=∠BEF,
∴∠AFD=180°﹣2∠CAB,∠BFE=180°﹣2∠ABC,
∴x°=180°﹣∠AFD﹣∠BFE=2(∠CAB+∠CBA)﹣180°=2(180°﹣y°)﹣180°=180°﹣2y°,
∴y=﹣x+90,
故选:B.
二.填空题(共8小题)
8.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为
4 .
【解答】解:∵AB=AC,AD是角平分线,
∴AD⊥BC,
∴∠ADC=90°,
∵BE是中线,
∴AE=CE,
∴DE=AC=×8=4,
故答案为:4.
9.如图,在Rt△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=10,BG=4,则CF的长为 2 .
【解答】解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵BD为AC边上的中线,∠ABC=90°,
∴BD=DF=AC,
∴四边形BGFD是菱形,
∴BD=DF=GF=BG=4,则AF=AG﹣GF=10﹣4=6,AC=2BD=8,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即62+CF2=82,
解得:CF=2.
故答案是:2.
10.在△ABC中,∠BAC为钝角,AF,CE都是这个三角形的高,P为AC的中点,若∠B=42°,则∠EPF的度数为 96° .
【解答】解:∵CE⊥BA,∠B=42°,
∴∠BCE=48°,
∵AF⊥BC,CE⊥BA,P为AC的中点,
∴PF=AC=PC,PE=AC=PC,
∴∠PFC=∠PCF,∠PEC=∠PCE,
∴∠EPF=2∠PCF+2∠PCE=2∠BCE=96°,
故答案为:96°.
11.如图,△ABC中,AB=AC=4,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED= 2 .
【解答】解:∵∠ADC=90°,∠CAD=30°,F是AC的中点,
∴DF=AF=AC=,
∴∠FDA=∠CAD=30°,
∴∠DFC=∠FDA+∠CAD=60°
∵E、F分别是BC、AC的中点,
∴EF∥AB,EF=AB==2,
∴∠EFC=∠CAB=30°,
∴∠EFD=60°+30°=90°,
∴ED==2.
故答案为:2.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,M为AB边的中点,连接ME、MD、ED,设AB=10,∠DBE=30°,则△EDM的面积为 .
【解答】解:∵在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,
∴△ABE,△ADB是直角三角形,
∴EM,DM分别是它们斜边上的中线,
∴EM=DM=AB=5,
∵ME=AB=MA,
∴∠MAE=∠MEA,
∴∠BME=2∠MAE,
同理,MD=AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME﹣∠BMD=2∠MAE﹣2∠MAD=2∠DAC=60°,
∴△EDM是边长为5的等边三角形,
∴S△EDM=×52=.
故答案为:.
13.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO= 90° .
【解答】解:连接EB、ED,
∵∠ABC=90°,E是AC的中点,
∴BE=AC,
同理,DE=AC,
∴EB=ED,又F是BD的中点,
∴EF⊥BD,
∴∠EFO=90°,
故答案为:90°.
14.如图,在△ABC中,∠ACB=90°,D是AB的中点,以点C为圆心,CD长为半径画弧交BA的延长线于点E,设∠B=x,∠ACE=y.则y与x的关系式为 y=90°﹣3x .
【解答】解:∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD,
∴∠DCB=∠B=x,
∴∠ADC=2x,
∵CE=CD,
∴∠E=∠ADC=2x,
∵∠EAC=∠ACB+∠B=90°+x,
∴y=180°﹣∠E﹣∠EAC=180°﹣2x﹣(90°+x)=90°﹣3x,
即y与x的关系式为:y=90°﹣3x,
故答案为:y=90°﹣3x.
15.如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE=,DF=2,则∠EDF= 45 °,线段AB的长度= 2 .
【解答】解:如图,延长FD到M使得DM=DF,连接AM、EM、EF,作EN⊥DF于N.
∵∠C=90°,
∴∠BAC+∠B=90°,
∵AE=AD,BF=BD,
∴∠AED=∠ADE,∠BDF=∠BFD,
∴2∠ADE+∠BAC=180°,2∠BDF+∠B=180°,
∴2∠ADE+2∠BDF=270°,
∴∠ADE+∠BDF=135°,
∴∠EDF=180°﹣(∠ADE+∠BDF)=45°,
∵∠END=90°,DE=,
∴∠EDF=∠DEN=45°,
∴EN=DN=1,
在△DAM和△DBF中,
,
∴△ADM≌△BDF(SAS),
∴BF=AM=BD=AD=AE,∠MAD=∠B,
∴∠MAE=∠MAD+∠BAC=90°,
∴EM=AM,
在Rt△EMN中,∵EN=1,MN=DM+DN=3,
∴EM==,
∴AM=,AB=2AM=2.
故答案为:45,2.
三.解答题(共7小题)
16.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,点M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若∠A=60°,连接EM,DM,判断△EDM的形状,并说明理由.
【解答】(1)证明:连接ME,MD.
∵BD⊥AC于D,CE⊥AB于E,点M是BC的中点,
∴MD=ME=BC,
∴点N是DE的中点,
∴MN⊥DE;
(2)解:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB),
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∴∠BME+∠CMD=360°﹣2×120°=120°,
∴∠DME=60°,
∴△EDM是等边三角形.
17.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若AD=5,AC=6,求△BDE的面积.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=AB,
∵CF⊥DE,DF=EF.
∴CE=CD,
∴AD=CE.
(2)解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,AD=5,
∴AB=2AD=10,
∵AC=6,
∴BC==8,
由(1)知,CE=CD=AD=5,
∴BE=BC+EC=13,
∴S△ABE=BE?AC=,
∵点D是AB的中点,
∴△BDE的面积=S△ABE=.
18.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.
(1)求证:DE⊥CF;
(2)求证:∠B=2∠BCF.
【解答】证明:(1)连接DF,
∵AD是边BC上的高,
∴∠ADB=90°,
∵点F是AB的中点,
∴DF=AB=BF,
∵DC=BF,
∴DC=DF,
∵点E是CF的中点.
∴DE⊥CF;
(2)∵DC=DF,
∴∠DFC=∠DCF,
∴∠FDB=∠DFC+∠DCF=2∠DFC,
∵DF=BF,
∴∠FDB=∠B,
∴∠B=2∠BCF.
19.如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
(1)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(2)在(1)的条件下,若∠BAC=45°,AD=6,求C、E两点间的距离.
【解答】解:(1)EF=CF.
证明:∵DE⊥AB,
∴∠DEA=90°,
在Rt△AED和Rt△ACD中,
∵点F是斜边AD的中点,
∴EF=AD,CF=AD,
∴EF=CF;
(2)连接CE,由(1)得EF=AF=CF=AD=3,
∴∠FEA=∠FAE,∠FCA=∠FAC,
∴∠EFC=2∠FAE+2∠FAC=2∠BAC=2×45°=90°,
∴CE===.
20.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC=13,CD=5,连接ED,求△EDC的面积.
【解答】(1)证明:连接DE,
在Rt△ADB中,点E是AB的中点,
∴DE=AB=AE,
∵CD=AE,
∴DE=DC,又DG⊥CE,
∴CG=EG.
(2)解:作EF⊥BC于F,
∵BC=13,CD=5,
∴BD=13﹣5=8,
∵DE=BE,EF⊥BC,
∴DF=BF=4,
∴EF===3,
∴△EDC的面积=×CD×EF=×5×3=7.5.
21.如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN= 70 °.
【解答】(1)证明:∵BM⊥AC,点D是BC的中点,
∴BD=CD=DM=BC,
∵DN=BC,
∴DM=DN=BD=CD,
∴∠DBN=∠BND,∠DNC=∠DCN,
∵∠NBD+∠BNC+∠NCD=180°,
∴2∠BND+2∠CND=180°,
∴∠BND+∠CND=90°,
即∠CNB=90°,
∴CN⊥AB;
(2)解:∵BM⊥AC,CN⊥AB,
∴∠BNC=∠BMC=90°,
∵D为BC的中点,
∴DN=BD,DM=CD,
∴∠BND=∠NBD,∠DMC=∠MCD,
∴∠BND+∠DMC=∠ABC+∠ACB=180°﹣∠A=125°,
∴∠AND+∠AMD=360°﹣125°=235°,
∴∠MDN=360°﹣∠A﹣∠AND﹣∠AMD=70°,
故答案为:70.
22.如图,在△ABC中,∠BAC=90°,AD是中线,E是AD中点,过A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
【解答】(1)证明:∵AF∥BC,
∴∠EAF=∠EDB,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,,
∴△AEF≌△DEB(ASA),
∴AF=BD,
∵在△ABC中,∠BAC=90°,AD是中线,
∴AD=BD=DC=BC,
∴AD=AF;
(2)当AB=AC时,四边形ADCF是正方形.
∵AF=BD=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是中线,
∴AD⊥BC,
∵AD=AF,
∴四边形ADCF是正方形
一.选择题(共7小题)
1.如图所示,公路AC,BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为5km,则M,C两点间的距离为( )
A.2.5km
B.3km
C.4.5km
D.5km
2.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为( )
A.3
B.4
C.5
D.6
3.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=( )
A.2
B.3
C.4
D.6
第1题
第2题
第3题
4.如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
5.如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19°
B.33°
C.34°
D.43°
6.如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )
A.2
B.
C.8
D.9
第4题
第5题
第6题
7.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D;点F是AB的中点,连接DF,EF,设∠DFE=x°,∠ACB=y°,则( )
A.y=x
B.y=﹣x+90
C.y=﹣2x+180
D.y=﹣x+90
二.填空题(共8小题)
8.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为
.
9.如图,在Rt△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=10,BG=4,则CF的长为
.
10.在△ABC中,∠BAC为钝角,AF,CE都是这个三角形的高,P为AC的中点,若∠B=42°,则∠EPF的度数为
.
第8题
第9题
第10题
11.如图,△ABC中,AB=AC=4,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED=
.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,M为AB边的中点,连接ME、MD、ED,设AB=10,∠DBE=30°,则△EDM的面积为
.
13.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=
.
第11题
第12题
第13题
14.如图,在△ABC中,∠ACB=90°,D是AB的中点,以点C为圆心,CD长为半径画弧交BA的延长线于点E,设∠B=x,∠ACE=y.则y与x的关系式为
.
15.如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE=,DF=2,则∠EDF=
°,线段AB的长度=
.
第14题
第15题
三.解答题(共7小题)
16.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,点M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若∠A=60°,连接EM,DM,判断△EDM的形状,并说明理由.
17.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若AD=5,AC=6,求△BDE的面积.
18.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.
(1)求证:DE⊥CF;
(2)求证:∠B=2∠BCF.
19.如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
(1)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(2)在(1)的条件下,若∠BAC=45°,AD=6,求C、E两点间的距离.
20.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC=13,CD=5,连接ED,求△EDC的面积.
21.如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN=
°.
22.如图,在△ABC中,∠BAC=90°,AD是中线,E是AD中点,过A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
1.2.2直角三角形斜边上的中线
参考答案与试题解析
一.选择题(共7小题)
1.如图所示,公路AC,BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为5km,则M,C两点间的距离为( )
A.2.5km
B.3km
C.4.5km
D.5km
【解答】解:∵公路AC,BC互相垂直,
∴∠ACB=90°,
∵M为AB的中点,
∴CM=AB,
∵AB=5km,
∴CM=2.5(km),
即M,C两点间的距离为2.5km,
故选:A.
2.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为( )
A.3
B.4
C.5
D.6
【解答】解:∵AB=AC=8,AD是角平分线,
∴AD⊥BC,
∴∠ADC=90°,
∵BE是中线,
∴AE=CE,
∴DE=AC=×8=4,
故选:B.
3.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=( )
A.2
B.3
C.4
D.6
【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,
∴AE=CE=10,
∵AD=2,
∴DE=8,
∵CD为AB边上的高,
在Rt△CDE中,CD===6,
故选:D.
4.如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
【解答】解:连接DE,
∵∠ADC=90°,E是AC的中点,
∴DE=AC=AE,
∴∠EDA=∠DAC=45°,
∴∠DEC=∠EDA+∠DAC=90°,
同理,∠BEC=60°,
∴∠DEB=90°+60°=150°,
∵DE=AC,BE=AC,
∴DE=BE,
∴∠DBE=×(180°﹣150°)=15°,
故选:C.
5.如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19°
B.33°
C.34°
D.43°
【解答】解:∵∠ABC=90°,BE为AC边上的中线,
∴∠BAC=90°﹣∠C=90°﹣52°=38°,BE=AC=AE=CE,
∴∠EBC=∠C=52°,
∵AD平分∠BAC,
∴∠CAD=∠BAC=19°,
∴∠ADB=∠C+∠DAC=52°+19°=71°,
∵BF⊥AD,
∴∠BFD=90°,
∴∠FBD=90°﹣∠ADB=19°,
∴∠EBF=∠EBC﹣∠FBD=52°﹣19°=33°;
故选:B.
6.如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )
A.2
B.
C.8
D.9
【解答】解:连接EF、DF,
∵BD⊥AC,F为BC的中点,
∴DF=BC=9,
同理,EF=BC=9,
∴FE=FD,又G为DE的中点,
∴FG⊥DE,GE=GD=DE=5,
由勾股定理得,FG==2,
故选:A.
7.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D;点F是AB的中点,连接DF,EF,设∠DFE=x°,∠ACB=y°,则( )
A.y=x
B.y=﹣x+90
C.y=﹣2x+180
D.y=﹣x+90
【解答】解:∵AE⊥BC于点E,BD⊥AC于点D;
∴∠ADB=∠BEA=90°,
∵点F是AB的中点,
∴AF=DF,BF=EF,
∴∠DAF=∠ADF,∠EBF=∠BEF,
∴∠AFD=180°﹣2∠CAB,∠BFE=180°﹣2∠ABC,
∴x°=180°﹣∠AFD﹣∠BFE=2(∠CAB+∠CBA)﹣180°=2(180°﹣y°)﹣180°=180°﹣2y°,
∴y=﹣x+90,
故选:B.
二.填空题(共8小题)
8.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为
4 .
【解答】解:∵AB=AC,AD是角平分线,
∴AD⊥BC,
∴∠ADC=90°,
∵BE是中线,
∴AE=CE,
∴DE=AC=×8=4,
故答案为:4.
9.如图,在Rt△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=10,BG=4,则CF的长为 2 .
【解答】解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵BD为AC边上的中线,∠ABC=90°,
∴BD=DF=AC,
∴四边形BGFD是菱形,
∴BD=DF=GF=BG=4,则AF=AG﹣GF=10﹣4=6,AC=2BD=8,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即62+CF2=82,
解得:CF=2.
故答案是:2.
10.在△ABC中,∠BAC为钝角,AF,CE都是这个三角形的高,P为AC的中点,若∠B=42°,则∠EPF的度数为 96° .
【解答】解:∵CE⊥BA,∠B=42°,
∴∠BCE=48°,
∵AF⊥BC,CE⊥BA,P为AC的中点,
∴PF=AC=PC,PE=AC=PC,
∴∠PFC=∠PCF,∠PEC=∠PCE,
∴∠EPF=2∠PCF+2∠PCE=2∠BCE=96°,
故答案为:96°.
11.如图,△ABC中,AB=AC=4,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED= 2 .
【解答】解:∵∠ADC=90°,∠CAD=30°,F是AC的中点,
∴DF=AF=AC=,
∴∠FDA=∠CAD=30°,
∴∠DFC=∠FDA+∠CAD=60°
∵E、F分别是BC、AC的中点,
∴EF∥AB,EF=AB==2,
∴∠EFC=∠CAB=30°,
∴∠EFD=60°+30°=90°,
∴ED==2.
故答案为:2.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,M为AB边的中点,连接ME、MD、ED,设AB=10,∠DBE=30°,则△EDM的面积为 .
【解答】解:∵在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,
∴△ABE,△ADB是直角三角形,
∴EM,DM分别是它们斜边上的中线,
∴EM=DM=AB=5,
∵ME=AB=MA,
∴∠MAE=∠MEA,
∴∠BME=2∠MAE,
同理,MD=AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME﹣∠BMD=2∠MAE﹣2∠MAD=2∠DAC=60°,
∴△EDM是边长为5的等边三角形,
∴S△EDM=×52=.
故答案为:.
13.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO= 90° .
【解答】解:连接EB、ED,
∵∠ABC=90°,E是AC的中点,
∴BE=AC,
同理,DE=AC,
∴EB=ED,又F是BD的中点,
∴EF⊥BD,
∴∠EFO=90°,
故答案为:90°.
14.如图,在△ABC中,∠ACB=90°,D是AB的中点,以点C为圆心,CD长为半径画弧交BA的延长线于点E,设∠B=x,∠ACE=y.则y与x的关系式为 y=90°﹣3x .
【解答】解:∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD,
∴∠DCB=∠B=x,
∴∠ADC=2x,
∵CE=CD,
∴∠E=∠ADC=2x,
∵∠EAC=∠ACB+∠B=90°+x,
∴y=180°﹣∠E﹣∠EAC=180°﹣2x﹣(90°+x)=90°﹣3x,
即y与x的关系式为:y=90°﹣3x,
故答案为:y=90°﹣3x.
15.如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE=,DF=2,则∠EDF= 45 °,线段AB的长度= 2 .
【解答】解:如图,延长FD到M使得DM=DF,连接AM、EM、EF,作EN⊥DF于N.
∵∠C=90°,
∴∠BAC+∠B=90°,
∵AE=AD,BF=BD,
∴∠AED=∠ADE,∠BDF=∠BFD,
∴2∠ADE+∠BAC=180°,2∠BDF+∠B=180°,
∴2∠ADE+2∠BDF=270°,
∴∠ADE+∠BDF=135°,
∴∠EDF=180°﹣(∠ADE+∠BDF)=45°,
∵∠END=90°,DE=,
∴∠EDF=∠DEN=45°,
∴EN=DN=1,
在△DAM和△DBF中,
,
∴△ADM≌△BDF(SAS),
∴BF=AM=BD=AD=AE,∠MAD=∠B,
∴∠MAE=∠MAD+∠BAC=90°,
∴EM=AM,
在Rt△EMN中,∵EN=1,MN=DM+DN=3,
∴EM==,
∴AM=,AB=2AM=2.
故答案为:45,2.
三.解答题(共7小题)
16.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,点M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若∠A=60°,连接EM,DM,判断△EDM的形状,并说明理由.
【解答】(1)证明:连接ME,MD.
∵BD⊥AC于D,CE⊥AB于E,点M是BC的中点,
∴MD=ME=BC,
∴点N是DE的中点,
∴MN⊥DE;
(2)解:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB),
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∴∠BME+∠CMD=360°﹣2×120°=120°,
∴∠DME=60°,
∴△EDM是等边三角形.
17.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若AD=5,AC=6,求△BDE的面积.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=AB,
∵CF⊥DE,DF=EF.
∴CE=CD,
∴AD=CE.
(2)解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,AD=5,
∴AB=2AD=10,
∵AC=6,
∴BC==8,
由(1)知,CE=CD=AD=5,
∴BE=BC+EC=13,
∴S△ABE=BE?AC=,
∵点D是AB的中点,
∴△BDE的面积=S△ABE=.
18.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.
(1)求证:DE⊥CF;
(2)求证:∠B=2∠BCF.
【解答】证明:(1)连接DF,
∵AD是边BC上的高,
∴∠ADB=90°,
∵点F是AB的中点,
∴DF=AB=BF,
∵DC=BF,
∴DC=DF,
∵点E是CF的中点.
∴DE⊥CF;
(2)∵DC=DF,
∴∠DFC=∠DCF,
∴∠FDB=∠DFC+∠DCF=2∠DFC,
∵DF=BF,
∴∠FDB=∠B,
∴∠B=2∠BCF.
19.如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
(1)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(2)在(1)的条件下,若∠BAC=45°,AD=6,求C、E两点间的距离.
【解答】解:(1)EF=CF.
证明:∵DE⊥AB,
∴∠DEA=90°,
在Rt△AED和Rt△ACD中,
∵点F是斜边AD的中点,
∴EF=AD,CF=AD,
∴EF=CF;
(2)连接CE,由(1)得EF=AF=CF=AD=3,
∴∠FEA=∠FAE,∠FCA=∠FAC,
∴∠EFC=2∠FAE+2∠FAC=2∠BAC=2×45°=90°,
∴CE===.
20.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC=13,CD=5,连接ED,求△EDC的面积.
【解答】(1)证明:连接DE,
在Rt△ADB中,点E是AB的中点,
∴DE=AB=AE,
∵CD=AE,
∴DE=DC,又DG⊥CE,
∴CG=EG.
(2)解:作EF⊥BC于F,
∵BC=13,CD=5,
∴BD=13﹣5=8,
∵DE=BE,EF⊥BC,
∴DF=BF=4,
∴EF===3,
∴△EDC的面积=×CD×EF=×5×3=7.5.
21.如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN= 70 °.
【解答】(1)证明:∵BM⊥AC,点D是BC的中点,
∴BD=CD=DM=BC,
∵DN=BC,
∴DM=DN=BD=CD,
∴∠DBN=∠BND,∠DNC=∠DCN,
∵∠NBD+∠BNC+∠NCD=180°,
∴2∠BND+2∠CND=180°,
∴∠BND+∠CND=90°,
即∠CNB=90°,
∴CN⊥AB;
(2)解:∵BM⊥AC,CN⊥AB,
∴∠BNC=∠BMC=90°,
∵D为BC的中点,
∴DN=BD,DM=CD,
∴∠BND=∠NBD,∠DMC=∠MCD,
∴∠BND+∠DMC=∠ABC+∠ACB=180°﹣∠A=125°,
∴∠AND+∠AMD=360°﹣125°=235°,
∴∠MDN=360°﹣∠A﹣∠AND﹣∠AMD=70°,
故答案为:70.
22.如图,在△ABC中,∠BAC=90°,AD是中线,E是AD中点,过A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
【解答】(1)证明:∵AF∥BC,
∴∠EAF=∠EDB,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,,
∴△AEF≌△DEB(ASA),
∴AF=BD,
∵在△ABC中,∠BAC=90°,AD是中线,
∴AD=BD=DC=BC,
∴AD=AF;
(2)当AB=AC时,四边形ADCF是正方形.
∵AF=BD=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是中线,
∴AD⊥BC,
∵AD=AF,
∴四边形ADCF是正方形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
