4.1 几何图形(第1课时) 认识几何图形课件 2021-2022学年人教版数学 七年级上册(39张)
文档属性
| 名称 | 4.1 几何图形(第1课时) 认识几何图形课件 2021-2022学年人教版数学 七年级上册(39张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 08:43:12 | ||
图片预览




文档简介
4.1 几何图形
人教版· 数学· 七年级(上)
第四章 几何图形初步
第1课时 认识几何图形
1.能从简单实物的外形中抽象出几何图形,并了解立体图形与平面图形的区别。(难点)
2.会判断一个图形是立体图形还是平面图形,能准确识别简单几何体。(重点)
学习目标
从城市建筑到乡村住宅,从立交桥到交通标志,从剪纸艺术到城市雕塑,从动物形态到申奥标志……图形世界是多姿多彩的!
物体的形状、大小和位置关系是几何研究的内容.
导入新知
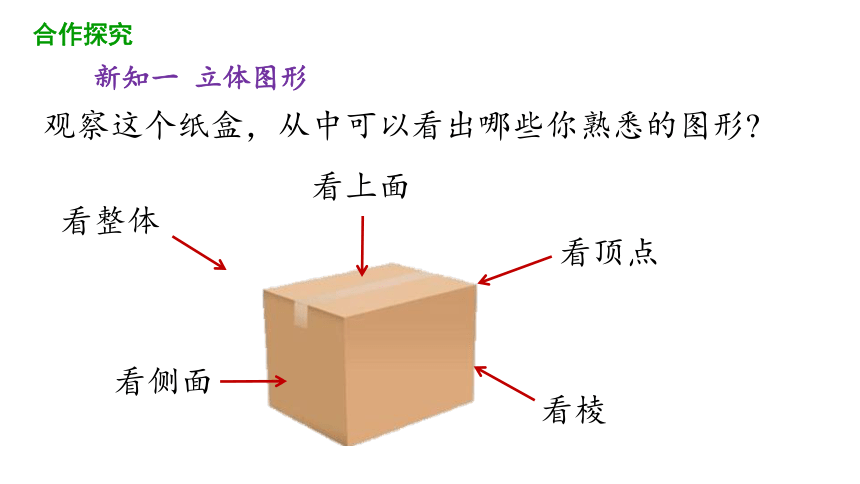
观察这个纸盒,从中可以看出哪些你熟悉的图形?
看整体
看侧面
看上面
看棱
看顶点
新知一 立体图形
合作探究
.
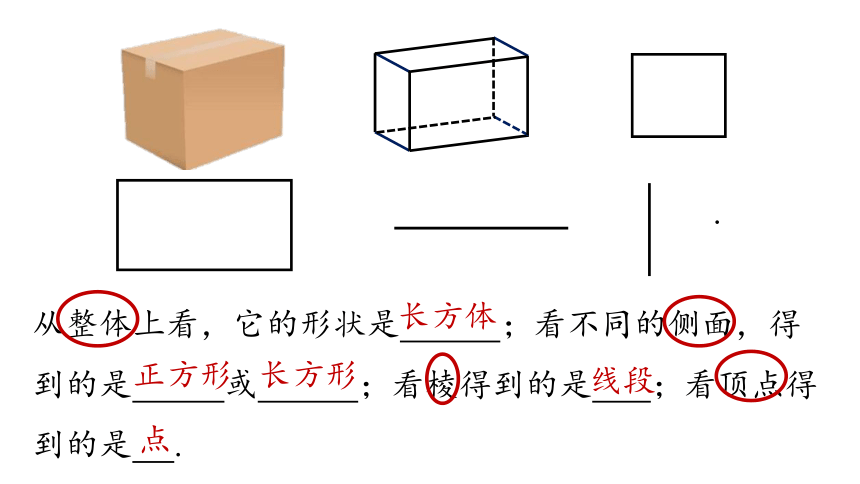
从整体上看,它的形状是 ;看不同的侧面,得到的是 或 ;看棱得到的是 ;看顶点得到的是 .
长方体
正方形
长方形
线段
点
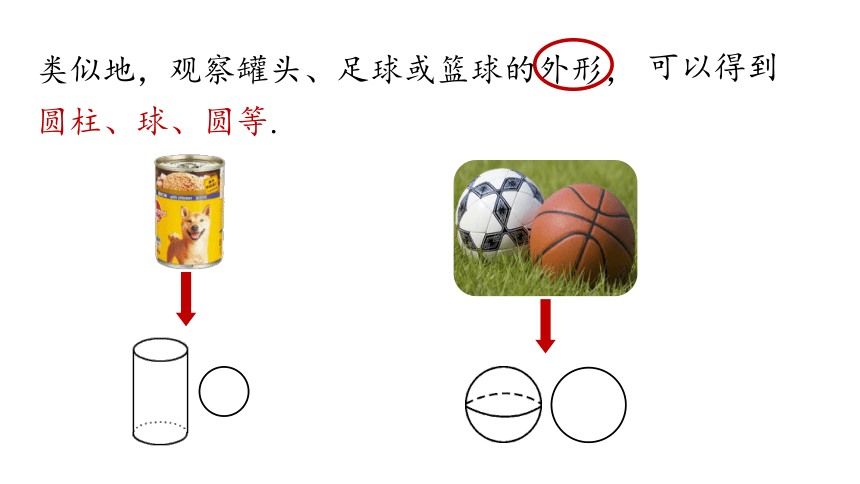
类似地,观察罐头、足球或篮球的外形,
可以得到
圆柱、球、圆等.
长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学过的三角形、四边形等,都是从物体外形中得出的,它们都是几何图形.
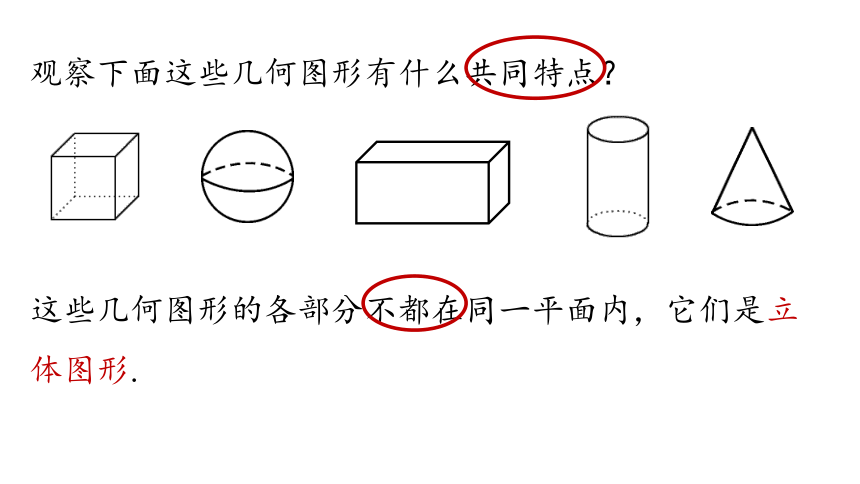
观察下面这些几何图形有什么共同特点?
这些几何图形的各部分不都在同一平面内,它们是立体图形.
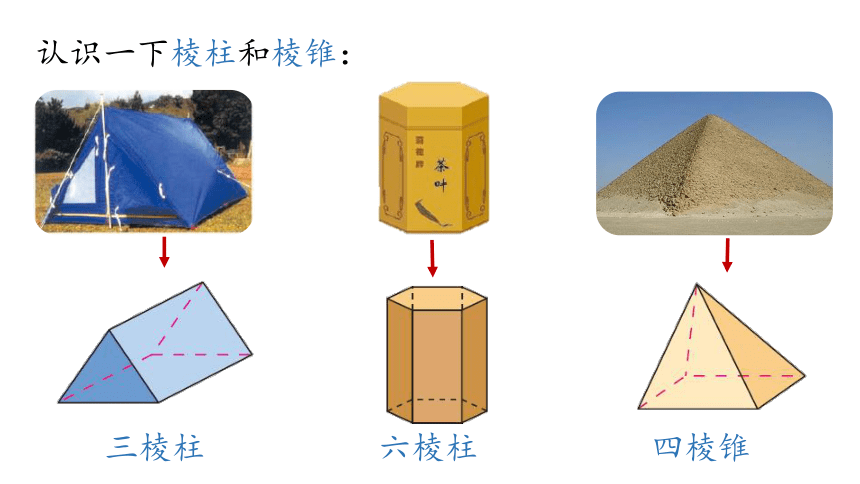
认识一下棱柱和棱锥:
三棱柱
四棱锥
六棱柱
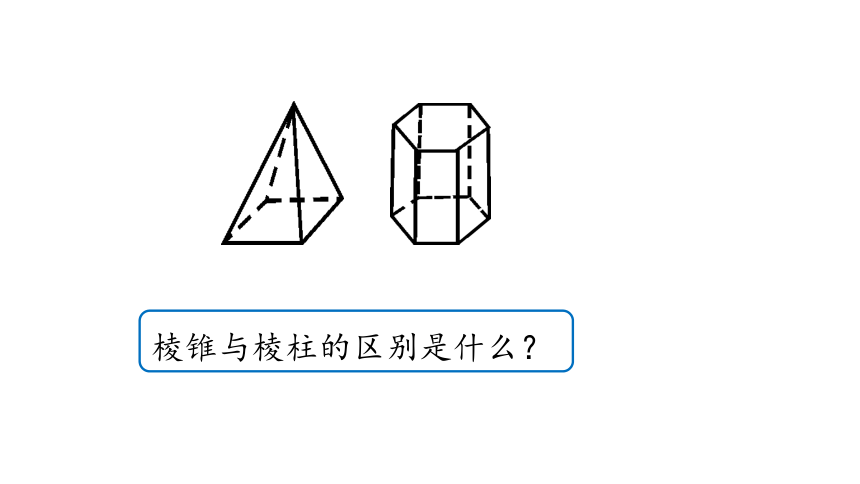
棱锥与棱柱的区别是什么?
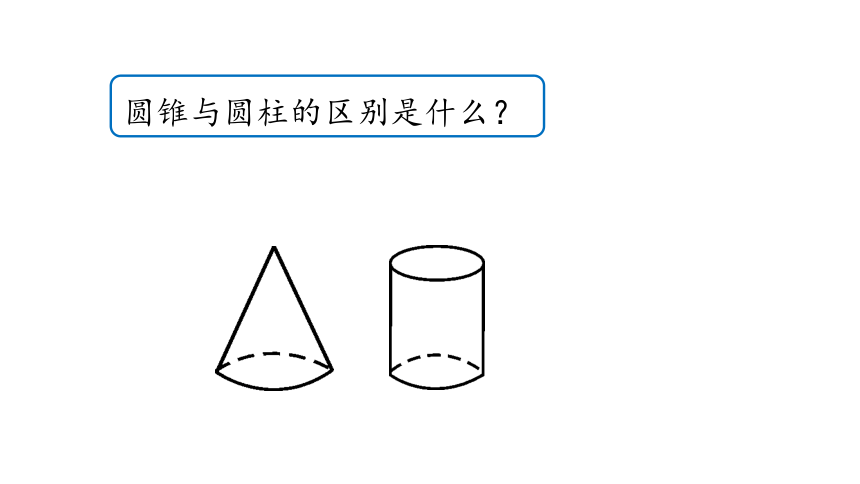
圆锥与圆柱的区别是什么?
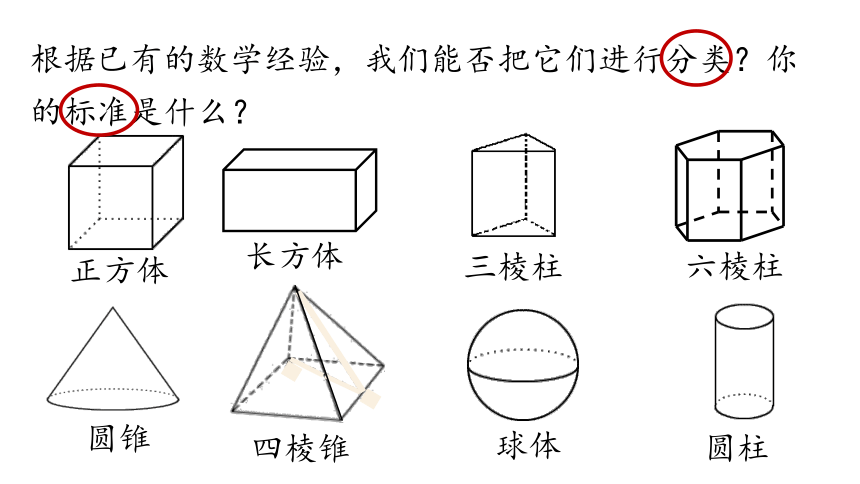
根据已有的数学经验,我们能否把它们进行分类?你的标准是什么?
圆锥
球体
圆柱
长方体
正方体
三棱柱
六棱柱
四棱锥
例1 请写出下列几何体的名称.
长方体
(或四棱柱)
圆柱
三棱锥
圆锥
三棱柱
巩固新知
说一说下面这些几何图形有什么共同特点?
这些几何图形的各部分都在同一平面内,它们是平面图形.
新知二 平面图形
合作探究
下面各图中包含哪些简单的平面图形?请再举出一些平面图形的例子.
长方形
圆
正方形、圆、
三角形、长方形
正方形、三角形
圆、线段、梯形
三角形、正方形
用两个圆、两个三角形和两条直线为条件,画出一个独特且具有意义的图形,并命名.
吊 灯
眼 镜
路 灯
落日余晖
虽然立体图形与平面图形是两类不同的几何图形,但它们是互相联系的.立体图形中某些部分是平面图形,例如长方体的侧面是长方形或正方形.
例2 下面各图中主要由哪些简单的平面图形组成?
解:图(1)由长方形和正方形组成;
图(2)由四边形(或菱形)组成;
图(3)由圆和圆弧组成.
(1)
(2)
(3)
巩固新知
1.图中实物的形状对应哪些立体图形?把相应的实物与图形用线连接起来.
课堂练习
2.如图,你能看到哪些立体图形?
球
长方体
圆柱
正方体
3.如图,你能看到哪些平面图形?
圆
三角形
正六边形
正五边形
长方形
正方形
立体图形
柱体
球体
圆柱
棱柱
三棱柱
四棱柱
五棱柱
…
几何图形
平面图形
圆、线段、角、多边形…
锥体
圆锥
棱锥
归纳新知
1.下列几何图形是立体图形的是( )
A.长方形
B.正方形
C.长方体
D.三角形
C
课后练习
2.下面几何体是圆柱的是( )
D
3.在几何图形:线段、圆、圆锥、正方体、角、棱锥中,属于立体图形的共有_____个.
3
4.观察下列几何图形,写出几何图形的名称.
5.把下列物体和与其对应的立体图形连接起来.
6.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
C
7.如图所示的两个几何体中存在的平面图形中没有( )
D
8.图中哪些图形是立体图形,哪些是平面图形?
解:立体图形是:①④⑤⑥⑦;平面图形是:②③⑧.
9.下面物体中,最接近圆柱的是( )
C
10.在下图中,和另外三个立体图形不同类的是( )
B
11.如图几何体的下部是一个三棱柱,下列各多边形与这个几何体的各面(包括底面)形状不相符的是( )
A
12.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱
C.三棱锥 D.四棱锥
D
13.如图是一座粮仓,它可以看作是由几何体_____和______组成的.
圆锥
圆柱
14.观察图中的表格,回答下列问题:
(1)表格中有哪些平面图形?
(2)你可以发现什么样的变化规律?
(3)图中有一处遗漏的图形,请你补充.
解:(1)圆、平行四边形、正方形、半圆、三角形、长方形、扇形.
(2)从上到下,下面的图形是其上面的图形对折得到的.
(3)略.
15.将图中的几何体分类,并说明理由.
解:①②③⑦属于柱体;⑤⑥属于锥体;④属于球.
16.红星中学七(1)班的李老师在上完“几何图形”第一课时后,给班上的同学们出了这样一道思考题:用六根火柴棒,你能组成四个大小一样的三角形吗?若能,叙述你的做法;若不能,请说明理由.
小明的解答是:不能.因为三根火柴棒只能摆出一个三角形,五根火柴棒可摆出两个三角形(如图所示),六根火柴棒根本不可能摆出四个大小完全相同的三角形.
你认为小明的解答正确吗?若不正确,试通过画图进行说明.
解:小明的解答不正确,可以摆成一个三棱锥,正好能组成四个大小一样的三角形,画图略.
再
见
人教版· 数学· 七年级(上)
第四章 几何图形初步
第1课时 认识几何图形
1.能从简单实物的外形中抽象出几何图形,并了解立体图形与平面图形的区别。(难点)
2.会判断一个图形是立体图形还是平面图形,能准确识别简单几何体。(重点)
学习目标
从城市建筑到乡村住宅,从立交桥到交通标志,从剪纸艺术到城市雕塑,从动物形态到申奥标志……图形世界是多姿多彩的!
物体的形状、大小和位置关系是几何研究的内容.
导入新知
观察这个纸盒,从中可以看出哪些你熟悉的图形?
看整体
看侧面
看上面
看棱
看顶点
新知一 立体图形
合作探究
.
从整体上看,它的形状是 ;看不同的侧面,得到的是 或 ;看棱得到的是 ;看顶点得到的是 .
长方体
正方形
长方形
线段
点
类似地,观察罐头、足球或篮球的外形,
可以得到
圆柱、球、圆等.
长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学过的三角形、四边形等,都是从物体外形中得出的,它们都是几何图形.
观察下面这些几何图形有什么共同特点?
这些几何图形的各部分不都在同一平面内,它们是立体图形.
认识一下棱柱和棱锥:
三棱柱
四棱锥
六棱柱
棱锥与棱柱的区别是什么?
圆锥与圆柱的区别是什么?
根据已有的数学经验,我们能否把它们进行分类?你的标准是什么?
圆锥
球体
圆柱
长方体
正方体
三棱柱
六棱柱
四棱锥
例1 请写出下列几何体的名称.
长方体
(或四棱柱)
圆柱
三棱锥
圆锥
三棱柱
巩固新知
说一说下面这些几何图形有什么共同特点?
这些几何图形的各部分都在同一平面内,它们是平面图形.
新知二 平面图形
合作探究
下面各图中包含哪些简单的平面图形?请再举出一些平面图形的例子.
长方形
圆
正方形、圆、
三角形、长方形
正方形、三角形
圆、线段、梯形
三角形、正方形
用两个圆、两个三角形和两条直线为条件,画出一个独特且具有意义的图形,并命名.
吊 灯
眼 镜
路 灯
落日余晖
虽然立体图形与平面图形是两类不同的几何图形,但它们是互相联系的.立体图形中某些部分是平面图形,例如长方体的侧面是长方形或正方形.
例2 下面各图中主要由哪些简单的平面图形组成?
解:图(1)由长方形和正方形组成;
图(2)由四边形(或菱形)组成;
图(3)由圆和圆弧组成.
(1)
(2)
(3)
巩固新知
1.图中实物的形状对应哪些立体图形?把相应的实物与图形用线连接起来.
课堂练习
2.如图,你能看到哪些立体图形?
球
长方体
圆柱
正方体
3.如图,你能看到哪些平面图形?
圆
三角形
正六边形
正五边形
长方形
正方形
立体图形
柱体
球体
圆柱
棱柱
三棱柱
四棱柱
五棱柱
…
几何图形
平面图形
圆、线段、角、多边形…
锥体
圆锥
棱锥
归纳新知
1.下列几何图形是立体图形的是( )
A.长方形
B.正方形
C.长方体
D.三角形
C
课后练习
2.下面几何体是圆柱的是( )
D
3.在几何图形:线段、圆、圆锥、正方体、角、棱锥中,属于立体图形的共有_____个.
3
4.观察下列几何图形,写出几何图形的名称.
5.把下列物体和与其对应的立体图形连接起来.
6.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
C
7.如图所示的两个几何体中存在的平面图形中没有( )
D
8.图中哪些图形是立体图形,哪些是平面图形?
解:立体图形是:①④⑤⑥⑦;平面图形是:②③⑧.
9.下面物体中,最接近圆柱的是( )
C
10.在下图中,和另外三个立体图形不同类的是( )
B
11.如图几何体的下部是一个三棱柱,下列各多边形与这个几何体的各面(包括底面)形状不相符的是( )
A
12.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱
C.三棱锥 D.四棱锥
D
13.如图是一座粮仓,它可以看作是由几何体_____和______组成的.
圆锥
圆柱
14.观察图中的表格,回答下列问题:
(1)表格中有哪些平面图形?
(2)你可以发现什么样的变化规律?
(3)图中有一处遗漏的图形,请你补充.
解:(1)圆、平行四边形、正方形、半圆、三角形、长方形、扇形.
(2)从上到下,下面的图形是其上面的图形对折得到的.
(3)略.
15.将图中的几何体分类,并说明理由.
解:①②③⑦属于柱体;⑤⑥属于锥体;④属于球.
16.红星中学七(1)班的李老师在上完“几何图形”第一课时后,给班上的同学们出了这样一道思考题:用六根火柴棒,你能组成四个大小一样的三角形吗?若能,叙述你的做法;若不能,请说明理由.
小明的解答是:不能.因为三根火柴棒只能摆出一个三角形,五根火柴棒可摆出两个三角形(如图所示),六根火柴棒根本不可能摆出四个大小完全相同的三角形.
你认为小明的解答正确吗?若不正确,试通过画图进行说明.
解:小明的解答不正确,可以摆成一个三棱锥,正好能组成四个大小一样的三角形,画图略.
再
见
