5.2 求解一元一次方程(第2课时) 课件 2021-2022学年北师大版数学 七年级上册(36张)
文档属性
| 名称 | 5.2 求解一元一次方程(第2课时) 课件 2021-2022学年北师大版数学 七年级上册(36张) |  | |
| 格式 | pptx | ||
| 文件大小 | 563.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 08:45:09 | ||
图片预览











文档简介
5.2 求解一元一次方程
北师大版 · 数学· 七年级(上)
第五章 一元一次方程
第2课时 解带括号的一元一次方程
1.正确理解和使用去括号法则。
2.学会解带括号的一元一次方程。
3.体验用多种方法解一元一次方程,提高解一元一次方程的能力。
学习目标
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
分析:
设上半年每月平均用电量列出方程xkW·h,
则下半年每月平均用电为(x-2000) kW·h.
上半年共用电为:6x kW·h;
上半年共用电为:6(x-2000) kW·h.
根据题意列出方程
6x+6(x-2 000)=150 000
怎样解这个方程?
这就是我们今天要研究的问题!
导入新知
我要1听果奶饮料和4听可乐.
你给我10元,找你3元.
1听可乐比1听果奶饮料多0.5元.
1听果奶饮料多少钱呢?
如果设1听果奶饮料x元,那么可列出方程:
新知 利用去括号解一元一次方程
4(x+0.5)+x=10-3
合作探究
(1)上面这个方程列的对吗?你还能列出不同的方程吗
(2)上面的方程与上节课所解的方程有什么区别?你能解所列的方程吗?
思考:
4(x+0.5)+x=10-3
观察下面的方程,结合去括号法则,你能求得它的解吗?
4(x+0.5 )+x=10-3
方程的左边有带括号的式子,可以尝试去括号!赶快动手试一试吧!
交流探究
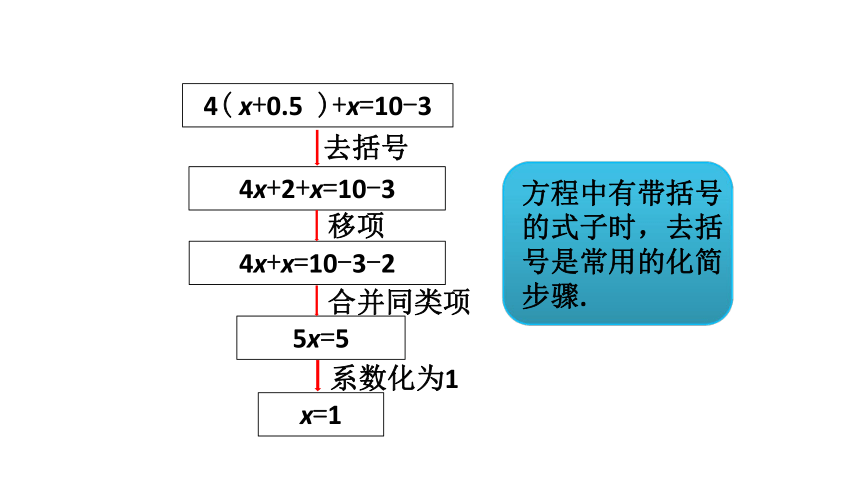
去括号
4( x+0.5 )+x=10-3
4x+2+x=10-3
4x+x=10-3-2
5x=5
x=1
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
解方程: 4(x+0.5)+x=7.
解:去括号, 得4x + 2 + x = 7,
移项, 得4x + x=7-2,
合并同类项, 得 5x = 5,
方程两边同除以5,得 x=1.
典例精析1 解含有括号的一元一次方程
例1
解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(1)2x-(x+10)=5x+2(x-1)
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
-6x=8
x=-????????
?
巩固新知
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(2)3x-7(x-1)=3-2(x+3)
3x-7x+7=3-2x-6
3x-7x+2x=3-6-7
-2x=-10
x=5
解方程:-2(x-1)=4
解法一:去括号,得-2x+2=4.
移项,得 -2x= 4-2.
化简,得 -2x=2.
系数化为1,得 x=-1.
解法二:方程两边同时除以-2,得x-1=-2
移项,得x=-2+1
化简,得x=-1
议一议
观察上述两种解法,
说出它们的区别.
第二种解法将x-1作为一个整体进行思考.
典例精析2 多种方法解一元一次方程
例2
合作探究
解方程:(1)2(x+0.5)+2x=45;(2)4(x+16)=-2(x+1).
分析:要解这两个方程可按去括号法则先将括号去掉,
然后按照移项法则移项,合并同类项,将未知数的系
数化为1,要注意符号问题.
巩固新知
(1)2(x+0.5)+2x=45
解:去括号,得 2x+1+2x=45.
移项,得 2x+2x=45-1.
合并同类项,得 4x=44.
系数化为1,得 x=11.
解:两边都除以2,得
2(x+16)=-(x+1).
去括号,得 2x+32=-x-1.
移项,得 2x+x=-1-32.
合并同类项,得 3x=-33.
系数化为1,得 x=-11.
(2)4(x+16)=-2(x+1).
误区警示:
(1)中2(x+0.5)变形时,2应乘括号内的每一项,不要只乘了一项,而漏乘其余各项,其变形的基础是乘法分配律;
(2)先根据等式的基本性质2,将方程两边都除以2,缩小数据,使解题简便.
1.解方程3-(x+6)=-5(x-1)时,去括号正确的是( )
A.3-x+6=-5x+5 B.3-x-6=-5x+5
C.3-x+6=-5x-5 D.3-x-6=-5x+1
B
2.方程6(x+2)=30的解与下列方程的解相同的是( )
A. x+2=30 B. x+2=????????
C.x+2=0 D.x-3=0
?
D
课堂练习
3. 解下列方程:
(1)5(x+4)=30; (2) 6(x-3)=42.
解:方程两边同除以5,得
x+4=6,
移项,得x=6-4,
即x=2.
解:方程两边同除以6,得
x-3=7,
移项,得 x=7+3,
即x=10.
去括号解一元一次方程
步骤
去括号注意
去括号→移项→合并同类项→系数化为1.
若括号外的因数是负数,去括号时,原括号内各项的符号要改变.
归纳新知
1.6(x-20)=_______________;-3(x+1)=_____________.
2.(2020·康定)解方程3-(x+6)=-5(x-1)时,去括号正确的是( )
A.3-x+6=-5x+5 B.3-x-6=-5x+5
C.3-x+6=-5x-5 D.3-x-6=-5x+1
6x-120
-3x-3
B
课后练习
3.方程3(x+1)-2(x-1)=1变形正确的是( )
A.3x+3-2x+2=1 B.3x+3-2x-2=1
C.3x+3+2x-2=1 D.3x+3-2x+1=1
A
B
5.方程2(x-1)=x+2的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
6.方程2(x-2)-3(4x-1)=9的解是( )
A.x=0.8 B.x=-1
C.x=-1.6 D.x=1
D
B
A
8.解方程:
(1)5(x+2)=2(5x-1);
(2)2(x-1)-(x+2)=3(4-x);
解:x=4
(3)2(3x-2)=5(x-2);
解:x=-6
(4)5(x+8)=6(2x-7)+5.
解:x=11
9.已知方程2(x-1)+1=x的解与关于x的方程3(x+m)=m-1的解相同,求m的值.
解:解方程2(x-1)+1=x得x=1,把x=1代入方程3(x+m)=m-1中得m=-2
10.某城市出租车的收费标准是:起步价7元(即行驶距离不超过3千米,都需付7元车费),超过3千米后,每增加1千米收费2.4元,不足1千米按1千米计,某人乘这种出租车从甲地到乙地刚好付19元车费,求甲、乙两地的距离?
解:设甲、乙两地的距离为x千米,根据题意,得7+2.4(x-3)=19,解得x=8,答:甲、乙两地的距离是8千米
10.解下列方程:
(1)3x-4=5-6x;
解:x=1
(2)7x+1.37=15x-0.23;
解:x=0.2
(3)4x+5=3x+3-2x;
(4)8x+16=52-4x.
解:x=3
11.解方程x-2(x-1)=4,去括号正确的是( )
A.x-2x-1=4 B.x-2x+2=4
C.x-2x-2=4 D.x-2x+1=4
12.方程4(a-x)-4(x+1)=60的解是x=1,则a的值为( )
A.-14 B.20 C.18 D.-16
B
C
13.如果a=3,那么a(x+1)=2(x+1)的解是( )
A.0 B.-1 C.无解 D.1
B
14.解下列方程:
(1)6y=2(1+y)-3(y+3);
解:y=-1
(2)2(m-3)-5(2m-1)=3(2m+1)-8;
(3)3(x-7)-2[9-4(2-x)]=22.
解:x=-9
15.已知方程2(x-1)=3(x+2)的解是m-5,求关于x的方程2[3(x-m)-4(x+1)]=3(m-2)的解.
17.若关于x的方程5x-a=4x+3的解比关于x的方程2(2x+a)+5=3(x+2)的解大8,求a的值.
解:解方程5x-a=4x+3得x=a+3,解方程2(2x+a)+5=3(x+2)得x=1-2a,因为方程5x-a=4x+3的解比方程2(2x+a)+5=3(x+2)的解大8,所以(a+3)-(1-2a)=8,解得a=2
18.(2019·海南模拟)海南五月瓜果飘香.某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
解:设李叔叔购买无核荔枝x千克,依题意得26x+22(30-x)=708.解得x=12,30-x=18.答:李叔叔购买这两种水果各12千克和18千克
19.在五一期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?说明理由.
解:(1)设一共去了x个成人,依题意得35x+0.5×35×(12-x)=350,解得x=8,12-x=4,答:他们一共去了8个成人,4个学生 (2)35×16×0.6=336(元),因为336<350,所以购买团体票更加省钱
再
见
北师大版 · 数学· 七年级(上)
第五章 一元一次方程
第2课时 解带括号的一元一次方程
1.正确理解和使用去括号法则。
2.学会解带括号的一元一次方程。
3.体验用多种方法解一元一次方程,提高解一元一次方程的能力。
学习目标
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
分析:
设上半年每月平均用电量列出方程xkW·h,
则下半年每月平均用电为(x-2000) kW·h.
上半年共用电为:6x kW·h;
上半年共用电为:6(x-2000) kW·h.
根据题意列出方程
6x+6(x-2 000)=150 000
怎样解这个方程?
这就是我们今天要研究的问题!
导入新知
我要1听果奶饮料和4听可乐.
你给我10元,找你3元.
1听可乐比1听果奶饮料多0.5元.
1听果奶饮料多少钱呢?
如果设1听果奶饮料x元,那么可列出方程:
新知 利用去括号解一元一次方程
4(x+0.5)+x=10-3
合作探究
(1)上面这个方程列的对吗?你还能列出不同的方程吗
(2)上面的方程与上节课所解的方程有什么区别?你能解所列的方程吗?
思考:
4(x+0.5)+x=10-3
观察下面的方程,结合去括号法则,你能求得它的解吗?
4(x+0.5 )+x=10-3
方程的左边有带括号的式子,可以尝试去括号!赶快动手试一试吧!
交流探究
去括号
4( x+0.5 )+x=10-3
4x+2+x=10-3
4x+x=10-3-2
5x=5
x=1
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
解方程: 4(x+0.5)+x=7.
解:去括号, 得4x + 2 + x = 7,
移项, 得4x + x=7-2,
合并同类项, 得 5x = 5,
方程两边同除以5,得 x=1.
典例精析1 解含有括号的一元一次方程
例1
解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(1)2x-(x+10)=5x+2(x-1)
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
-6x=8
x=-????????
?
巩固新知
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(2)3x-7(x-1)=3-2(x+3)
3x-7x+7=3-2x-6
3x-7x+2x=3-6-7
-2x=-10
x=5
解方程:-2(x-1)=4
解法一:去括号,得-2x+2=4.
移项,得 -2x= 4-2.
化简,得 -2x=2.
系数化为1,得 x=-1.
解法二:方程两边同时除以-2,得x-1=-2
移项,得x=-2+1
化简,得x=-1
议一议
观察上述两种解法,
说出它们的区别.
第二种解法将x-1作为一个整体进行思考.
典例精析2 多种方法解一元一次方程
例2
合作探究
解方程:(1)2(x+0.5)+2x=45;(2)4(x+16)=-2(x+1).
分析:要解这两个方程可按去括号法则先将括号去掉,
然后按照移项法则移项,合并同类项,将未知数的系
数化为1,要注意符号问题.
巩固新知
(1)2(x+0.5)+2x=45
解:去括号,得 2x+1+2x=45.
移项,得 2x+2x=45-1.
合并同类项,得 4x=44.
系数化为1,得 x=11.
解:两边都除以2,得
2(x+16)=-(x+1).
去括号,得 2x+32=-x-1.
移项,得 2x+x=-1-32.
合并同类项,得 3x=-33.
系数化为1,得 x=-11.
(2)4(x+16)=-2(x+1).
误区警示:
(1)中2(x+0.5)变形时,2应乘括号内的每一项,不要只乘了一项,而漏乘其余各项,其变形的基础是乘法分配律;
(2)先根据等式的基本性质2,将方程两边都除以2,缩小数据,使解题简便.
1.解方程3-(x+6)=-5(x-1)时,去括号正确的是( )
A.3-x+6=-5x+5 B.3-x-6=-5x+5
C.3-x+6=-5x-5 D.3-x-6=-5x+1
B
2.方程6(x+2)=30的解与下列方程的解相同的是( )
A. x+2=30 B. x+2=????????
C.x+2=0 D.x-3=0
?
D
课堂练习
3. 解下列方程:
(1)5(x+4)=30; (2) 6(x-3)=42.
解:方程两边同除以5,得
x+4=6,
移项,得x=6-4,
即x=2.
解:方程两边同除以6,得
x-3=7,
移项,得 x=7+3,
即x=10.
去括号解一元一次方程
步骤
去括号注意
去括号→移项→合并同类项→系数化为1.
若括号外的因数是负数,去括号时,原括号内各项的符号要改变.
归纳新知
1.6(x-20)=_______________;-3(x+1)=_____________.
2.(2020·康定)解方程3-(x+6)=-5(x-1)时,去括号正确的是( )
A.3-x+6=-5x+5 B.3-x-6=-5x+5
C.3-x+6=-5x-5 D.3-x-6=-5x+1
6x-120
-3x-3
B
课后练习
3.方程3(x+1)-2(x-1)=1变形正确的是( )
A.3x+3-2x+2=1 B.3x+3-2x-2=1
C.3x+3+2x-2=1 D.3x+3-2x+1=1
A
B
5.方程2(x-1)=x+2的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
6.方程2(x-2)-3(4x-1)=9的解是( )
A.x=0.8 B.x=-1
C.x=-1.6 D.x=1
D
B
A
8.解方程:
(1)5(x+2)=2(5x-1);
(2)2(x-1)-(x+2)=3(4-x);
解:x=4
(3)2(3x-2)=5(x-2);
解:x=-6
(4)5(x+8)=6(2x-7)+5.
解:x=11
9.已知方程2(x-1)+1=x的解与关于x的方程3(x+m)=m-1的解相同,求m的值.
解:解方程2(x-1)+1=x得x=1,把x=1代入方程3(x+m)=m-1中得m=-2
10.某城市出租车的收费标准是:起步价7元(即行驶距离不超过3千米,都需付7元车费),超过3千米后,每增加1千米收费2.4元,不足1千米按1千米计,某人乘这种出租车从甲地到乙地刚好付19元车费,求甲、乙两地的距离?
解:设甲、乙两地的距离为x千米,根据题意,得7+2.4(x-3)=19,解得x=8,答:甲、乙两地的距离是8千米
10.解下列方程:
(1)3x-4=5-6x;
解:x=1
(2)7x+1.37=15x-0.23;
解:x=0.2
(3)4x+5=3x+3-2x;
(4)8x+16=52-4x.
解:x=3
11.解方程x-2(x-1)=4,去括号正确的是( )
A.x-2x-1=4 B.x-2x+2=4
C.x-2x-2=4 D.x-2x+1=4
12.方程4(a-x)-4(x+1)=60的解是x=1,则a的值为( )
A.-14 B.20 C.18 D.-16
B
C
13.如果a=3,那么a(x+1)=2(x+1)的解是( )
A.0 B.-1 C.无解 D.1
B
14.解下列方程:
(1)6y=2(1+y)-3(y+3);
解:y=-1
(2)2(m-3)-5(2m-1)=3(2m+1)-8;
(3)3(x-7)-2[9-4(2-x)]=22.
解:x=-9
15.已知方程2(x-1)=3(x+2)的解是m-5,求关于x的方程2[3(x-m)-4(x+1)]=3(m-2)的解.
17.若关于x的方程5x-a=4x+3的解比关于x的方程2(2x+a)+5=3(x+2)的解大8,求a的值.
解:解方程5x-a=4x+3得x=a+3,解方程2(2x+a)+5=3(x+2)得x=1-2a,因为方程5x-a=4x+3的解比方程2(2x+a)+5=3(x+2)的解大8,所以(a+3)-(1-2a)=8,解得a=2
18.(2019·海南模拟)海南五月瓜果飘香.某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
解:设李叔叔购买无核荔枝x千克,依题意得26x+22(30-x)=708.解得x=12,30-x=18.答:李叔叔购买这两种水果各12千克和18千克
19.在五一期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?说明理由.
解:(1)设一共去了x个成人,依题意得35x+0.5×35×(12-x)=350,解得x=8,12-x=4,答:他们一共去了8个成人,4个学生 (2)35×16×0.6=336(元),因为336<350,所以购买团体票更加省钱
再
见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
