湖南省衡阳市2020-2021学年高一下学期期末考试数学试题 Word版含答案解析
文档属性
| 名称 | 湖南省衡阳市2020-2021学年高一下学期期末考试数学试题 Word版含答案解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览




文档简介
衡阳市2020-2021学年高一下学期期末考试
数学试卷
注意事项:本试卷满分150分,时量为120分钟
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1. 已知集合false,false,则false( )
A. false B. false C. false D. false
2. 已知复数false满足false,则false的共轭复数false( )
A. false B. false C. false D. false
3. 设false,false是非零向量,则“存在实数false,使得false”是“false”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4. 已知空间四点false,false,false,false共面,则false的值为( )
A. 4 B. 1 C. 10 D. 11
5. 若false,则false( )
A. false B. false C. false D. false
6. 已知正数false,false满足false,且false恒成立,则false的最大值为( )
A. false B. false C. 2 D. 4
7. 新高考综合改革实施方案将采用“false”模式,“3”为语文、数学、英语所有学生必考;“1”为必须在物理、历史中选一科;“2”为再选科目,考生须在化学、生物、政治、地理4个科目中任选两科.若不考虑主观因素的影响,选择各科是等可能的,则某同学选择含有地理学科组合的概率为( )
A. false B. false C. false D. false
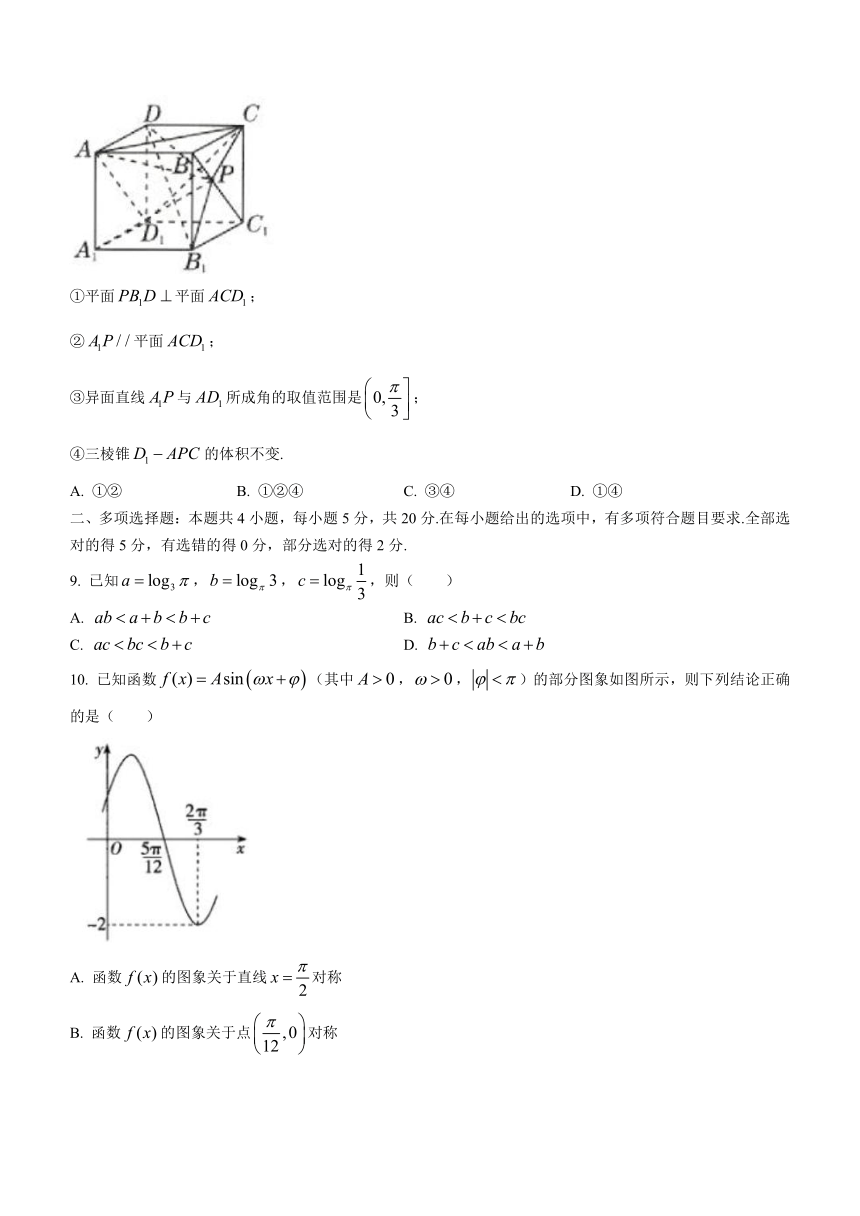
8. 如图,在正方体false中,点false在线段false上运动,则下列判断中正确的是( )
①平面false平面false;
②false平面false;
③异面直线false与false所成角的取值范围是false;
④三棱锥false的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知false,false,false,则( )
A. false B. false
C. false D. false
10. 已知函数false(其中false,false,false)的部分图象如图所示,则下列结论正确的是( )
A. 函数false的图象关于直线false对称
B. 函数false的图象关于点false对称
C. 函数false在区间false上单调递增
D. 函数false与false,false的图象的所有交点的横坐标之和为false
11. 4支足球队进行单循环比赛(任两支球队恰进行一场比赛,每场比赛都能分出胜负),任两支球队之间胜率都是false.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.下列结论中正确的是( )
A. 恰有四支球队并列第一名为不可能事件 B. 有可能出现恰有三支球队并列第一名
C. 恰有两支球队并列第一名的概率为false D. 只有一支球队名列第一名的概率为false
12. 《数书九章》是南宋时期杰出数学家秦九韶的著作,全书十八卷,共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九韶的许多创造性成就,其中在卷五“三斜求积术”中提出了已知三角形三边false,false,false,求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以少广求之,以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂减上,余四约之,为实;一为从隅,开平方得积.”若把以上这段文字写成公式,即false.现有false满足false,且false的面积false,请运用上述公式判断下列结论正确的是( )
A. false的周长为false B. false三个内角false,false,false满足false
C. false外接圆的直径为false D. false的中线false的长为false
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知false,false,false,则false与false的夹角为__________.
14. 一组数据按从小到大的顺序排列为1,2,2,false,5,10,其中false,已知该组数据的中位数是众数的false倍,则该组数据的标准差为___________.
15. “无字证明”就是将数学命题用简单、有创意而且易于理解的几何图形来呈现请利用甲、乙、丙的面积关系,写出该图所验证的一个三角恒等变换公式:__________.
16. 阿基米德是古希腊的一位著名的数学家,有一种空间几何体便以他的名字命名为“阿基米德立体”.“阿基米德立体”是一种高度对称的“半正多面体”(如图),并且都是可以从正多面体经过截角、截半、截边等操作构造而成,它的所有顶点都是正多面体各棱的中点,且它的三个视图全都一样.现将一个棱长为false的正方体木块加工成一个“阿基米德立体”工艺品,则所得的“阿基米德立体”工艺品共有____________个面,其表面积为___________false.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在①false,false,且false,②false,③false这三个条件中任选一个补充在下面问题中,并解答.
已知false中,三个内角false,false,false所对的边分别是false,false,false,__________.
(1)求false的值;
(2)若false,false的面积是false,点false是false的中点,求false的长度.
18. 已知函数false,函数false的图像与函数false的图像关于false轴对称.
(1)求函数false的解析式;
(2)若存在false,使等式false成立,求实数false的取值范围.
19. 如图,在四棱锥false中,底面false为平行四边形,false为等边三角形,平面false平面false,false,false,false.
(1)设false,false分别为false,false的中点,求证:false平面false;
(2)求证:false平面false;
(3)求直线false与平面false所成角的正弦值.
20. 甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为false.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
21. 为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程.非一户一表用户电费采用“合表电价”收费标准:0.65元/度.“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档
第二档
第三档
每户每月用电量(单位:度)
false
false
false
电价(单位:元/度)
0.61
0.66
0.91
例如:某用户11月用电410度,采用合表电价收费标准应交电费false元,若采用阶梯电价收费标准,应交电费false元.
为调查阶梯电价是否能取到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量(单位:度)为:88,268,370,140,440,420,520,320,230,380.
组别
月用电量
频数统计
频数
频率
①
false
②
false
③
false
④
false
⑤
false
⑥
false
合计
(1)完成频率分布表,并绘制频率分布直方图:
(2)根据已有信息,试估计全市住户11月的平均用电量(同一组数据用该区间的中点值作代表);
(3)设某用户11月用电量为false度,按照合表电价收费标准应交false元,按照阶梯电价收费标准应交false元,请用false表示false和false,并求当false时,false的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于false的用户带来实惠?
22. 若函数false在false时,函数值false的取值区间恰为false,就称区间false为false的一个“倒域区间”.定义在false上的奇函数false,当false时,false.
(1)求false的解析式;
(2)求函数false在false内的“倒域区间”;
(3)若函数false在定义域内所有“倒域区间”上的图像作为函数false的图像,是否存在实数false,使集合false恰含有2个元素?若存在,求出false的值;若不存在,请说明理由.
衡阳市2020-2021学年高一下学期期末考试数学参考答案
1.答案:B
解析:false,
false.
故选B.
2.答案:A
解析:false
false
则false,答案:A
【点睛】本题考查复数的运算,关键在于分母的实数化和共轭复数的使用,属于简单题.
3.答案:B
解析:存在实数false,使得false,
说明向量false共线,当false同向时,false成立,
当false反向时,false不成立,所以,充分性不成立.
当false成立时,有false同向,存在实数false,使得false成立,必要性成立,
即“存在实数false,使得false”是“false”的必要而不充分条件.
故选B.
4.答案:D
解析:依题意,得false.false四点共面,false共面,false存在实数false,使得false,即false,false解得false
5.答案:C
解析:本题考查三角函数的化简与计算.因为false,所以falsefalsefalse.
6.答案:B
解析:因为正数x,y满足false,
所以false.
因为false
false,
当且仅当false时等号成立,
所以false,即false的最小值为false.
若false恒成立,则m的最大值为false.故选B.
7.答案:B
解析:按照“false”模式选科具体组合如下:
(物理,化学,生物)、(物理,化学,地理)、(物理,化学,政治)、(物理,生物,政治)、(物理,生物,地理)、(物理,政治,地理)、(历史,化学,生物)、(历史,化学,地理)、(历史,化学,政治)、(历史,生物,政治)、(历史,生物,地理)、(历史,政治,地理),共12种组合,其中含地理学科的组合有6种,所以某同学选择含地理学科组合的概率false,故选B.
8.答案:B
解析:对于①,如图,连接false,根据正方体的性质,有false平面false平面false,从而可以证明 平面false平面false,正确.
②如图,连接false容易证 明平面false平面false,从而由线面平行的定义可得false平面false,正确.
③当false与线段false的两端点重合时,false与false所成角取最小值false,当false与线段false的中点重合时,false与false所成角取最大值false,故false与false所成角的范围是false,错误.
④false,false到平面false的距离不变,且三角形false的面积不变,∴三棱锥false的体积不变,正确.
正确的命题为①②④.故选B.
9.答案:CD
解析:因为false,又false所以false
所以C正确,B错误.因为false,所以D正确,A错误.
10.答案:CD
解析:由题图可得,false,false,故false,则false,
所以false.
又因为false,
所以false,
所以false.
又false,所以false,所以false.
当false时,false,此时false,所以false的图象不关于点false,故B中结论不正确.
令false,可得false,即函数的一个单调递增区间为false,故C中结论正确.
令false,则false,false或false,false,即false,false或false,false.
所以满足false的交点的横坐标有0,false,false,false和为false,故D中结论正确.
故选CD.
11.答案:ABD
解析:4支足球队进行单循环比赛总的比赛共有false场比赛,比赛的所有结果共有false种;
选项A,这6场比赛中若4支球队优先各赢一场,则还有2场必然有2支或1支队伍获胜,那么所得分值不可能都一样,故是不可能事件,正确;
选项B,其中false6场比赛中,依次获胜的可以是false,此时3队都获得2分,并列第一名,正确;
选项C,在false6场比赛中,从中选2支球队并列第一名有false种可能,若选中false,其中第一类false赢false,有false和false两种情况,同理第二类false赢false,也有两种,故恰有两支球队并列第一名的概率为false,错误;
选项D,从4支球队中选一支为第一名有4种可能;这一支球队比赛的3场应都赢,则另外3场的可能有false种,故只有一支球队名列第一名的概率为false,正确.
故选:ABD.
12.答案:ABC
解析:由正弦定理可得false.设false,解得false的周长为false,故A正确;由余弦定理得false,故B正确;由正弦定理知,false外接圆的直径false,故C正确;由中线定理得false,即false,false,故D错误.故选ABC.
13.答案:false
解析:
14.答案:3
解析:由题意,可得该组数据的众数为2,所以false,解得false,故该组数据的平均数为false.所以该组数据的方差为false,即标准差为3.
15.答案:false
解析:由三角形的面积公式,得甲的面积为false,乙的面积为false,丙的面积为false,故false,即false.
16.答案:14;false
解析:
17.答案:选①:由false,得false,
得false,得false,
又false,false,所以false,
又false,所以false.
②因为false,
根据正弦定理得false,
所以false,
所以false,
所以false.
因为false,所以false,
又false,所以false.
③因为false,
所以false,
所以false.
因为false,false,所以false,所以false,
又false,所以false.
(2)在false中,由false,false,得false.
由false的面积为false,得false,所以false.
因为M是false的中点,所以false,
从而false,
所以false.
18.答案:(1)易得falsefalse.
因为函数false的图像与函数false的图像关于y轴对称,
所以false,所以false.
(2)令false.
由false,可得false,则false,
所以关于t的方程false在false上有解,
故关于t的方程false在false上有解,
又函数false的值域为false,
所以false,故实数m的取值范围为false.
解析:
19.答案:(1)如图,连接BD,易知false,false.
又false,故false.
又false平面PAD,false平面PAD,所以false平面PAD.
(2)如图,取棱PC的中点N,连接DN.
依题意,得false.
又平面false平面PCD,平面false平面false,
所以false平面PAC.
又false平面PAC,故false.
又false,false,所以false平面PCD.
(3)如图,连接AN.
由(2)中false平面PAC,可知false为直线AD与平面PAC所成的角.
因为false为等边三角形,false且N为PC的中点,
所以false.
又false,在false中,false,
所以直线AD与平面PAC所成角的正弦值为false.
解析:
20.答案:(1)甲连胜四场的概率为false.
(2)根据赛制,至少需要进行四场比赛,至多需要进行五场比赛.
比赛四场结束,共有三种情况:
乙连胜四场的概率为false;
丙上场后连胜三场的概率为false.
所以需要进行第五场比赛的概率为false.
(3)丙最终获胜,有两种情况:
比赛四场结束且丙最终获胜的概率为false;
比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜、负、轮空结果有三种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为false.
因此丙最终获胜的概率为false.
解析:
21.答案:(1)频率分布表如下:
组别
月用电量
频数
频率
①
false
4
0.04
②
false
12
0.12
③
false
24
0.24
④
false
30
0.3
⑤
false
26
0.26
⑥
false
4
0.04
合计
100
1
频率分布直方图如下:
(2)该100户用户11月的平均用电量:
false度,
所以估计全市住户11月的平均用电量为324度.
(3)false,
false
由false,得false或false
或false
解得false,
因为false,所以x的最大值为423.
根据频率分布直方图,false时的频率为:
false,
故估计“阶梯电价”能给不低于false的用户带来实惠.
22. 解析:
(1)当false时,false.
false.
(2)设false,∵false在false上递减,
∴false整理得
false,解得false.
∴false在false内的“倒域区间”为false.
(3)∵false在false时,函数值false的取值区间恰为false,其中false,false,
∴false,∴false、false同号.只考虑false或false,
当false时,根据false的图像知,false最大值为1,false,false,
∴false,由(Ⅱ)知false在false内的“倒域区间”为false;
当false,false最小值为-1,false,false,
∴false,同理知false在false内的“倒域区间”为false.
false.
?依题意:抛物线与函数false的图象有两个交点时,一个交点在第一象限,一个交点在第三象限.
因此,false应当使方程false,在false内恰有一个实数根
并且使方程false,在false内恰有一个实数.
由方程false在false内恰有一根知false;
由方程false在false内恰有一根知false,
综上:false.
数学试卷
注意事项:本试卷满分150分,时量为120分钟
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1. 已知集合false,false,则false( )
A. false B. false C. false D. false
2. 已知复数false满足false,则false的共轭复数false( )
A. false B. false C. false D. false
3. 设false,false是非零向量,则“存在实数false,使得false”是“false”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4. 已知空间四点false,false,false,false共面,则false的值为( )
A. 4 B. 1 C. 10 D. 11
5. 若false,则false( )
A. false B. false C. false D. false
6. 已知正数false,false满足false,且false恒成立,则false的最大值为( )
A. false B. false C. 2 D. 4
7. 新高考综合改革实施方案将采用“false”模式,“3”为语文、数学、英语所有学生必考;“1”为必须在物理、历史中选一科;“2”为再选科目,考生须在化学、生物、政治、地理4个科目中任选两科.若不考虑主观因素的影响,选择各科是等可能的,则某同学选择含有地理学科组合的概率为( )
A. false B. false C. false D. false
8. 如图,在正方体false中,点false在线段false上运动,则下列判断中正确的是( )
①平面false平面false;
②false平面false;
③异面直线false与false所成角的取值范围是false;
④三棱锥false的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知false,false,false,则( )
A. false B. false
C. false D. false
10. 已知函数false(其中false,false,false)的部分图象如图所示,则下列结论正确的是( )
A. 函数false的图象关于直线false对称
B. 函数false的图象关于点false对称
C. 函数false在区间false上单调递增
D. 函数false与false,false的图象的所有交点的横坐标之和为false
11. 4支足球队进行单循环比赛(任两支球队恰进行一场比赛,每场比赛都能分出胜负),任两支球队之间胜率都是false.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.下列结论中正确的是( )
A. 恰有四支球队并列第一名为不可能事件 B. 有可能出现恰有三支球队并列第一名
C. 恰有两支球队并列第一名的概率为false D. 只有一支球队名列第一名的概率为false
12. 《数书九章》是南宋时期杰出数学家秦九韶的著作,全书十八卷,共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九韶的许多创造性成就,其中在卷五“三斜求积术”中提出了已知三角形三边false,false,false,求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以少广求之,以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂减上,余四约之,为实;一为从隅,开平方得积.”若把以上这段文字写成公式,即false.现有false满足false,且false的面积false,请运用上述公式判断下列结论正确的是( )
A. false的周长为false B. false三个内角false,false,false满足false
C. false外接圆的直径为false D. false的中线false的长为false
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知false,false,false,则false与false的夹角为__________.
14. 一组数据按从小到大的顺序排列为1,2,2,false,5,10,其中false,已知该组数据的中位数是众数的false倍,则该组数据的标准差为___________.
15. “无字证明”就是将数学命题用简单、有创意而且易于理解的几何图形来呈现请利用甲、乙、丙的面积关系,写出该图所验证的一个三角恒等变换公式:__________.
16. 阿基米德是古希腊的一位著名的数学家,有一种空间几何体便以他的名字命名为“阿基米德立体”.“阿基米德立体”是一种高度对称的“半正多面体”(如图),并且都是可以从正多面体经过截角、截半、截边等操作构造而成,它的所有顶点都是正多面体各棱的中点,且它的三个视图全都一样.现将一个棱长为false的正方体木块加工成一个“阿基米德立体”工艺品,则所得的“阿基米德立体”工艺品共有____________个面,其表面积为___________false.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在①false,false,且false,②false,③false这三个条件中任选一个补充在下面问题中,并解答.
已知false中,三个内角false,false,false所对的边分别是false,false,false,__________.
(1)求false的值;
(2)若false,false的面积是false,点false是false的中点,求false的长度.
18. 已知函数false,函数false的图像与函数false的图像关于false轴对称.
(1)求函数false的解析式;
(2)若存在false,使等式false成立,求实数false的取值范围.
19. 如图,在四棱锥false中,底面false为平行四边形,false为等边三角形,平面false平面false,false,false,false.
(1)设false,false分别为false,false的中点,求证:false平面false;
(2)求证:false平面false;
(3)求直线false与平面false所成角的正弦值.
20. 甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为false.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
21. 为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程.非一户一表用户电费采用“合表电价”收费标准:0.65元/度.“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档
第二档
第三档
每户每月用电量(单位:度)
false
false
false
电价(单位:元/度)
0.61
0.66
0.91
例如:某用户11月用电410度,采用合表电价收费标准应交电费false元,若采用阶梯电价收费标准,应交电费false元.
为调查阶梯电价是否能取到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量(单位:度)为:88,268,370,140,440,420,520,320,230,380.
组别
月用电量
频数统计
频数
频率
①
false
②
false
③
false
④
false
⑤
false
⑥
false
合计
(1)完成频率分布表,并绘制频率分布直方图:
(2)根据已有信息,试估计全市住户11月的平均用电量(同一组数据用该区间的中点值作代表);
(3)设某用户11月用电量为false度,按照合表电价收费标准应交false元,按照阶梯电价收费标准应交false元,请用false表示false和false,并求当false时,false的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于false的用户带来实惠?
22. 若函数false在false时,函数值false的取值区间恰为false,就称区间false为false的一个“倒域区间”.定义在false上的奇函数false,当false时,false.
(1)求false的解析式;
(2)求函数false在false内的“倒域区间”;
(3)若函数false在定义域内所有“倒域区间”上的图像作为函数false的图像,是否存在实数false,使集合false恰含有2个元素?若存在,求出false的值;若不存在,请说明理由.
衡阳市2020-2021学年高一下学期期末考试数学参考答案
1.答案:B
解析:false,
false.
故选B.
2.答案:A
解析:false
false
则false,答案:A
【点睛】本题考查复数的运算,关键在于分母的实数化和共轭复数的使用,属于简单题.
3.答案:B
解析:存在实数false,使得false,
说明向量false共线,当false同向时,false成立,
当false反向时,false不成立,所以,充分性不成立.
当false成立时,有false同向,存在实数false,使得false成立,必要性成立,
即“存在实数false,使得false”是“false”的必要而不充分条件.
故选B.
4.答案:D
解析:依题意,得false.false四点共面,false共面,false存在实数false,使得false,即false,false解得false
5.答案:C
解析:本题考查三角函数的化简与计算.因为false,所以falsefalsefalse.
6.答案:B
解析:因为正数x,y满足false,
所以false.
因为false
false,
当且仅当false时等号成立,
所以false,即false的最小值为false.
若false恒成立,则m的最大值为false.故选B.
7.答案:B
解析:按照“false”模式选科具体组合如下:
(物理,化学,生物)、(物理,化学,地理)、(物理,化学,政治)、(物理,生物,政治)、(物理,生物,地理)、(物理,政治,地理)、(历史,化学,生物)、(历史,化学,地理)、(历史,化学,政治)、(历史,生物,政治)、(历史,生物,地理)、(历史,政治,地理),共12种组合,其中含地理学科的组合有6种,所以某同学选择含地理学科组合的概率false,故选B.
8.答案:B
解析:对于①,如图,连接false,根据正方体的性质,有false平面false平面false,从而可以证明 平面false平面false,正确.
②如图,连接false容易证 明平面false平面false,从而由线面平行的定义可得false平面false,正确.
③当false与线段false的两端点重合时,false与false所成角取最小值false,当false与线段false的中点重合时,false与false所成角取最大值false,故false与false所成角的范围是false,错误.
④false,false到平面false的距离不变,且三角形false的面积不变,∴三棱锥false的体积不变,正确.
正确的命题为①②④.故选B.
9.答案:CD
解析:因为false,又false所以false
所以C正确,B错误.因为false,所以D正确,A错误.
10.答案:CD
解析:由题图可得,false,false,故false,则false,
所以false.
又因为false,
所以false,
所以false.
又false,所以false,所以false.
当false时,false,此时false,所以false的图象不关于点false,故B中结论不正确.
令false,可得false,即函数的一个单调递增区间为false,故C中结论正确.
令false,则false,false或false,false,即false,false或false,false.
所以满足false的交点的横坐标有0,false,false,false和为false,故D中结论正确.
故选CD.
11.答案:ABD
解析:4支足球队进行单循环比赛总的比赛共有false场比赛,比赛的所有结果共有false种;
选项A,这6场比赛中若4支球队优先各赢一场,则还有2场必然有2支或1支队伍获胜,那么所得分值不可能都一样,故是不可能事件,正确;
选项B,其中false6场比赛中,依次获胜的可以是false,此时3队都获得2分,并列第一名,正确;
选项C,在false6场比赛中,从中选2支球队并列第一名有false种可能,若选中false,其中第一类false赢false,有false和false两种情况,同理第二类false赢false,也有两种,故恰有两支球队并列第一名的概率为false,错误;
选项D,从4支球队中选一支为第一名有4种可能;这一支球队比赛的3场应都赢,则另外3场的可能有false种,故只有一支球队名列第一名的概率为false,正确.
故选:ABD.
12.答案:ABC
解析:由正弦定理可得false.设false,解得false的周长为false,故A正确;由余弦定理得false,故B正确;由正弦定理知,false外接圆的直径false,故C正确;由中线定理得false,即false,false,故D错误.故选ABC.
13.答案:false
解析:
14.答案:3
解析:由题意,可得该组数据的众数为2,所以false,解得false,故该组数据的平均数为false.所以该组数据的方差为false,即标准差为3.
15.答案:false
解析:由三角形的面积公式,得甲的面积为false,乙的面积为false,丙的面积为false,故false,即false.
16.答案:14;false
解析:
17.答案:选①:由false,得false,
得false,得false,
又false,false,所以false,
又false,所以false.
②因为false,
根据正弦定理得false,
所以false,
所以false,
所以false.
因为false,所以false,
又false,所以false.
③因为false,
所以false,
所以false.
因为false,false,所以false,所以false,
又false,所以false.
(2)在false中,由false,false,得false.
由false的面积为false,得false,所以false.
因为M是false的中点,所以false,
从而false,
所以false.
18.答案:(1)易得falsefalse.
因为函数false的图像与函数false的图像关于y轴对称,
所以false,所以false.
(2)令false.
由false,可得false,则false,
所以关于t的方程false在false上有解,
故关于t的方程false在false上有解,
又函数false的值域为false,
所以false,故实数m的取值范围为false.
解析:
19.答案:(1)如图,连接BD,易知false,false.
又false,故false.
又false平面PAD,false平面PAD,所以false平面PAD.
(2)如图,取棱PC的中点N,连接DN.
依题意,得false.
又平面false平面PCD,平面false平面false,
所以false平面PAC.
又false平面PAC,故false.
又false,false,所以false平面PCD.
(3)如图,连接AN.
由(2)中false平面PAC,可知false为直线AD与平面PAC所成的角.
因为false为等边三角形,false且N为PC的中点,
所以false.
又false,在false中,false,
所以直线AD与平面PAC所成角的正弦值为false.
解析:
20.答案:(1)甲连胜四场的概率为false.
(2)根据赛制,至少需要进行四场比赛,至多需要进行五场比赛.
比赛四场结束,共有三种情况:
乙连胜四场的概率为false;
丙上场后连胜三场的概率为false.
所以需要进行第五场比赛的概率为false.
(3)丙最终获胜,有两种情况:
比赛四场结束且丙最终获胜的概率为false;
比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜、负、轮空结果有三种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为false.
因此丙最终获胜的概率为false.
解析:
21.答案:(1)频率分布表如下:
组别
月用电量
频数
频率
①
false
4
0.04
②
false
12
0.12
③
false
24
0.24
④
false
30
0.3
⑤
false
26
0.26
⑥
false
4
0.04
合计
100
1
频率分布直方图如下:
(2)该100户用户11月的平均用电量:
false度,
所以估计全市住户11月的平均用电量为324度.
(3)false,
false
由false,得false或false
或false
解得false,
因为false,所以x的最大值为423.
根据频率分布直方图,false时的频率为:
false,
故估计“阶梯电价”能给不低于false的用户带来实惠.
22. 解析:
(1)当false时,false.
false.
(2)设false,∵false在false上递减,
∴false整理得
false,解得false.
∴false在false内的“倒域区间”为false.
(3)∵false在false时,函数值false的取值区间恰为false,其中false,false,
∴false,∴false、false同号.只考虑false或false,
当false时,根据false的图像知,false最大值为1,false,false,
∴false,由(Ⅱ)知false在false内的“倒域区间”为false;
当false,false最小值为-1,false,false,
∴false,同理知false在false内的“倒域区间”为false.
false.
?依题意:抛物线与函数false的图象有两个交点时,一个交点在第一象限,一个交点在第三象限.
因此,false应当使方程false,在false内恰有一个实数根
并且使方程false,在false内恰有一个实数.
由方程false在false内恰有一根知false;
由方程false在false内恰有一根知false,
综上:false.
同课章节目录
