七年级基础运算每日五题练习(周)(含答案)
文档属性
| 名称 | 七年级基础运算每日五题练习(周)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级数学基础运算每日小练
一、1.化简:(1);
(2)
2.先化简,再求值.
(1),其中
,
;
(2),其中
,
.
3.解方程组:
二、4.先化简,再求值:
,其中
.
5.先化简再求值:
,其中x=﹣3,y=﹣2.
6.解下列方程组.
(1)
(2)
7.在平面直角坐标系中,已知
、
,点
在
轴上,且
的面积是6.求点
的坐标.
三、8.因式分解
①
②
③
④
⑤
⑥
⑦
⑧
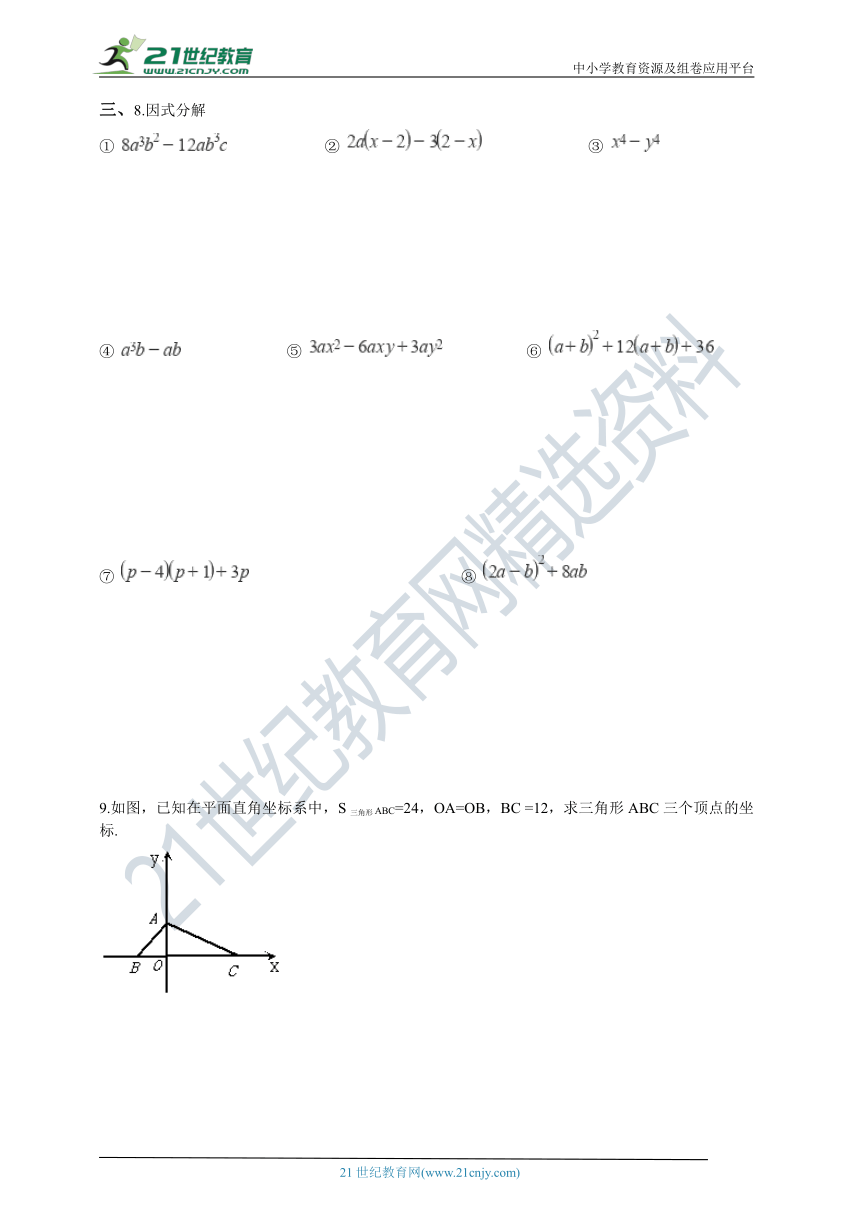
9.如图,已知在平面直角坐标系中,S三角形ABC=24,OA=OB,BC
=12,求三角形ABC三个顶点的坐标.
四、10.先化简,再求值:
,其中
a=-1,b=2
11.先化简,再求值:3a2b﹣[2ab2﹣2(﹣a2b+ab2)],其中a=﹣2,b=
.
12.解三元一次方程组:
(1)
(2).
13.写出如图中△ABC各顶点的坐标且求出此三角形的面积.
五、14.先化简,再求值:
,其中
.
15.用乘法公式计算
(1)20202﹣2019×2021.
(2)(x﹣2y+3z)(x﹣2y﹣3z).
16.计算:(1)
(2)
17.解方程组:
六、18.已知
,求
的值.
19.因式分解(1)????????????????????
???
(2)
20.先化简,再求值:
,其中
.
七、21.化简:
.
22.先化简,再求值:(
﹣
)÷
,其中a=﹣6.
23.先化简,再求值:
,其中
.
24.先化简:
,再从-1,0,1,2中选择一个适合的数代入求值.
八、第八天(共3题;共20分)
25.计算
.
26.先化简,再求值:
,其中
.
27.??(1)计算:
(2)先化简,再求值:
,请选一个你喜欢的a的值代入求值.
答案解析部分
一、第一天
1.【答案】
(1)解:
(2)解:
【解析】【分析】(1)先去括号,再合并同类项得出答案;
(2)先去括号,再合并同类项得出答案.
2.【答案】
(1)解:原式
,
,
将
,
代入得:原式
;
(2)解:原式
,
,
,
,
将
,
代入得:原式
.
【解析】【分析】(1)先去括号,再合并同类项化为最简形式,然后将a、b的值代入即可得出答案;
(2)先去括号,再合并同类项化为最简形式,然后将x、y的值代入即可得出答案.
3.【答案】
解:
解:②×3得?
6x+9y+3z=27
?④
③+④得?
11x+10z=35??
⑤
①????
⑤组成方程组
解这个方程组得
把
代入方程②得
∴原方程组的解为
【解析】【分析】运用加减消元法求出方程组即可。
二、第二天
4.【答案】
解:
=
?
将
代入得:
.
【解析】【分析】利用去括号、合并同类项将原式化简,再将x值代入计算即可.
5.【答案】
解:
当x=-3,y=-2时,原式=-(-2)2-2×(-3)+2×(-2)=-4+6-4=-2.
【解析】【分析】原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
6.【答案】
(1)解:原方程组可变形为:
①×2+②得:11x=22
解得:x=2,
把x=2代入①得:y=3
所以原方程组的解为
(2)解:
②-①得:x-
z
=-2④,
由④和③组成一个二次一次方程组
解得:
,
把
代入①得:y=-3,
所以原方程组的解是
【解析】【分析】(1)利用加减消元法求解,首先
①×2+②
消去y求出x的值,再将x的值代入①求出y的值,从而即可得出方程组的解;
(2)
②-①得出x-
z
=-2,再和③组成二元一次方程组,解出x和z得值,再把x、z的值代入①得出y的值即可.
?
7.【答案】
解:∵A(0,0)、B(3,0),
∴AB=3,且AB在x轴上,
设点C坐标是(0,y),则根据题意得,
AB×OC=6,即
×3×
=6,
解得y=±4.
∴点C坐标是:(0,4)或(0,﹣4).
【解析】【分析】
三、第三天
8.【答案】
解:①原式
;
②原式
;
③原式
;
④原式
;
⑤原式
;
⑥原式
;
⑦原式
;
⑧原式
.
【解析】【分析】(1)首先对该式提取公因式
即可解答;(2)首先对该式提取公因式
即可解答;(3)利用平方差公式进行分解即可;(4)首先提取公因式a,然后再利用平方差公式进行解答即可;(5)首先提取公因式,然后再利用完全平方公式进行解答即可;(6)利用完全平方公式进行解答即可;(7)首先对该式进行变形,然后再利用平方差公式进行解答即可;(8)利用完全平方公式进行解答即可.
9.【答案】
解:
∴OC=8,
∵点O为原点,
∴A(0,4),B(-4,0),C(8,0).
【解析】【分析】首先根据面积求得OA的长,再根据已知条件求得OB的长,最后求得OC的长.最后写坐标的时候注意点的位置.
四、第四天
10.【答案】
解:
=
=
当
a=-1,b=2时,
原式=
.
【解析】【分析】整式的加减混合运算,先去括号,然后合并同类项化简,最后代入求值即可.
11.【答案】
解:原式=3a2b﹣2ab2+2(﹣a2b+ab2)=3a2b﹣2ab2﹣2a2b+2ab2=a2b,
把a=﹣2,b=
代入上式可得:
原式=(﹣2)2×
=2.
【解析】【分析】直接去括号,进而合并同类项化为最简形式,再把a,b的值代入算出答案.
12.【答案】
(1)解:
,①+②得:5x+2y=16④,②+③得:3x+4y=18⑤,
④×2﹣⑤得:7x=14,即x=2,把x=2代入④得:y=3,
把x=2,y=3代入③得:z=1,
则方程组的解为
;
(2)解:
,②﹣③得:x+3z=5④,④﹣①得:2z=2,即z=1,
把z=1代入④得:x=2,把z=1,x=2代入③得:y=4,
则方程组的解为
.
【解析】【分析】解三元一次方程组时,利用加减消元法消去一个未知数,转化为二元一次方程组,再解出方程组的解即可。
13.【答案】
解:根据图形得:A(2,2)、B(-2,-1)、C(3,-2),
三角形的面积是
=5×4-6-2-2.5=9.5.
故答案为:A(2,2)、B(-2,-1)、C(3,-2),三角形的面积是9.5.
【解析】【分析】首先根据坐标的定义正确写出三个顶点的坐标,再根据矩形的面积减去三个直角三角形的面积进行计算.
五、第五天
14.【答案】
解:原式
??
?
?.?
当
时,
原式
.
【解析】【分析】先去小括号,然后去中括号,合并同类项进行进行化简,再将a、b、c的值代入化简的结果即可算出答案.
15.【答案】
(1)解:原式=20202﹣(2020﹣1)×(2020+1)
=20202﹣20202+1
=1;
(2)解:原式=(x﹣2y)2﹣(3z)2
=x2﹣4xy+4y2﹣9z2
.
【解析】【分析】(1)根据平方差公式计算即可;
(2)根据平方差公式和完全平方公式计算即可。
?
?
16.【答案】
(1)
=
=
(2)
=
=
=
【解析】【分析】(1)直接利用负指数幂的性质以及零指数幂的性质分别化简在进行计算,即可求出答案;
(2)先通分,再利用分式加法运算法则化简求出答案.
六、第六天
17.【答案】
解:
①+③得,
①?3+②?2,得
④与⑤组成方程组,得
解得:
把
代入①,得
解得:
原方程组的解为:
.
【解析】【分析】利用三元一次方程组的解法求解即可。
18.【答案】
解:∵
,
∴
【解析】【分析】将
代入M-3N中,去括号,再合并同类项即可.
19.【答案】
(1)解:原式=
=
=
;
(2)解:原式=
=
=
.
【解析】【分析】(1)先利用完全平方公式分解,再利用平方差公式进行第二次分解因式即可;
(2)先提取公因式xn
,
再利用平方差公式第二次分解因式即可.
20.【答案】
解:原式
当
时,原式
【解析】【分析】先将原式转化为同分母的分式相减,再利用同分母分式相减,分母不变,把分子相减。将其结果化成最简分式,然后将x的值代入计算.
七、第七天
21.【答案】
解:原式=
=
=
=
=
【解析】【分析】将括号内通分并利用同分母分式减法法则计算,再将除法转化为乘法,进行约分即可化简.
22.【答案】
解:原式
;
当a=﹣6时,代入原式=
.
【解析】【分析】先将分式化简再将
a=﹣6代入化简后的式子计算即可。
23.【答案】
解:原式
,
当
时,原式
.
【解析】【分析】根据分式的混合运算法则计算化简,然后代入x的值计算即可.
24.【答案】
解:
=
=
=
由原式可知,a不能取1,0,-1,
∴a=2时,原式=
【解析】【分析】由题意先将括号内的分式通分,再将每一个分式的分子和分母分解因式并约分,即可将分式化简,再选择一个符合题意的a的值的代入化简后的分式计算可求解.
八、第八天
25.【答案】
解:原式=
=
=
=
=
【解析】【分析】将括号里的分式通分计算,再将分式除法转化为乘法运算,然后约分化简.
26.【答案】
解:原式
将
代入得:
原式
【解析】【分析】将括号第一个分式约分,再进行同分母分式加减运算,接着进行乘法运算即可化简,最后将x值代入计算即可.
27.【答案】
(1)解:原式
=
=
(2)解:原式
=
=
=
请选一个你喜欢的a的值代入求值
(注意a不能取1,0)
【解析】【分析】⑴根据分式的乘法和除法化简即可.⑵根据分式的减法和除法化简即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
七年级数学基础运算每日小练
一、1.化简:(1);
(2)
2.先化简,再求值.
(1),其中
,
;
(2),其中
,
.
3.解方程组:
二、4.先化简,再求值:
,其中
.
5.先化简再求值:
,其中x=﹣3,y=﹣2.
6.解下列方程组.
(1)
(2)
7.在平面直角坐标系中,已知
、
,点
在
轴上,且
的面积是6.求点
的坐标.
三、8.因式分解
①
②
③
④
⑤
⑥
⑦
⑧
9.如图,已知在平面直角坐标系中,S三角形ABC=24,OA=OB,BC
=12,求三角形ABC三个顶点的坐标.
四、10.先化简,再求值:
,其中
a=-1,b=2
11.先化简,再求值:3a2b﹣[2ab2﹣2(﹣a2b+ab2)],其中a=﹣2,b=
.
12.解三元一次方程组:
(1)
(2).
13.写出如图中△ABC各顶点的坐标且求出此三角形的面积.
五、14.先化简,再求值:
,其中
.
15.用乘法公式计算
(1)20202﹣2019×2021.
(2)(x﹣2y+3z)(x﹣2y﹣3z).
16.计算:(1)
(2)
17.解方程组:
六、18.已知
,求
的值.
19.因式分解(1)????????????????????
???
(2)
20.先化简,再求值:
,其中
.
七、21.化简:
.
22.先化简,再求值:(
﹣
)÷
,其中a=﹣6.
23.先化简,再求值:
,其中
.
24.先化简:
,再从-1,0,1,2中选择一个适合的数代入求值.
八、第八天(共3题;共20分)
25.计算
.
26.先化简,再求值:
,其中
.
27.??(1)计算:
(2)先化简,再求值:
,请选一个你喜欢的a的值代入求值.
答案解析部分
一、第一天
1.【答案】
(1)解:
(2)解:
【解析】【分析】(1)先去括号,再合并同类项得出答案;
(2)先去括号,再合并同类项得出答案.
2.【答案】
(1)解:原式
,
,
将
,
代入得:原式
;
(2)解:原式
,
,
,
,
将
,
代入得:原式
.
【解析】【分析】(1)先去括号,再合并同类项化为最简形式,然后将a、b的值代入即可得出答案;
(2)先去括号,再合并同类项化为最简形式,然后将x、y的值代入即可得出答案.
3.【答案】
解:
解:②×3得?
6x+9y+3z=27
?④
③+④得?
11x+10z=35??
⑤
①????
⑤组成方程组
解这个方程组得
把
代入方程②得
∴原方程组的解为
【解析】【分析】运用加减消元法求出方程组即可。
二、第二天
4.【答案】
解:
=
?
将
代入得:
.
【解析】【分析】利用去括号、合并同类项将原式化简,再将x值代入计算即可.
5.【答案】
解:
当x=-3,y=-2时,原式=-(-2)2-2×(-3)+2×(-2)=-4+6-4=-2.
【解析】【分析】原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
6.【答案】
(1)解:原方程组可变形为:
①×2+②得:11x=22
解得:x=2,
把x=2代入①得:y=3
所以原方程组的解为
(2)解:
②-①得:x-
z
=-2④,
由④和③组成一个二次一次方程组
解得:
,
把
代入①得:y=-3,
所以原方程组的解是
【解析】【分析】(1)利用加减消元法求解,首先
①×2+②
消去y求出x的值,再将x的值代入①求出y的值,从而即可得出方程组的解;
(2)
②-①得出x-
z
=-2,再和③组成二元一次方程组,解出x和z得值,再把x、z的值代入①得出y的值即可.
?
7.【答案】
解:∵A(0,0)、B(3,0),
∴AB=3,且AB在x轴上,
设点C坐标是(0,y),则根据题意得,
AB×OC=6,即
×3×
=6,
解得y=±4.
∴点C坐标是:(0,4)或(0,﹣4).
【解析】【分析】
三、第三天
8.【答案】
解:①原式
;
②原式
;
③原式
;
④原式
;
⑤原式
;
⑥原式
;
⑦原式
;
⑧原式
.
【解析】【分析】(1)首先对该式提取公因式
即可解答;(2)首先对该式提取公因式
即可解答;(3)利用平方差公式进行分解即可;(4)首先提取公因式a,然后再利用平方差公式进行解答即可;(5)首先提取公因式,然后再利用完全平方公式进行解答即可;(6)利用完全平方公式进行解答即可;(7)首先对该式进行变形,然后再利用平方差公式进行解答即可;(8)利用完全平方公式进行解答即可.
9.【答案】
解:
∴OC=8,
∵点O为原点,
∴A(0,4),B(-4,0),C(8,0).
【解析】【分析】首先根据面积求得OA的长,再根据已知条件求得OB的长,最后求得OC的长.最后写坐标的时候注意点的位置.
四、第四天
10.【答案】
解:
=
=
当
a=-1,b=2时,
原式=
.
【解析】【分析】整式的加减混合运算,先去括号,然后合并同类项化简,最后代入求值即可.
11.【答案】
解:原式=3a2b﹣2ab2+2(﹣a2b+ab2)=3a2b﹣2ab2﹣2a2b+2ab2=a2b,
把a=﹣2,b=
代入上式可得:
原式=(﹣2)2×
=2.
【解析】【分析】直接去括号,进而合并同类项化为最简形式,再把a,b的值代入算出答案.
12.【答案】
(1)解:
,①+②得:5x+2y=16④,②+③得:3x+4y=18⑤,
④×2﹣⑤得:7x=14,即x=2,把x=2代入④得:y=3,
把x=2,y=3代入③得:z=1,
则方程组的解为
;
(2)解:
,②﹣③得:x+3z=5④,④﹣①得:2z=2,即z=1,
把z=1代入④得:x=2,把z=1,x=2代入③得:y=4,
则方程组的解为
.
【解析】【分析】解三元一次方程组时,利用加减消元法消去一个未知数,转化为二元一次方程组,再解出方程组的解即可。
13.【答案】
解:根据图形得:A(2,2)、B(-2,-1)、C(3,-2),
三角形的面积是
=5×4-6-2-2.5=9.5.
故答案为:A(2,2)、B(-2,-1)、C(3,-2),三角形的面积是9.5.
【解析】【分析】首先根据坐标的定义正确写出三个顶点的坐标,再根据矩形的面积减去三个直角三角形的面积进行计算.
五、第五天
14.【答案】
解:原式
??
?
?.?
当
时,
原式
.
【解析】【分析】先去小括号,然后去中括号,合并同类项进行进行化简,再将a、b、c的值代入化简的结果即可算出答案.
15.【答案】
(1)解:原式=20202﹣(2020﹣1)×(2020+1)
=20202﹣20202+1
=1;
(2)解:原式=(x﹣2y)2﹣(3z)2
=x2﹣4xy+4y2﹣9z2
.
【解析】【分析】(1)根据平方差公式计算即可;
(2)根据平方差公式和完全平方公式计算即可。
?
?
16.【答案】
(1)
=
=
(2)
=
=
=
【解析】【分析】(1)直接利用负指数幂的性质以及零指数幂的性质分别化简在进行计算,即可求出答案;
(2)先通分,再利用分式加法运算法则化简求出答案.
六、第六天
17.【答案】
解:
①+③得,
①?3+②?2,得
④与⑤组成方程组,得
解得:
把
代入①,得
解得:
原方程组的解为:
.
【解析】【分析】利用三元一次方程组的解法求解即可。
18.【答案】
解:∵
,
∴
【解析】【分析】将
代入M-3N中,去括号,再合并同类项即可.
19.【答案】
(1)解:原式=
=
=
;
(2)解:原式=
=
=
.
【解析】【分析】(1)先利用完全平方公式分解,再利用平方差公式进行第二次分解因式即可;
(2)先提取公因式xn
,
再利用平方差公式第二次分解因式即可.
20.【答案】
解:原式
当
时,原式
【解析】【分析】先将原式转化为同分母的分式相减,再利用同分母分式相减,分母不变,把分子相减。将其结果化成最简分式,然后将x的值代入计算.
七、第七天
21.【答案】
解:原式=
=
=
=
=
【解析】【分析】将括号内通分并利用同分母分式减法法则计算,再将除法转化为乘法,进行约分即可化简.
22.【答案】
解:原式
;
当a=﹣6时,代入原式=
.
【解析】【分析】先将分式化简再将
a=﹣6代入化简后的式子计算即可。
23.【答案】
解:原式
,
当
时,原式
.
【解析】【分析】根据分式的混合运算法则计算化简,然后代入x的值计算即可.
24.【答案】
解:
=
=
=
由原式可知,a不能取1,0,-1,
∴a=2时,原式=
【解析】【分析】由题意先将括号内的分式通分,再将每一个分式的分子和分母分解因式并约分,即可将分式化简,再选择一个符合题意的a的值的代入化简后的分式计算可求解.
八、第八天
25.【答案】
解:原式=
=
=
=
=
【解析】【分析】将括号里的分式通分计算,再将分式除法转化为乘法运算,然后约分化简.
26.【答案】
解:原式
将
代入得:
原式
【解析】【分析】将括号第一个分式约分,再进行同分母分式加减运算,接着进行乘法运算即可化简,最后将x值代入计算即可.
27.【答案】
(1)解:原式
=
=
(2)解:原式
=
=
=
请选一个你喜欢的a的值代入求值
(注意a不能取1,0)
【解析】【分析】⑴根据分式的乘法和除法化简即可.⑵根据分式的减法和除法化简即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
