重庆第八高级中学校2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 重庆第八高级中学校2020-2021学年高一下学期期末考试数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 923.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览



文档简介
重庆八中2020—2021学年度(下)期末考试高一年级
数学试题
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 直线的倾斜角是( )
A. B. C. D.
2. 复数(为虚数单位)的虚部为( )
A. B. C. D.
3. 在中,内角,,的对边分别为,,,若,,,则角为( )
A. 30° B. 30°或150° C. 60° D. 60°或120°
4. 已知,为两条不同的直线,,为两个不同的平面,则下列说法正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
5. 直线与圆交于、两点,则( )
A. 2 B. C. 6 D.
6. 已知与是直线(为常数)上两个不同的点,则关于和的交点情况是( )
A. 无论,,如何,总有唯一交点 B. 存在,,使之有无穷多个交点
C. 无论,,如何,总是无交点 D. 存在,,使之无交点
7. 如图,在正三棱柱中,,则直线与所成角的余弦值为( )
A. B. C. D.
8. 已知点为直线上的一个动点,过点作圆的两条切线,切点分别为,,则四边形面积的最小值为( )
A. B. C. D.
二.选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分.)
9. 复数的共轭复数记为,则下列运算结果一定是实数的是( )
A. B. C. D.
10. 如果,,那么直线经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
11. 在菱形中,,,,分别为,的中点,则( )
A. B.
C. 在方向上的投影向量的模为2 D.
12. 在正方体中,点在线段上运动,下列说法正确的是( )
A. 平面平面 B. 平面
C. 异面直线与所成角的取值范围是 D. 三棱锥的体积不变
三.填空题(本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上.)
13. 若直线与垂直,则实数______.
14. 已知圆与圆相交于,两点,则直线的方程为______.
15. 己知复数,满足,,若(为虚数单位),则______.
16. 已知圆锥的母线长为2,轴截面是过该圆锥顶点的所有截面中面积最大的一个,则该圆锥的表面积的最大值为______.
四.解答题(本大题共6小题,共70分.请将正确答案做在答题卷相应位置,要有必要的推理或证明过程.)
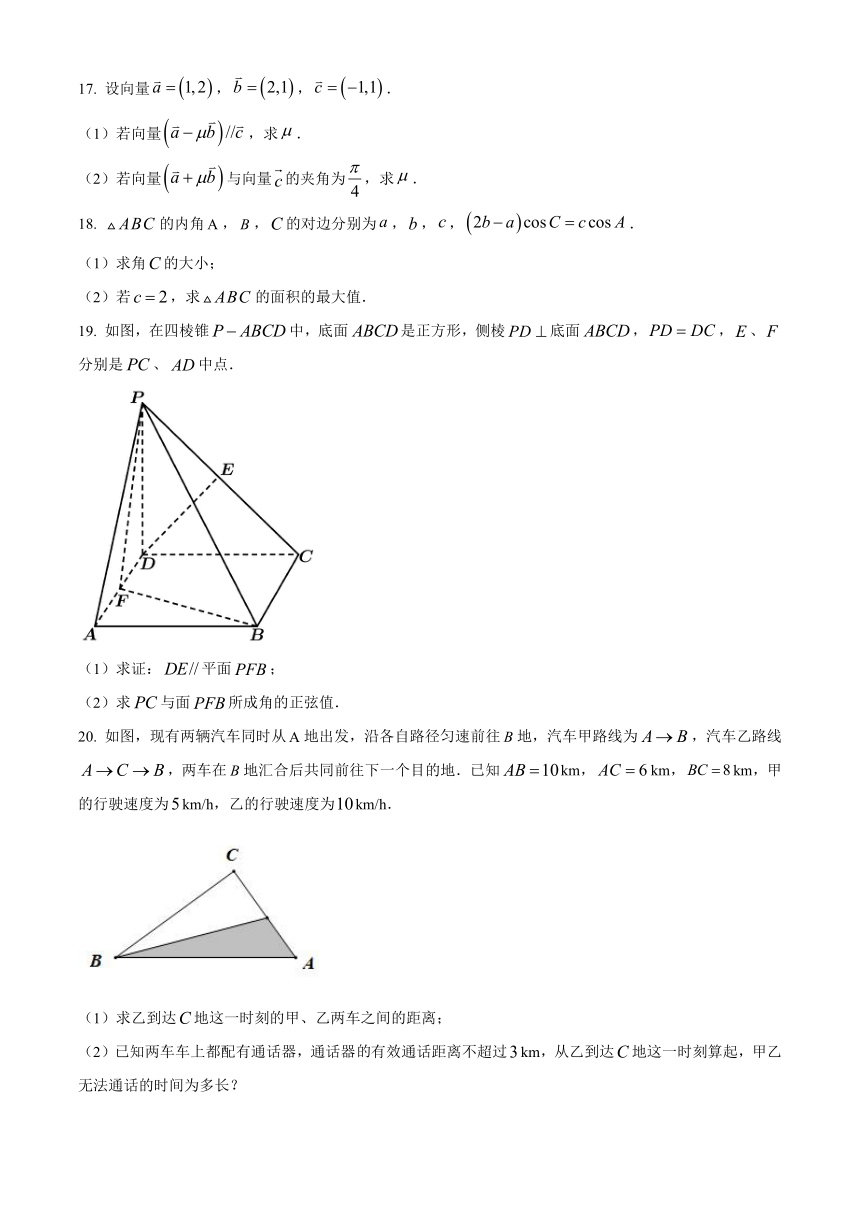
17. 设向量,,.
(1)若向量,求.
(2)若向量与向量的夹角为,求.
18. 的内角,,的对边分别为,,,.
(1)求角的大小;
(2)若,求的面积的最大值.
19. 如图,在四棱锥中,底面是正方形,侧棱底面,,、分别是、中点.
(1)求证:平面;
(2)求与面所成角的正弦值.
20. 如图,现有两辆汽车同时从地出发,沿各自路径匀速前往地,汽车甲路线为,汽车乙路线,两车在地汇合后共同前往下一个目的地.已知km,km,km,甲的行驶速度为km/h,乙的行驶速度为km/h.
(1)求乙到达地这一时刻的甲、乙两车之间的距离;
(2)已知两车车上都配有通话器,通话器有效通话距离不超过km,从乙到达地这一时刻算起,甲乙无法通话的时间为多长?
21. 如图,已知在三棱柱中,四边形为正方形,,,、分别是、的中点,点是线段上的动点.
(1)证明:;
(2)若,若,求平面与平面所成锐二面角余弦值.
22. 已知圆心在第一象限,半径为的圆与轴相切,且与轴正半轴交于,两点(在左侧),(为坐标原点).
(1)求圆的标准方程;
(2)过点任作一条直线与圆相交于,两点.
①证明:为定值;②求的最小值.
重庆八中2020—2021学年度(下)期末考试高一年级
数学试题 答案版
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 直线的倾斜角是( )
A. B. C. D.
【答案】D
2. 复数(为虚数单位)的虚部为( )
A. B. C. D.
【答案】C
3. 在中,内角,,的对边分别为,,,若,,,则角为( )
A. 30° B. 30°或150° C. 60° D. 60°或120°
【答案】A
4. 已知,为两条不同的直线,,为两个不同的平面,则下列说法正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
【答案】D
5. 直线与圆交于、两点,则( )
A. 2 B. C. 6 D.
【答案】B
6. 已知与是直线(为常数)上两个不同的点,则关于和的交点情况是( )
A. 无论,,如何,总有唯一交点 B. 存在,,使之有无穷多个交点
C. 无论,,如何,总是无交点 D. 存在,,使之无交点
【答案】A
7. 如图,在正三棱柱中,,则直线与所成角的余弦值为( )
A. B. C. D.
【答案】D
8. 已知点为直线上的一个动点,过点作圆的两条切线,切点分别为,,则四边形面积的最小值为( )
A. B. C. D.
【答案】C
二.选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分.)
9. 复数的共轭复数记为,则下列运算结果一定是实数的是( )
A. B. C. D.
【答案】AC
10. 如果,,那么直线经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】ACD
11. 在菱形中,,,,分别为,的中点,则( )
A. B.
C. 在方向上的投影向量的模为2 D.
【答案】ACD
12. 在正方体中,点在线段上运动,下列说法正确的是( )
A. 平面平面 B. 平面
C. 异面直线与所成角的取值范围是 D. 三棱锥的体积不变
【答案】ABD
三.填空题(本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上.)
13. 若直线与垂直,则实数______.
【答案】
14. 已知圆与圆相交于,两点,则直线的方程为______.
【答案】
15. 己知复数,满足,,若(为虚数单位),则______.
【答案】
16. 已知圆锥的母线长为2,轴截面是过该圆锥顶点的所有截面中面积最大的一个,则该圆锥的表面积的最大值为______.
【答案】
四.解答题(本大题共6小题,共70分.请将正确答案做在答题卷相应位置,要有必要的推理或证明过程.)
17. 设向量,,.
(1)若向量,求.
(2)若向量与向量的夹角为,求.
【答案】(1);(2)或.
18. 的内角,,的对边分别为,,,.
(1)求角的大小;
(2)若,求的面积的最大值.
【答案】(1);(2)
19. 如图,在四棱锥中,底面是正方形,侧棱底面,,、分别是、中点.
(1)求证:平面;
(2)求与面所成角的正弦值.
【答案】(1)见解析;(2)
20. 如图,现有两辆汽车同时从地出发,沿各自路径匀速前往地,汽车甲路线为,汽车乙路线,两车在地汇合后共同前往下一个目的地.已知km,km,km,甲的行驶速度为km/h,乙的行驶速度为km/h.
(1)求乙到达地这一时刻的甲、乙两车之间的距离;
(2)已知两车车上都配有通话器,通话器有效通话距离不超过km,从乙到达地这一时刻算起,甲乙无法通话的时间为多长?
【答案】(1);(2)小时.
21. 如图,已知在三棱柱中,四边形为正方形,,,、分别是、的中点,点是线段上的动点.
(1)证明:;
(2)若,若,求平面与平面所成锐二面角余弦值.
【答案】(1)证明见解析;(2)
22. 已知圆心在第一象限,半径为的圆与轴相切,且与轴正半轴交于,两点(在左侧),(为坐标原点).
(1)求圆的标准方程;
(2)过点任作一条直线与圆相交于,两点.
①证明:为定值;②求的最小值.
【答案】(1);(2)①,证明见解析,②
数学试题
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 直线的倾斜角是( )
A. B. C. D.
2. 复数(为虚数单位)的虚部为( )
A. B. C. D.
3. 在中,内角,,的对边分别为,,,若,,,则角为( )
A. 30° B. 30°或150° C. 60° D. 60°或120°
4. 已知,为两条不同的直线,,为两个不同的平面,则下列说法正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
5. 直线与圆交于、两点,则( )
A. 2 B. C. 6 D.
6. 已知与是直线(为常数)上两个不同的点,则关于和的交点情况是( )
A. 无论,,如何,总有唯一交点 B. 存在,,使之有无穷多个交点
C. 无论,,如何,总是无交点 D. 存在,,使之无交点
7. 如图,在正三棱柱中,,则直线与所成角的余弦值为( )
A. B. C. D.
8. 已知点为直线上的一个动点,过点作圆的两条切线,切点分别为,,则四边形面积的最小值为( )
A. B. C. D.
二.选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分.)
9. 复数的共轭复数记为,则下列运算结果一定是实数的是( )
A. B. C. D.
10. 如果,,那么直线经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
11. 在菱形中,,,,分别为,的中点,则( )
A. B.
C. 在方向上的投影向量的模为2 D.
12. 在正方体中,点在线段上运动,下列说法正确的是( )
A. 平面平面 B. 平面
C. 异面直线与所成角的取值范围是 D. 三棱锥的体积不变
三.填空题(本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上.)
13. 若直线与垂直,则实数______.
14. 已知圆与圆相交于,两点,则直线的方程为______.
15. 己知复数,满足,,若(为虚数单位),则______.
16. 已知圆锥的母线长为2,轴截面是过该圆锥顶点的所有截面中面积最大的一个,则该圆锥的表面积的最大值为______.
四.解答题(本大题共6小题,共70分.请将正确答案做在答题卷相应位置,要有必要的推理或证明过程.)
17. 设向量,,.
(1)若向量,求.
(2)若向量与向量的夹角为,求.
18. 的内角,,的对边分别为,,,.
(1)求角的大小;
(2)若,求的面积的最大值.
19. 如图,在四棱锥中,底面是正方形,侧棱底面,,、分别是、中点.
(1)求证:平面;
(2)求与面所成角的正弦值.
20. 如图,现有两辆汽车同时从地出发,沿各自路径匀速前往地,汽车甲路线为,汽车乙路线,两车在地汇合后共同前往下一个目的地.已知km,km,km,甲的行驶速度为km/h,乙的行驶速度为km/h.
(1)求乙到达地这一时刻的甲、乙两车之间的距离;
(2)已知两车车上都配有通话器,通话器有效通话距离不超过km,从乙到达地这一时刻算起,甲乙无法通话的时间为多长?
21. 如图,已知在三棱柱中,四边形为正方形,,,、分别是、的中点,点是线段上的动点.
(1)证明:;
(2)若,若,求平面与平面所成锐二面角余弦值.
22. 已知圆心在第一象限,半径为的圆与轴相切,且与轴正半轴交于,两点(在左侧),(为坐标原点).
(1)求圆的标准方程;
(2)过点任作一条直线与圆相交于,两点.
①证明:为定值;②求的最小值.
重庆八中2020—2021学年度(下)期末考试高一年级
数学试题 答案版
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 直线的倾斜角是( )
A. B. C. D.
【答案】D
2. 复数(为虚数单位)的虚部为( )
A. B. C. D.
【答案】C
3. 在中,内角,,的对边分别为,,,若,,,则角为( )
A. 30° B. 30°或150° C. 60° D. 60°或120°
【答案】A
4. 已知,为两条不同的直线,,为两个不同的平面,则下列说法正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
【答案】D
5. 直线与圆交于、两点,则( )
A. 2 B. C. 6 D.
【答案】B
6. 已知与是直线(为常数)上两个不同的点,则关于和的交点情况是( )
A. 无论,,如何,总有唯一交点 B. 存在,,使之有无穷多个交点
C. 无论,,如何,总是无交点 D. 存在,,使之无交点
【答案】A
7. 如图,在正三棱柱中,,则直线与所成角的余弦值为( )
A. B. C. D.
【答案】D
8. 已知点为直线上的一个动点,过点作圆的两条切线,切点分别为,,则四边形面积的最小值为( )
A. B. C. D.
【答案】C
二.选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分.)
9. 复数的共轭复数记为,则下列运算结果一定是实数的是( )
A. B. C. D.
【答案】AC
10. 如果,,那么直线经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】ACD
11. 在菱形中,,,,分别为,的中点,则( )
A. B.
C. 在方向上的投影向量的模为2 D.
【答案】ACD
12. 在正方体中,点在线段上运动,下列说法正确的是( )
A. 平面平面 B. 平面
C. 异面直线与所成角的取值范围是 D. 三棱锥的体积不变
【答案】ABD
三.填空题(本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上.)
13. 若直线与垂直,则实数______.
【答案】
14. 已知圆与圆相交于,两点,则直线的方程为______.
【答案】
15. 己知复数,满足,,若(为虚数单位),则______.
【答案】
16. 已知圆锥的母线长为2,轴截面是过该圆锥顶点的所有截面中面积最大的一个,则该圆锥的表面积的最大值为______.
【答案】
四.解答题(本大题共6小题,共70分.请将正确答案做在答题卷相应位置,要有必要的推理或证明过程.)
17. 设向量,,.
(1)若向量,求.
(2)若向量与向量的夹角为,求.
【答案】(1);(2)或.
18. 的内角,,的对边分别为,,,.
(1)求角的大小;
(2)若,求的面积的最大值.
【答案】(1);(2)
19. 如图,在四棱锥中,底面是正方形,侧棱底面,,、分别是、中点.
(1)求证:平面;
(2)求与面所成角的正弦值.
【答案】(1)见解析;(2)
20. 如图,现有两辆汽车同时从地出发,沿各自路径匀速前往地,汽车甲路线为,汽车乙路线,两车在地汇合后共同前往下一个目的地.已知km,km,km,甲的行驶速度为km/h,乙的行驶速度为km/h.
(1)求乙到达地这一时刻的甲、乙两车之间的距离;
(2)已知两车车上都配有通话器,通话器有效通话距离不超过km,从乙到达地这一时刻算起,甲乙无法通话的时间为多长?
【答案】(1);(2)小时.
21. 如图,已知在三棱柱中,四边形为正方形,,,、分别是、的中点,点是线段上的动点.
(1)证明:;
(2)若,若,求平面与平面所成锐二面角余弦值.
【答案】(1)证明见解析;(2)
22. 已知圆心在第一象限,半径为的圆与轴相切,且与轴正半轴交于,两点(在左侧),(为坐标原点).
(1)求圆的标准方程;
(2)过点任作一条直线与圆相交于,两点.
①证明:为定值;②求的最小值.
【答案】(1);(2)①,证明见解析,②
同课章节目录
