4.1 生活中的立体图形 同步课时作业2021-2022学年华东师大版数学七年级上册(Word版含答案)
文档属性
| 名称 | 4.1 生活中的立体图形 同步课时作业2021-2022学年华东师大版数学七年级上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 307.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:00:00 | ||
图片预览


文档简介
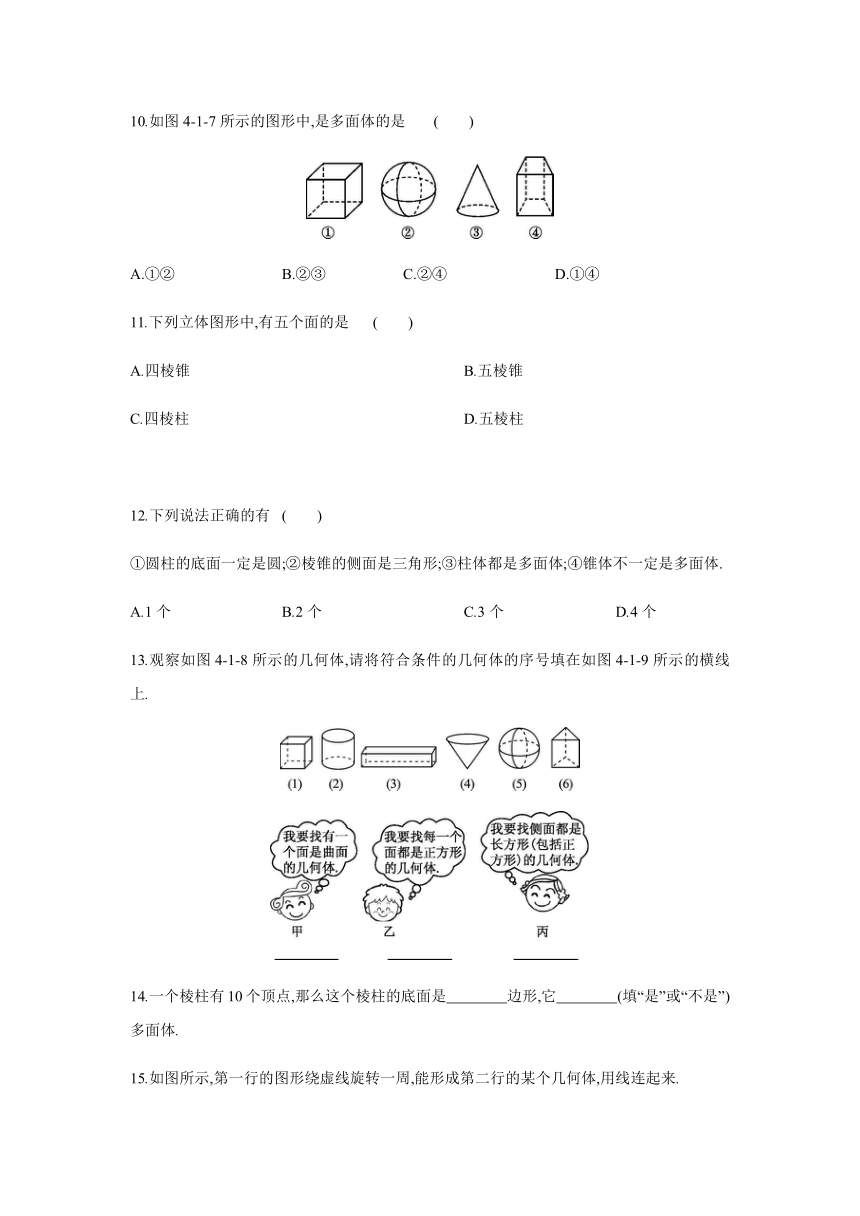
4.1 生活中的立体图形
知识点
1 立体图形
1.下列物体的形状类似于球的是
( )
A.茶叶筒
B.羽毛球
C.乒乓球
D.日光灯管
2.[2019·白银]
下列四个几何体中,是三棱柱的为
( )
3.下列几何体中,是圆锥的为
( )
4.如图4-1-3,含有曲面的几何体编号是
( )
A.①②
B.①③
C.②③
D.②④
5.填空:(1)三棱柱有 个面, 个顶点, 条棱;?
(2)四棱柱有 个面, 个顶点, 条棱;?
(3)五棱柱有 个面, 个顶点, 条棱;?
(4)十棱柱有 个面, 个顶点, 条棱;?
(5)n棱柱有 个面, 个顶点, 条棱.?
知识点
2 立体图形的分类
6.四棱柱、长方体和正方体之间的包含关系是图4-1-4中的
( )
7.如图4-1-5,不是锥体的是 .(填序号)?
8.将图4-1-6中的几何体进行分类,并说明理由.
知识点
3 多面体
9.下列几何体都是由平面围成的是
( )
A.圆柱
B.圆锥
C.四棱柱
D.球
10.如图4-1-7所示的图形中,是多面体的是
( )
A.①②
B.②③
C.②④
D.①④
11.下列立体图形中,有五个面的是
( )
A.四棱锥
B.五棱锥
C.四棱柱
D.五棱柱
12.下列说法正确的有
( )
①圆柱的底面一定是圆;②棱锥的侧面是三角形;③柱体都是多面体;④锥体不一定是多面体.
A.1个
B.2个
C.3个
D.4个
13.观察如图4-1-8所示的几何体,请将符合条件的几何体的序号填在如图4-1-9所示的横线上.
14.一个棱柱有10个顶点,那么这个棱柱的底面是 边形,它 (填“是”或“不是”)多面体.?
15.如图所示,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
16.根据下列描述,分别判断该立体图形的名称:
(1)一个立体图形是锥体,它的底面是六边形;
(2)一个立体图形,无论怎样截,得到的截面都是圆.
17.观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20
cm,侧棱长为8
cm,则它的侧面积为多少?
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察如图所示的几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
?
正方体
8
6
12
正八面体
?
8
12
正十二面体
20
12
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .?
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .?
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x个,八边形的个数为y个,则x+y= .?
答案
1.C 2.C 3.D 4.C
5.(1)5 6 9 (2)6 8 12
(3)7 10 15 (4)12 20 30
(5)(n+2) 2n 3n
6.A 7.(3)
8.解:答案不唯一,如若按组成几何体的面的平或曲来划分:①②⑥⑦是一类,组成它的各面全是平面;③④⑤是一类,组成它的面至少有一个是曲面.
若按柱体、锥体、球体来划分:①②④⑦是一类,即柱体;⑤⑥是一类,即锥体;③是一类,即球体.
9.C 10.D
11.A [解析]
四棱锥由一个底面、四个侧面组成,共五个面.故选A.
12.C [解析]
①②④正确.
13.甲:(2)(4)(5) 乙:(1) 丙:(1)(3)(6)
14.五 是 [解析]
一个棱柱有10个顶点,根据特点可知它是五棱柱,则底面是五边形,它是多面体.
15.解:如图所示.
16.解:(1)六棱锥.(2)球.
17.解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形.
(2)侧面的个数与底面多边形的边数相等,都为4.
(3)它的侧面积为20×8=160(cm2).
18.(1)第一行:6 第二行:6 V+F-E=2
(2)20 (3)14
[解析]
(1)四面体的棱数为6;正八面体的顶点数为6;关系式为V+F-E=2.
(2)由题意得F-8+F-30=2,解得F=20.
故答案为20.
(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,
所以共有24×3÷2=36(条)棱,
那么24+F-36=2,解得F=14,
所以x+y=14.
知识点
1 立体图形
1.下列物体的形状类似于球的是
( )
A.茶叶筒
B.羽毛球
C.乒乓球
D.日光灯管
2.[2019·白银]
下列四个几何体中,是三棱柱的为
( )
3.下列几何体中,是圆锥的为
( )
4.如图4-1-3,含有曲面的几何体编号是
( )
A.①②
B.①③
C.②③
D.②④
5.填空:(1)三棱柱有 个面, 个顶点, 条棱;?
(2)四棱柱有 个面, 个顶点, 条棱;?
(3)五棱柱有 个面, 个顶点, 条棱;?
(4)十棱柱有 个面, 个顶点, 条棱;?
(5)n棱柱有 个面, 个顶点, 条棱.?
知识点
2 立体图形的分类
6.四棱柱、长方体和正方体之间的包含关系是图4-1-4中的
( )
7.如图4-1-5,不是锥体的是 .(填序号)?
8.将图4-1-6中的几何体进行分类,并说明理由.
知识点
3 多面体
9.下列几何体都是由平面围成的是
( )
A.圆柱
B.圆锥
C.四棱柱
D.球
10.如图4-1-7所示的图形中,是多面体的是
( )
A.①②
B.②③
C.②④
D.①④
11.下列立体图形中,有五个面的是
( )
A.四棱锥
B.五棱锥
C.四棱柱
D.五棱柱
12.下列说法正确的有
( )
①圆柱的底面一定是圆;②棱锥的侧面是三角形;③柱体都是多面体;④锥体不一定是多面体.
A.1个
B.2个
C.3个
D.4个
13.观察如图4-1-8所示的几何体,请将符合条件的几何体的序号填在如图4-1-9所示的横线上.
14.一个棱柱有10个顶点,那么这个棱柱的底面是 边形,它 (填“是”或“不是”)多面体.?
15.如图所示,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
16.根据下列描述,分别判断该立体图形的名称:
(1)一个立体图形是锥体,它的底面是六边形;
(2)一个立体图形,无论怎样截,得到的截面都是圆.
17.观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20
cm,侧棱长为8
cm,则它的侧面积为多少?
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察如图所示的几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
?
正方体
8
6
12
正八面体
?
8
12
正十二面体
20
12
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .?
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .?
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x个,八边形的个数为y个,则x+y= .?
答案
1.C 2.C 3.D 4.C
5.(1)5 6 9 (2)6 8 12
(3)7 10 15 (4)12 20 30
(5)(n+2) 2n 3n
6.A 7.(3)
8.解:答案不唯一,如若按组成几何体的面的平或曲来划分:①②⑥⑦是一类,组成它的各面全是平面;③④⑤是一类,组成它的面至少有一个是曲面.
若按柱体、锥体、球体来划分:①②④⑦是一类,即柱体;⑤⑥是一类,即锥体;③是一类,即球体.
9.C 10.D
11.A [解析]
四棱锥由一个底面、四个侧面组成,共五个面.故选A.
12.C [解析]
①②④正确.
13.甲:(2)(4)(5) 乙:(1) 丙:(1)(3)(6)
14.五 是 [解析]
一个棱柱有10个顶点,根据特点可知它是五棱柱,则底面是五边形,它是多面体.
15.解:如图所示.
16.解:(1)六棱锥.(2)球.
17.解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形.
(2)侧面的个数与底面多边形的边数相等,都为4.
(3)它的侧面积为20×8=160(cm2).
18.(1)第一行:6 第二行:6 V+F-E=2
(2)20 (3)14
[解析]
(1)四面体的棱数为6;正八面体的顶点数为6;关系式为V+F-E=2.
(2)由题意得F-8+F-30=2,解得F=20.
故答案为20.
(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,
所以共有24×3÷2=36(条)棱,
那么24+F-36=2,解得F=14,
所以x+y=14.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
