5.1.3 同位角、内错角、同旁内角 同步课时作业 2021-2022学年华东师大版数学七年级上册(Word版含答案)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角 同步课时作业 2021-2022学年华东师大版数学七年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 17:27:33 | ||
图片预览


文档简介
5.1.3 同位角、内错角、同旁内角
知识点
1 同位角
1.[2020·河池]
如图,直线a,b被直线c所截,则∠1与∠2的位置关系是
( )
A.同位角
B.内错角
C.同旁内角
D.邻补角
图
2.如图,∠1和∠2是直线 和直线 被直线 所截得到的 .?
知识点
2 内错角
3.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是 .?
图
4.如图,∠B的内错角是
( )
A.∠1
B.∠2
C.∠3
D.∠4
知识点
3 同旁内角
5.如图,∠DCB和∠ABC是直线 和 被直线 所截而成的 角.?
图
6.如图,与∠1是同旁内角的是
( )
A.∠2
B.∠3
C.∠4
D.∠5
知识点
4 三类角的综合
7.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是
( )
A.∠4,∠2
B.∠2,∠6
C.∠5,∠4
D.∠2,∠4
图
8.如图,下列说法错误的是
( )
A.∠C与∠1是内错角
B.∠A与∠B是同旁内角
C.∠2与∠3是内错角
D.∠A与∠3是同位角
9.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .?
10.如图,∠B和∠CAB是直线 , 被直线 所截而成的 角;∠C和∠DAC是直线 , 被直线 所截而成的 角.?
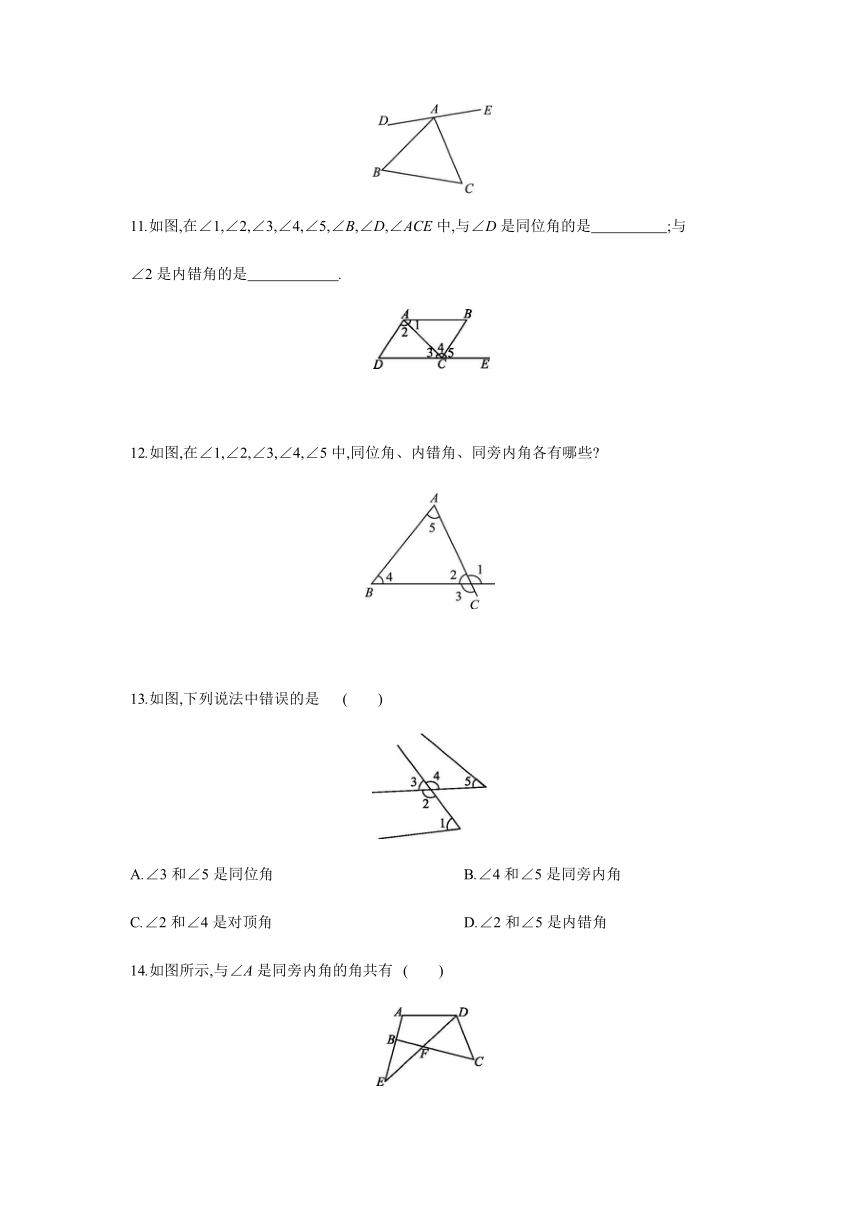
11.如图,在∠1,∠2,∠3,∠4,∠5,∠B,∠D,∠ACE中,与∠D是同位角的是
;与
∠2是内错角的是 .?
12.如图,在∠1,∠2,∠3,∠4,∠5中,同位角、内错角、同旁内角各有哪些?
13.如图,下列说法中错误的是
( )
A.∠3和∠5是同位角
B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角
D.∠2和∠5是内错角
14.如图所示,与∠A是同旁内角的角共有
( )
A.2个
B.3个
C.4个
D.5个
15.如图所示,能与∠1构成同位角的角有
个.?
16.如图所示,BF,DE相交于点A,BG与BF交于点B,与AC交于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角、同旁内角;
(3)指出FB,BC被AC所截形成的内错角、同旁内角.
17.读图①~④,回答下列问题.
(1)请你写出图①、图②、图③和图④中分别有几对同旁内角;
(2)观察图形,请写出图(n是正整数)中有几对同旁内角.
18.如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1∠9
∠3.
路径2:∠1∠12∠6∠10∠3.
试一试:(1)从起始角∠1跳到终点角∠8,试写出一种路径;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8?若能,写出路径.
答案
1.A 2.c b a 同位角
3.内错角 4.D
5.DE AB BC 同旁内
6.D [解析]
A项,∠1和∠2是对顶角,不是同旁内角,故A不符合题意;
B项,∠1和∠3是同位角,不是同旁内角,故B不符合题意;
C项,∠1和∠4是内错角,不是同旁内角,故C不符合题意;
D项,∠1和∠5是同旁内角,故D符合题意.故选D.
7.B 8.C
9.80° 80° 100°
10.AC BC AB 同旁内 DE BC AC
同旁内
11.∠5,∠ACE ∠4,∠ACE
12.解:同位角:∠1与∠4,∠5与∠3;内错角:∠1与∠5,∠3与∠4;同旁内角:∠2与∠4,∠4与∠5,∠2与∠5.
13.D
14.C [解析]
与∠A是同旁内角的角有∠ABC,∠ADC,∠ADE,∠AED,共有4个.故选C.
15.3
16.解:(1)同位角:∠FAE和∠B;
内错角:∠B和∠DAB;
同旁内角:∠EAB和∠B.
(2)内错角:∠EAC和∠BCA,∠DAC和∠ACG;
同旁内角:∠EAC和∠ACG,∠DAC和∠BCA.
(3)内错角:∠BAC和∠ACG,∠FAC和∠BCA;
同旁内角:∠BAC和∠BCA,∠FAC和∠ACG.
17.解:(1)图①中有2对同旁内角;图②中有8对同旁内角;图③中有18对同旁内角;图④中有32对同旁内角.
(2)图(n是正整数)中有2n2对同旁内角.
18.解:(1)答案不唯一,如∠1∠12∠8.
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8,其路径为∠1∠10∠5∠8.
知识点
1 同位角
1.[2020·河池]
如图,直线a,b被直线c所截,则∠1与∠2的位置关系是
( )
A.同位角
B.内错角
C.同旁内角
D.邻补角
图
2.如图,∠1和∠2是直线 和直线 被直线 所截得到的 .?
知识点
2 内错角
3.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是 .?
图
4.如图,∠B的内错角是
( )
A.∠1
B.∠2
C.∠3
D.∠4
知识点
3 同旁内角
5.如图,∠DCB和∠ABC是直线 和 被直线 所截而成的 角.?
图
6.如图,与∠1是同旁内角的是
( )
A.∠2
B.∠3
C.∠4
D.∠5
知识点
4 三类角的综合
7.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是
( )
A.∠4,∠2
B.∠2,∠6
C.∠5,∠4
D.∠2,∠4
图
8.如图,下列说法错误的是
( )
A.∠C与∠1是内错角
B.∠A与∠B是同旁内角
C.∠2与∠3是内错角
D.∠A与∠3是同位角
9.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .?
10.如图,∠B和∠CAB是直线 , 被直线 所截而成的 角;∠C和∠DAC是直线 , 被直线 所截而成的 角.?
11.如图,在∠1,∠2,∠3,∠4,∠5,∠B,∠D,∠ACE中,与∠D是同位角的是
;与
∠2是内错角的是 .?
12.如图,在∠1,∠2,∠3,∠4,∠5中,同位角、内错角、同旁内角各有哪些?
13.如图,下列说法中错误的是
( )
A.∠3和∠5是同位角
B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角
D.∠2和∠5是内错角
14.如图所示,与∠A是同旁内角的角共有
( )
A.2个
B.3个
C.4个
D.5个
15.如图所示,能与∠1构成同位角的角有
个.?
16.如图所示,BF,DE相交于点A,BG与BF交于点B,与AC交于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角、同旁内角;
(3)指出FB,BC被AC所截形成的内错角、同旁内角.
17.读图①~④,回答下列问题.
(1)请你写出图①、图②、图③和图④中分别有几对同旁内角;
(2)观察图形,请写出图(n是正整数)中有几对同旁内角.
18.如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1∠9
∠3.
路径2:∠1∠12∠6∠10∠3.
试一试:(1)从起始角∠1跳到终点角∠8,试写出一种路径;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8?若能,写出路径.
答案
1.A 2.c b a 同位角
3.内错角 4.D
5.DE AB BC 同旁内
6.D [解析]
A项,∠1和∠2是对顶角,不是同旁内角,故A不符合题意;
B项,∠1和∠3是同位角,不是同旁内角,故B不符合题意;
C项,∠1和∠4是内错角,不是同旁内角,故C不符合题意;
D项,∠1和∠5是同旁内角,故D符合题意.故选D.
7.B 8.C
9.80° 80° 100°
10.AC BC AB 同旁内 DE BC AC
同旁内
11.∠5,∠ACE ∠4,∠ACE
12.解:同位角:∠1与∠4,∠5与∠3;内错角:∠1与∠5,∠3与∠4;同旁内角:∠2与∠4,∠4与∠5,∠2与∠5.
13.D
14.C [解析]
与∠A是同旁内角的角有∠ABC,∠ADC,∠ADE,∠AED,共有4个.故选C.
15.3
16.解:(1)同位角:∠FAE和∠B;
内错角:∠B和∠DAB;
同旁内角:∠EAB和∠B.
(2)内错角:∠EAC和∠BCA,∠DAC和∠ACG;
同旁内角:∠EAC和∠ACG,∠DAC和∠BCA.
(3)内错角:∠BAC和∠ACG,∠FAC和∠BCA;
同旁内角:∠BAC和∠BCA,∠FAC和∠ACG.
17.解:(1)图①中有2对同旁内角;图②中有8对同旁内角;图③中有18对同旁内角;图④中有32对同旁内角.
(2)图(n是正整数)中有2n2对同旁内角.
18.解:(1)答案不唯一,如∠1∠12∠8.
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8,其路径为∠1∠10∠5∠8.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
