5.2.3平行线的性质 同步课时作业 2021-2022学年华东师大版数学七年级上册(Word版含答案)
文档属性
| 名称 | 5.2.3平行线的性质 同步课时作业 2021-2022学年华东师大版数学七年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 17:27:43 | ||
图片预览




文档简介
5.2.3 平行线的性质
知识点
1 两直线平行,同位角相等
1.[2020·宿迁]
如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数为
( )
A.40°
B.50°
C.130°
D.150°
图
2.[2020·兰州]
如图,AB∥CD,AE∥CF,∠A=50°,则∠C等于
( )
A.40°
B.50°
C.60°
D.70°
3.[2019·娄底改编]
如图,AB∥CD,AC∥BD,∠1=28°,求∠2的度数.
知识点
2 两直线平行,内错角相等
4.[2020·柳州]
如图,直线l1,l2被直线l3所截,l1∥l2,已知∠1=80°,则∠2= °.?
图
5.如图,已知AB∥CD,EB∥CF,说明∠1=∠2的推理过程如下,请完成填空.
解:因为AB∥CD(已知),
所以∠ABC=∠BCD( ).?
因为EB∥CF(已知),
所以 = ( ),?
所以∠ABC-∠EBC= ,?
即∠1=∠2.
知识点
3 两直线平行,同旁内角互补
6.[2020·济南]
如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD的度数为
( )
A.35°
B.45°
C.55°
D.70°
图
7.如图,直线AB∥CD,直线EF与AB,CD分别相交于点E,F,∠BEF的平分线EN与CD相交于点N.若∠1=65°,则∠2= °.?
8.如图所示,已知∠1=∠2,∠D=70°,求∠B的度数.
知识点
4 图形的平行移动
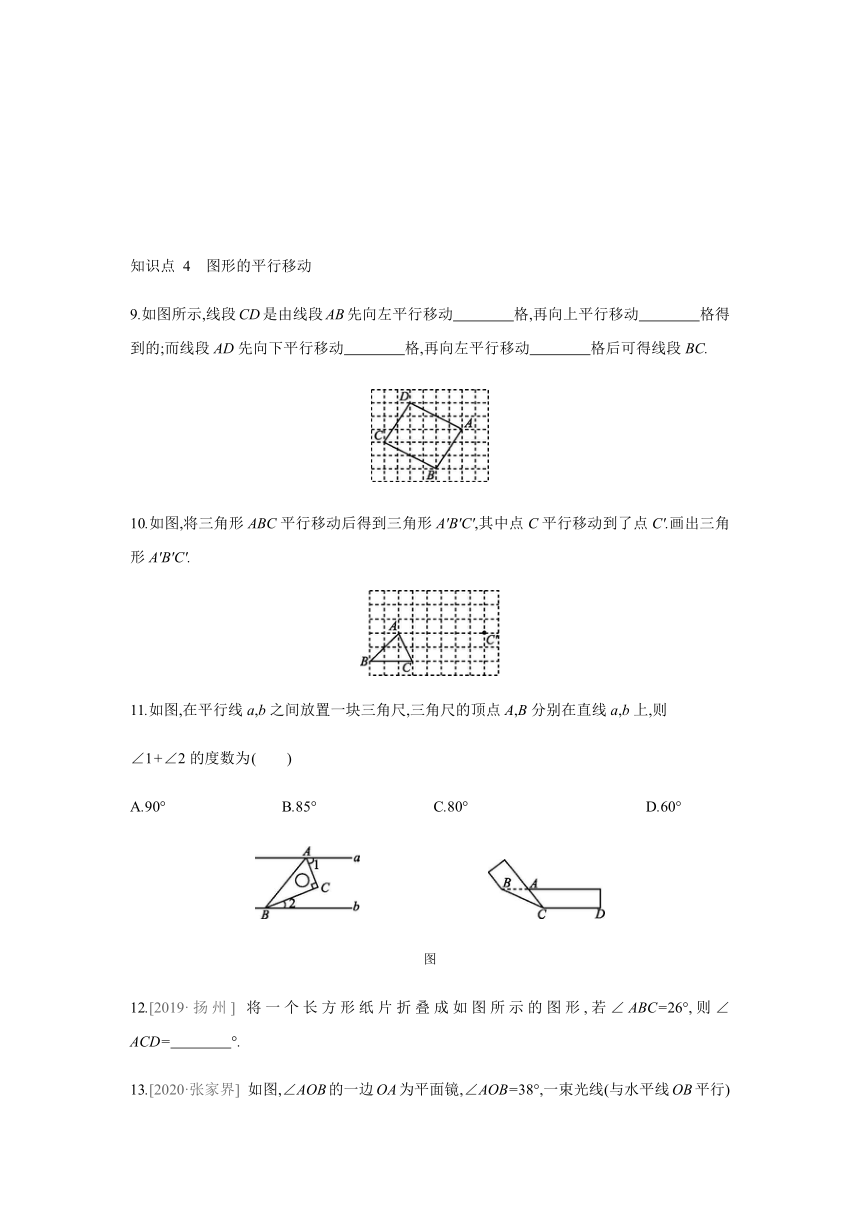
9.如图所示,线段CD是由线段AB先向左平行移动 格,再向上平行移动 格得到的;而线段AD先向下平行移动 格,再向左平行移动 格后可得线段BC.?
10.如图,将三角形ABC平行移动后得到三角形A'B'C',其中点C平行移动到了点C'.画出三角形A'B'C'.
11.如图,在平行线a,b之间放置一块三角尺,三角尺的顶点A,B分别在直线a,b上,则
∠1+∠2的度数为
( )
A.90°
B.85°
C.80°
D.60°
图
12.[2019·扬州]
将一个长方形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD= °.?
13.[2020·张家界]
如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是
度.?
图
14.一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE.若∠BCD=150°,则∠ABC= °.?
15.如图,AB∥CD,点E在AC上,∠1=∠B,BE⊥DE,试说明:∠2=∠D.
16.已知:如图,在三角形ABC中,作AD⊥BC于点D,作DE∥AB交AC于点E,再在AB上取一点F,作∠BFG=∠ADE交BC于点G.
试说明:FG⊥BC.
17.如图,直线AB∥CD,E为直线AB,CD之间的一点,完成以下问题:
(1)如图①,若∠B=15°,∠BED=90°,则∠D= °;?
(2)如图②,若∠B=α,∠D=β,求出∠BED的度数(用α,β表示);
(3)如图③,若∠B=α,∠C=β,则α,β与∠BEC之间有什么等量关系?并说明理由.
答案
1.B
2.B [解析]
如图,
∵AE∥CF,∠A=50°,
∴∠1=∠A=50°.
∵AB∥CD,
∴∠C=∠1=50°.
故选B.
3.解:因为AC∥BD,所以∠1=∠A.
因为AB∥CD,所以∠2=∠A,
所以∠2=∠1=28°.
4.80
5.两直线平行,内错角相等 ∠EBC ∠BCF 两直线平行,内错角相等 ∠BCD-∠BCF
6.C
7.50
8.[解析]
易得AB∥CD,所以∠B+∠D=180°,进而可求得∠B=110°.
解:因为∠2=∠DFE,且∠1=∠2,
所以∠1=∠DFE,
所以AB∥CD,
所以∠B+∠D=180°.
因为∠D=70°,
所以∠B=180°-∠D=110°.
9.4 2 3 2 [解析]
看清上、下、左、右,数对方格即可.
10.解:图中的三角形A'B'C'即为所求.
11.A
12.128 [解析]
如图,延长DC.
由题意可得∠ABC=∠BCE=∠BCA=26°,
则∠ACD=180°-26°-26°=128°.
故答案为128.
13.76 [解析]
∵DC∥OB,
∴∠ADC=∠AOB=38°.
由光线的反射定理易得
∠ODE=∠ADC=38°,
∴∠CDE=180°-38°-38°=104°.
∵DC∥OB,
∴∠CDE+∠DEB=180°,
∴∠DEB=180°-104°=76°.
故答案为:76.
14.120
15.解:如图,过点E作EF∥AB,
则∠B=∠3.
∵∠1=∠B,
∴∠1=∠3.
∵BE⊥DE,
∴∠3+∠4=90°,
∴∠1+∠2=180°-(∠3+∠4)=90°,
∴∠2=∠4.
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠4=∠D.
∴∠2=∠D.
16.解:∵AD⊥BC,
∴∠ADB=90°.
∵DE∥AB,
∴∠BAD=∠ADE.
∵∠BFG=∠ADE,
∴∠BAD=∠BFG,
∴AD∥FG,
∴∠FGB=∠ADB=90°,∴FG⊥BC.
17.解:(1)75 [解析]
如图①,过点E作EF∥AB.又∵AB∥CD,∴EF∥CD.∵∠B=15°,∴∠BEF=15°.∵∠BED=90°,∴∠DEF=75°.∵EF∥CD,∴∠D=75°.故答案为:75.
(2)如图②,过点E作EF∥AB.
∵AB∥CD,∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°.
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β.
(3)猜想:∠BEC=180°-α+β.理由:如图③,过点E作EF∥AB,则∠BEF=180°-∠B=180°-α.
∵AB∥EF,AB∥CD,
∴EF∥CD,∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.
知识点
1 两直线平行,同位角相等
1.[2020·宿迁]
如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数为
( )
A.40°
B.50°
C.130°
D.150°
图
2.[2020·兰州]
如图,AB∥CD,AE∥CF,∠A=50°,则∠C等于
( )
A.40°
B.50°
C.60°
D.70°
3.[2019·娄底改编]
如图,AB∥CD,AC∥BD,∠1=28°,求∠2的度数.
知识点
2 两直线平行,内错角相等
4.[2020·柳州]
如图,直线l1,l2被直线l3所截,l1∥l2,已知∠1=80°,则∠2= °.?
图
5.如图,已知AB∥CD,EB∥CF,说明∠1=∠2的推理过程如下,请完成填空.
解:因为AB∥CD(已知),
所以∠ABC=∠BCD( ).?
因为EB∥CF(已知),
所以 = ( ),?
所以∠ABC-∠EBC= ,?
即∠1=∠2.
知识点
3 两直线平行,同旁内角互补
6.[2020·济南]
如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD的度数为
( )
A.35°
B.45°
C.55°
D.70°
图
7.如图,直线AB∥CD,直线EF与AB,CD分别相交于点E,F,∠BEF的平分线EN与CD相交于点N.若∠1=65°,则∠2= °.?
8.如图所示,已知∠1=∠2,∠D=70°,求∠B的度数.
知识点
4 图形的平行移动
9.如图所示,线段CD是由线段AB先向左平行移动 格,再向上平行移动 格得到的;而线段AD先向下平行移动 格,再向左平行移动 格后可得线段BC.?
10.如图,将三角形ABC平行移动后得到三角形A'B'C',其中点C平行移动到了点C'.画出三角形A'B'C'.
11.如图,在平行线a,b之间放置一块三角尺,三角尺的顶点A,B分别在直线a,b上,则
∠1+∠2的度数为
( )
A.90°
B.85°
C.80°
D.60°
图
12.[2019·扬州]
将一个长方形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD= °.?
13.[2020·张家界]
如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是
度.?
图
14.一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE.若∠BCD=150°,则∠ABC= °.?
15.如图,AB∥CD,点E在AC上,∠1=∠B,BE⊥DE,试说明:∠2=∠D.
16.已知:如图,在三角形ABC中,作AD⊥BC于点D,作DE∥AB交AC于点E,再在AB上取一点F,作∠BFG=∠ADE交BC于点G.
试说明:FG⊥BC.
17.如图,直线AB∥CD,E为直线AB,CD之间的一点,完成以下问题:
(1)如图①,若∠B=15°,∠BED=90°,则∠D= °;?
(2)如图②,若∠B=α,∠D=β,求出∠BED的度数(用α,β表示);
(3)如图③,若∠B=α,∠C=β,则α,β与∠BEC之间有什么等量关系?并说明理由.
答案
1.B
2.B [解析]
如图,
∵AE∥CF,∠A=50°,
∴∠1=∠A=50°.
∵AB∥CD,
∴∠C=∠1=50°.
故选B.
3.解:因为AC∥BD,所以∠1=∠A.
因为AB∥CD,所以∠2=∠A,
所以∠2=∠1=28°.
4.80
5.两直线平行,内错角相等 ∠EBC ∠BCF 两直线平行,内错角相等 ∠BCD-∠BCF
6.C
7.50
8.[解析]
易得AB∥CD,所以∠B+∠D=180°,进而可求得∠B=110°.
解:因为∠2=∠DFE,且∠1=∠2,
所以∠1=∠DFE,
所以AB∥CD,
所以∠B+∠D=180°.
因为∠D=70°,
所以∠B=180°-∠D=110°.
9.4 2 3 2 [解析]
看清上、下、左、右,数对方格即可.
10.解:图中的三角形A'B'C'即为所求.
11.A
12.128 [解析]
如图,延长DC.
由题意可得∠ABC=∠BCE=∠BCA=26°,
则∠ACD=180°-26°-26°=128°.
故答案为128.
13.76 [解析]
∵DC∥OB,
∴∠ADC=∠AOB=38°.
由光线的反射定理易得
∠ODE=∠ADC=38°,
∴∠CDE=180°-38°-38°=104°.
∵DC∥OB,
∴∠CDE+∠DEB=180°,
∴∠DEB=180°-104°=76°.
故答案为:76.
14.120
15.解:如图,过点E作EF∥AB,
则∠B=∠3.
∵∠1=∠B,
∴∠1=∠3.
∵BE⊥DE,
∴∠3+∠4=90°,
∴∠1+∠2=180°-(∠3+∠4)=90°,
∴∠2=∠4.
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠4=∠D.
∴∠2=∠D.
16.解:∵AD⊥BC,
∴∠ADB=90°.
∵DE∥AB,
∴∠BAD=∠ADE.
∵∠BFG=∠ADE,
∴∠BAD=∠BFG,
∴AD∥FG,
∴∠FGB=∠ADB=90°,∴FG⊥BC.
17.解:(1)75 [解析]
如图①,过点E作EF∥AB.又∵AB∥CD,∴EF∥CD.∵∠B=15°,∴∠BEF=15°.∵∠BED=90°,∴∠DEF=75°.∵EF∥CD,∴∠D=75°.故答案为:75.
(2)如图②,过点E作EF∥AB.
∵AB∥CD,∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°.
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β.
(3)猜想:∠BEC=180°-α+β.理由:如图③,过点E作EF∥AB,则∠BEF=180°-∠B=180°-α.
∵AB∥EF,AB∥CD,
∴EF∥CD,∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
