重庆市杨家坪中学2011-2012学年高二下学期期中考试数学(理)试题
文档属性
| 名称 | 重庆市杨家坪中学2011-2012学年高二下学期期中考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 648.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-16 00:00:00 | ||
图片预览



文档简介
(完卷时间:120分钟 满分:150分)
一.选择题(每小题5分, 共50分)
1.用三段论推理命题:“任何实数的平方大于0,因为a是实数,所以>0”,你认
为这个推理( )
A.大前题错误 B.小前题错误
C.推理形式错误 D.是正确的
2.锐角三角形的面积等于底乘高的一半;直角三角形的面积等于底乘高的一半;钝角三角形的面积等于底乘高的一半。所以,凡是三角形的面积都等于底乘高的一半。以上推理运用的是( )
A、不完全归纳推理 B、 类比推理
C、演绎推理 D、完全归纳推理
3.今天是星期一,再过天,应是星期( ) A.二 B.三 C.四 D.五
4.函数y=f (x)定义域为(a,b),y=f ' (x)在(a,b)上的图象如图,则y=f (x)在区间(a,b)上极大值点的个数为 ( )
A.1 B.2 C.3 D.4
5.. .已知函数 则= ( )
A.1 B. 0 C. D.
6.用反证法证明某命题时,对结论:“自然数,,中恰有一个偶数”正确的反设为( )
A.,,都是奇数 B. ,,都是偶数
C.,,中至少有两个偶数或都是奇数 D. ,,中至少有两个偶数
7. 设复数(为虚数单位),则
( )
A. B. C. D.
8.已知复数 都是实数,且),在复平面内,
Z1、Z2所对应的点与原点组成的三角形是 ( )
A.锐角三角形 B.直角三角形
C.等腰直角三角形 D.等边三角形
9.给出以下命题:
(1)若,则f(x)>0;
(2);
(3)应用微积分基本定理,有, 则F(x)=lnx;
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则;
其中正确命题的个数为 ( )
A.1 B.2 C.3 D.4
10. 由等式
定义映射( )
A、(1,2,3,4) B、(0,3,4,0)
C、 D、
二.填空题(每小题5分,共5小题,共25分)
11. 一个物体的运动方程为,其中的单位是米,的单位是秒,那么物体在2秒末的瞬时速度是___________________ 米/秒
12.化简成形式: 等于_____________
13.设,则_______________
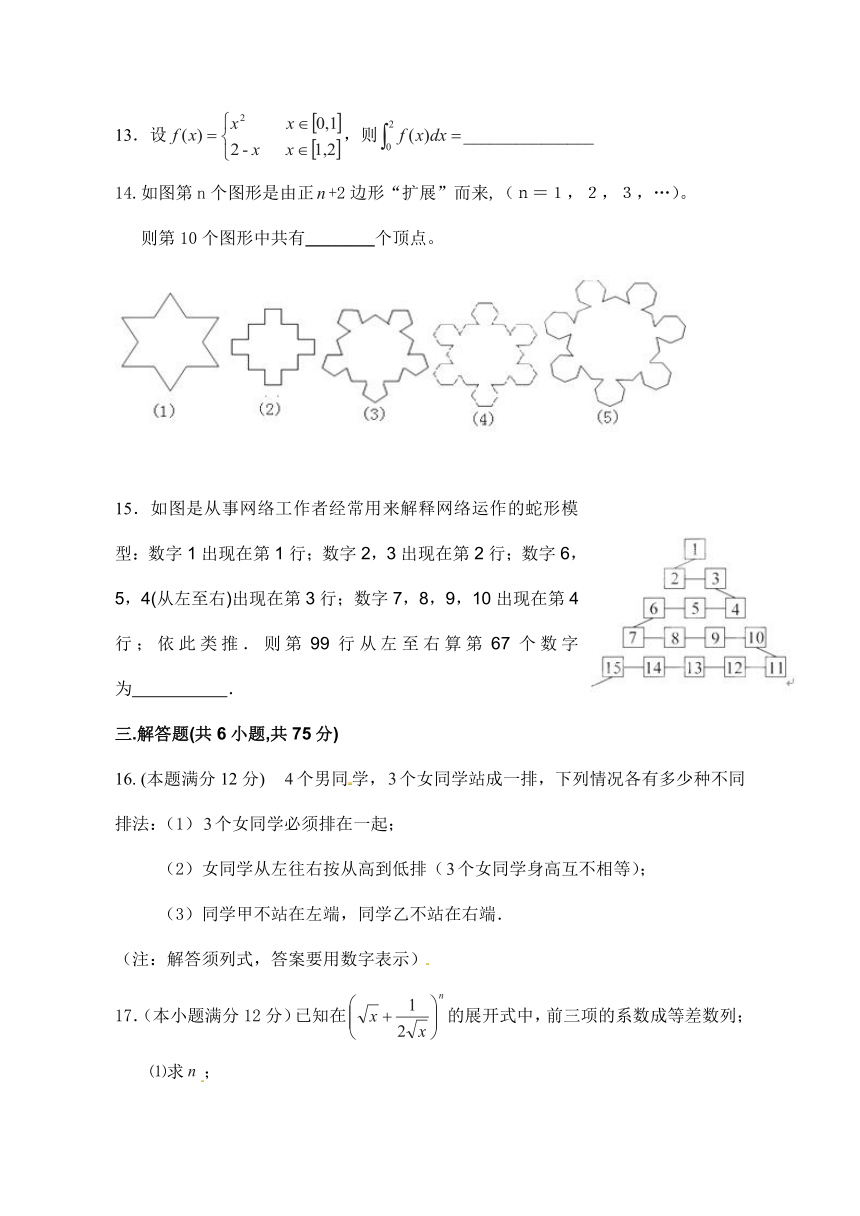
14.如图第n个图形是由正+2边形“扩展”而来,(n=1,2,3,…)。
则第10个图形中共有________个顶点。
15.如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第99行从左至右算第67个数字为 .
三.解答题(共6小题,共75分)
16. (本题满分12分) 个男同学,个女同学站成一排,下列情况各有多少种不同排法:(1)个女同学必须排在一起;
(2)女同学从左往右按从高到低排(个女同学身高互不相等);
(3)同学甲不站在左端,同学乙不站在右端.
(注:解答须列式,答案要用数字表示)
17.(本小题满分12分)已知在的展开式中,前三项的系数成等差数列;
⑴求;
⑵求展开式中的常数项;
⑶求展开式中系数最大的项.
18..(本题满分12分) 已知曲线,
(1) 求曲线在处的切线方程;
(2) 求曲线过点(2,4)的切线方程.
19.(本小题满分12分)
已知函数在处取得极值,
(1)试求实数的值;
(2)试求函数的单调区间;
(3)若对任意,不等式恒成立,求实数的取值范围.
20. (本小题满分13分)设数列的前项和为,且对任意的都有
,
(1)求数列的前三项;
(2)猜想数列的通项公式,并用数学归纳法证明;
(3)求证:对任意都有.
21.(本小题满分14分)
如图所示,已知曲线与曲线交于点、,
直线与曲线、分别相交于点、,连结.
(Ⅰ)写出曲边四边形 (阴影部分)的面积与的函数关系式;
(Ⅱ)求函数在区间上的最大值.
杨家坪中学高2013级高二下期中考试 (理)答案
由题意,得:,∵r∈N,∴r=2或3
∴展开式中系数最大的项为.……………………………13分
19.解:(1)由题意知,∴;对求导可得:.由题意,得,即, ∴;即实数,.…………4分
20.解: (1)令得,,故; 令得,,故; 令得,,故;…………3分
(3)∵,∴,
∴
∴对任意都有.…………13分
(Ⅱ),令,即,
解得或. ……8分
,应舍去.若即时,
,.
在区间上单调递增,的最大值是. ……10分
若 即时,当时,,
当时,.在区间上单调递增,在区间上单调递减.的最大值是
. ……13分
综上所述, ……14分
17.
18.
一.选择题(每小题5分, 共50分)
1.用三段论推理命题:“任何实数的平方大于0,因为a是实数,所以>0”,你认
为这个推理( )
A.大前题错误 B.小前题错误
C.推理形式错误 D.是正确的
2.锐角三角形的面积等于底乘高的一半;直角三角形的面积等于底乘高的一半;钝角三角形的面积等于底乘高的一半。所以,凡是三角形的面积都等于底乘高的一半。以上推理运用的是( )
A、不完全归纳推理 B、 类比推理
C、演绎推理 D、完全归纳推理
3.今天是星期一,再过天,应是星期( ) A.二 B.三 C.四 D.五
4.函数y=f (x)定义域为(a,b),y=f ' (x)在(a,b)上的图象如图,则y=f (x)在区间(a,b)上极大值点的个数为 ( )
A.1 B.2 C.3 D.4
5.. .已知函数 则= ( )
A.1 B. 0 C. D.
6.用反证法证明某命题时,对结论:“自然数,,中恰有一个偶数”正确的反设为( )
A.,,都是奇数 B. ,,都是偶数
C.,,中至少有两个偶数或都是奇数 D. ,,中至少有两个偶数
7. 设复数(为虚数单位),则
( )
A. B. C. D.
8.已知复数 都是实数,且),在复平面内,
Z1、Z2所对应的点与原点组成的三角形是 ( )
A.锐角三角形 B.直角三角形
C.等腰直角三角形 D.等边三角形
9.给出以下命题:
(1)若,则f(x)>0;
(2);
(3)应用微积分基本定理,有, 则F(x)=lnx;
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则;
其中正确命题的个数为 ( )
A.1 B.2 C.3 D.4
10. 由等式
定义映射( )
A、(1,2,3,4) B、(0,3,4,0)
C、 D、
二.填空题(每小题5分,共5小题,共25分)
11. 一个物体的运动方程为,其中的单位是米,的单位是秒,那么物体在2秒末的瞬时速度是___________________ 米/秒
12.化简成形式: 等于_____________
13.设,则_______________
14.如图第n个图形是由正+2边形“扩展”而来,(n=1,2,3,…)。
则第10个图形中共有________个顶点。
15.如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第99行从左至右算第67个数字为 .
三.解答题(共6小题,共75分)
16. (本题满分12分) 个男同学,个女同学站成一排,下列情况各有多少种不同排法:(1)个女同学必须排在一起;
(2)女同学从左往右按从高到低排(个女同学身高互不相等);
(3)同学甲不站在左端,同学乙不站在右端.
(注:解答须列式,答案要用数字表示)
17.(本小题满分12分)已知在的展开式中,前三项的系数成等差数列;
⑴求;
⑵求展开式中的常数项;
⑶求展开式中系数最大的项.
18..(本题满分12分) 已知曲线,
(1) 求曲线在处的切线方程;
(2) 求曲线过点(2,4)的切线方程.
19.(本小题满分12分)
已知函数在处取得极值,
(1)试求实数的值;
(2)试求函数的单调区间;
(3)若对任意,不等式恒成立,求实数的取值范围.
20. (本小题满分13分)设数列的前项和为,且对任意的都有
,
(1)求数列的前三项;
(2)猜想数列的通项公式,并用数学归纳法证明;
(3)求证:对任意都有.
21.(本小题满分14分)
如图所示,已知曲线与曲线交于点、,
直线与曲线、分别相交于点、,连结.
(Ⅰ)写出曲边四边形 (阴影部分)的面积与的函数关系式;
(Ⅱ)求函数在区间上的最大值.
杨家坪中学高2013级高二下期中考试 (理)答案
由题意,得:,∵r∈N,∴r=2或3
∴展开式中系数最大的项为.……………………………13分
19.解:(1)由题意知,∴;对求导可得:.由题意,得,即, ∴;即实数,.…………4分
20.解: (1)令得,,故; 令得,,故; 令得,,故;…………3分
(3)∵,∴,
∴
∴对任意都有.…………13分
(Ⅱ),令,即,
解得或. ……8分
,应舍去.若即时,
,.
在区间上单调递增,的最大值是. ……10分
若 即时,当时,,
当时,.在区间上单调递增,在区间上单调递减.的最大值是
. ……13分
综上所述, ……14分
17.
18.
同课章节目录
