初中数学>人教版>七年级上册>第一章 有理数>1.2 有理数1.2.4绝对值(共17张ppt)
文档属性
| 名称 | 初中数学>人教版>七年级上册>第一章 有理数>1.2 有理数1.2.4绝对值(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 627.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 18:53:57 | ||
图片预览





文档简介
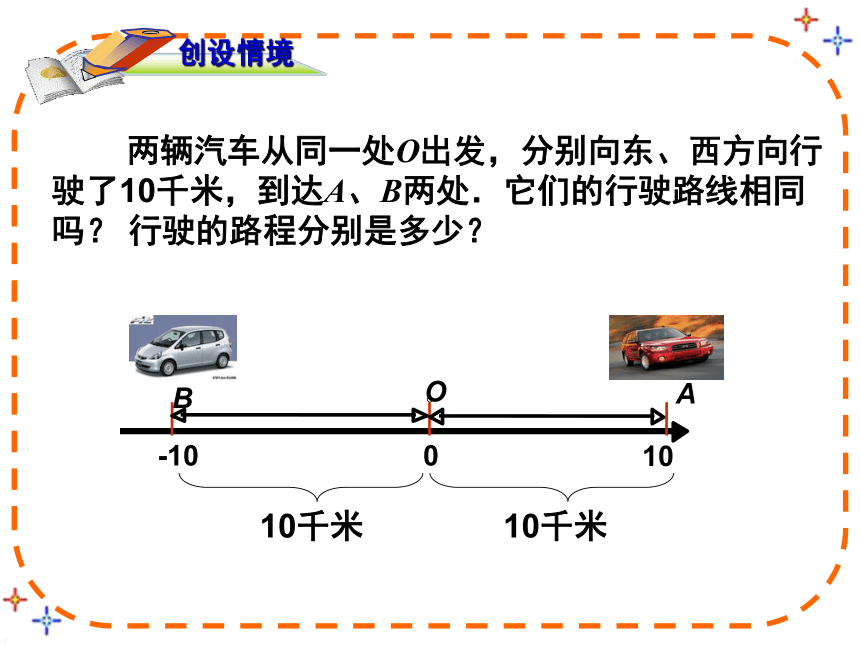
两辆汽车从同一处O出发,分别向东、西方向行
驶了10千米,到达A、B两处.它们的行驶路线相同
吗? 行驶的路程分别是多少?
创设情境
0
-10
10
O
B
A
10千米
10千米
温故知新
1.什么是正数、负数?
2.什么是有理数?按定义如何分类?按性质如何分类?
3.什么是数轴?它的三要素是什么?
4.什么是相反数?
温故知新
5.化简:
6.在数轴上表示下列各数,并用<把它们连接起来。
①-(+2); ②+(-5);
③+(+6); ④-(-100);
⑤+[(-(+2017)] ;⑥+[-(-9)];
3, -3,4,-1.5, 0,- , 。
2
3
3
4
0
1
2
3
-1
-2
-3
-4
4
5
-5
. . . . . . . . . . . . . . . . .
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
. . . . . . . . . . . . . . . . . . .
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
A
B
M
N
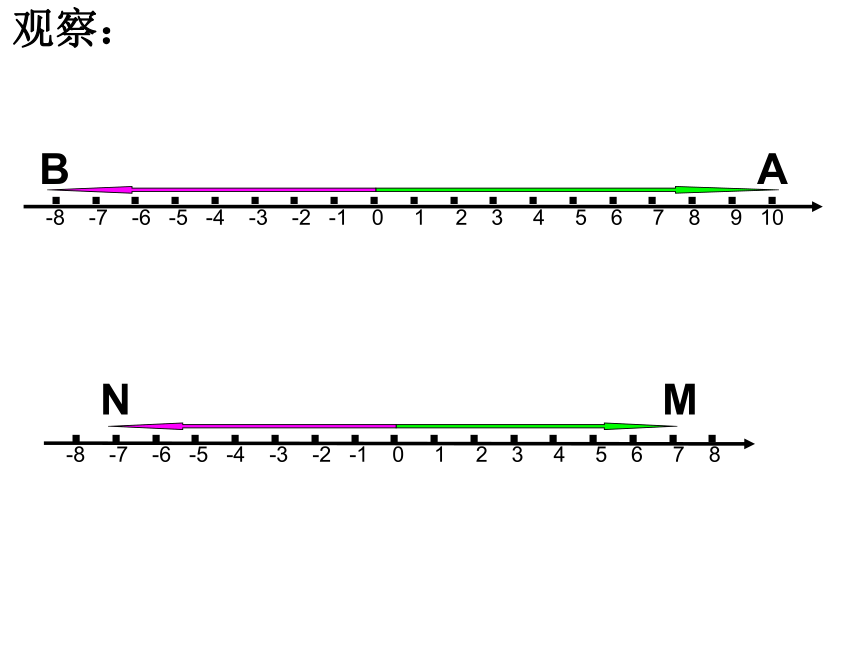
观察:
1.绝对值的定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值.
例如,+2的绝对值是2,记作| + 2| = 2;
-3的绝对值是3 ,记作|-3| = 3.
2.一般地,数轴上表示数a的点与原点的距离叫做a的绝对值,记做|a|。
绝对值的定义与记法
绝对值的性质——文字语言:
①一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零。
②互为相反数的两个数的绝对值相同。
观察思考: + 5的绝对值是5,记作|+5| = 5;
+12的绝对值是12,记作|+12| =12;
-5的绝对值是5 ,记作|-5| = 5;
-12的绝对值是12 ,记作|-12| =12;
0的绝对值是0 ,记作|0| = 0。
绝对值的性质
绝对值的性质——符号语言:
①当a>0时,︱a︱=a;
②当a<0时,︱a︱=-a;
③当a=0时,︱a︱=0。
通过大量的练习也可得到:一个正数的绝对值是一个正数,一个负数的绝对值也是一个正数,0的绝对值是0(也可以说0的绝对值是它本身; 0的绝对值是它的相反数。 )。
1.有没有绝对值等于-2的数?一个数的绝对值会是
负数吗?为什么?不论有理数 取何值,它的绝对值总
是什么数?
思 考
不论有理数a取何值,它的绝对值总是正数或0,
即对任意有理数a,总有|a|≥0.
即得一个重要的结论:
|a|是0或正数;即: |a|是一个非负数;也可以说: |a|的最小值是0。
2.互为相反数的两个数的绝对值有什么关系?
思 考
一对相反数虽然分别在原点两边,但它们
到原点的距离是相等的.所以互为相反数的两
个数的绝对值相等.
基本练习
1.填空:① |-3.2| = ;② |-4| = ;
③ |0|= ;④ +|-80| = ;
⑤ -|-16| = ;⑥ -|+2.9| = 。
2.填空:
①若|a|=3,则a= ;②若|a|=0,则a= ;③若|-a|=2,则a= ;
3.填空:
①若一个数的绝对值是它本身,则这个数是 ;
②若一个数的绝对值是它的相反数,则这个数是 。
练习1:-2的绝对值表示它离原点的距离是 个
单位,记作 .
练习2:-0.8的绝对值是 .
练习3:口答:
(1)|+6|=?????? ,| |=?????? , |8.2|=??????;
(2)|0|=?????? ;
(3)|-3|=?????? ,|- |=?????? , |-0.6|=???? .
达标练习
2
6
8.2
0
3
0.6
0.8
一个数的绝对值与这个数的关系:
1.正数的绝对值是它本身;
即当a是正数时,那么|a|=a;
2.负数的绝对值是它的相反数;
即当a是负数时,那么|a|=-a;
3.0的绝对值是0.
即当a=0,那么|a|=0
也可以说0的绝对值是它本身; 0的绝对值是它的相反数。
汇总绝对值的性质——符号语言:
①当a≥0时,︱a︱=a;
②当a≤0时,︱a︱=-a。
即:一个非负数的绝对值是它本身;一个非正数的绝对值是它的相反数。
绝对值的性质——符号语言:
①当a>0时,︱a︱=a;
②当a<0时,︱a︱=-a;
③当a=0时,︱a︱=0。
拓展练习
1.计算:
① |-18| + |-12| - |-9|
② |-4|×|-25|÷|-2|
③ |- | - |- |
1
2
1
3
拓展练习
2.若 |x-3| + |y-5|=0,求x、y的值。
3.若 |a + 3| + |b-2|=0,求a、b的值。
解:∵|x-3| ≥0 |y-5|≥0
|x-3| + |y-5|=0
∴ x-3 =0 y-5=0
∴ |x-3|=0 |y-5|=0
∴ x =3 y=5
再 见
驶了10千米,到达A、B两处.它们的行驶路线相同
吗? 行驶的路程分别是多少?
创设情境
0
-10
10
O
B
A
10千米
10千米
温故知新
1.什么是正数、负数?
2.什么是有理数?按定义如何分类?按性质如何分类?
3.什么是数轴?它的三要素是什么?
4.什么是相反数?
温故知新
5.化简:
6.在数轴上表示下列各数,并用<把它们连接起来。
①-(+2); ②+(-5);
③+(+6); ④-(-100);
⑤+[(-(+2017)] ;⑥+[-(-9)];
3, -3,4,-1.5, 0,- , 。
2
3
3
4
0
1
2
3
-1
-2
-3
-4
4
5
-5
. . . . . . . . . . . . . . . . .
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
. . . . . . . . . . . . . . . . . . .
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
A
B
M
N
观察:
1.绝对值的定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值.
例如,+2的绝对值是2,记作| + 2| = 2;
-3的绝对值是3 ,记作|-3| = 3.
2.一般地,数轴上表示数a的点与原点的距离叫做a的绝对值,记做|a|。
绝对值的定义与记法
绝对值的性质——文字语言:
①一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零。
②互为相反数的两个数的绝对值相同。
观察思考: + 5的绝对值是5,记作|+5| = 5;
+12的绝对值是12,记作|+12| =12;
-5的绝对值是5 ,记作|-5| = 5;
-12的绝对值是12 ,记作|-12| =12;
0的绝对值是0 ,记作|0| = 0。
绝对值的性质
绝对值的性质——符号语言:
①当a>0时,︱a︱=a;
②当a<0时,︱a︱=-a;
③当a=0时,︱a︱=0。
通过大量的练习也可得到:一个正数的绝对值是一个正数,一个负数的绝对值也是一个正数,0的绝对值是0(也可以说0的绝对值是它本身; 0的绝对值是它的相反数。 )。
1.有没有绝对值等于-2的数?一个数的绝对值会是
负数吗?为什么?不论有理数 取何值,它的绝对值总
是什么数?
思 考
不论有理数a取何值,它的绝对值总是正数或0,
即对任意有理数a,总有|a|≥0.
即得一个重要的结论:
|a|是0或正数;即: |a|是一个非负数;也可以说: |a|的最小值是0。
2.互为相反数的两个数的绝对值有什么关系?
思 考
一对相反数虽然分别在原点两边,但它们
到原点的距离是相等的.所以互为相反数的两
个数的绝对值相等.
基本练习
1.填空:① |-3.2| = ;② |-4| = ;
③ |0|= ;④ +|-80| = ;
⑤ -|-16| = ;⑥ -|+2.9| = 。
2.填空:
①若|a|=3,则a= ;②若|a|=0,则a= ;③若|-a|=2,则a= ;
3.填空:
①若一个数的绝对值是它本身,则这个数是 ;
②若一个数的绝对值是它的相反数,则这个数是 。
练习1:-2的绝对值表示它离原点的距离是 个
单位,记作 .
练习2:-0.8的绝对值是 .
练习3:口答:
(1)|+6|=?????? ,| |=?????? , |8.2|=??????;
(2)|0|=?????? ;
(3)|-3|=?????? ,|- |=?????? , |-0.6|=???? .
达标练习
2
6
8.2
0
3
0.6
0.8
一个数的绝对值与这个数的关系:
1.正数的绝对值是它本身;
即当a是正数时,那么|a|=a;
2.负数的绝对值是它的相反数;
即当a是负数时,那么|a|=-a;
3.0的绝对值是0.
即当a=0,那么|a|=0
也可以说0的绝对值是它本身; 0的绝对值是它的相反数。
汇总绝对值的性质——符号语言:
①当a≥0时,︱a︱=a;
②当a≤0时,︱a︱=-a。
即:一个非负数的绝对值是它本身;一个非正数的绝对值是它的相反数。
绝对值的性质——符号语言:
①当a>0时,︱a︱=a;
②当a<0时,︱a︱=-a;
③当a=0时,︱a︱=0。
拓展练习
1.计算:
① |-18| + |-12| - |-9|
② |-4|×|-25|÷|-2|
③ |- | - |- |
1
2
1
3
拓展练习
2.若 |x-3| + |y-5|=0,求x、y的值。
3.若 |a + 3| + |b-2|=0,求a、b的值。
解:∵|x-3| ≥0 |y-5|≥0
|x-3| + |y-5|=0
∴ x-3 =0 y-5=0
∴ |x-3|=0 |y-5|=0
∴ x =3 y=5
再 见
