人教版数学七上1.3.1有理数的加法ppt课件(共20张ppt)
文档属性
| 名称 | 人教版数学七上1.3.1有理数的加法ppt课件(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 19:19:37 | ||
图片预览







文档简介
9+10=( )
(-9)+(-10)=( )
(-9)+10=( )
(-10)+9=( )
通过预习,以上题目你能够独立完成吗?更多这样的题目是否能独立完成?你能不能归纳解题的步骤?
(-10)+10=( )
(-10)+0=( )
例1 计算:
(1)(-3)+(-9)= -(3+9)
= -12
(2)(-4.7)+ 3.9 = -(4.7-3.9)
= -0.8
(1)(-3)+(-9) (2)(-4.7)+3.9
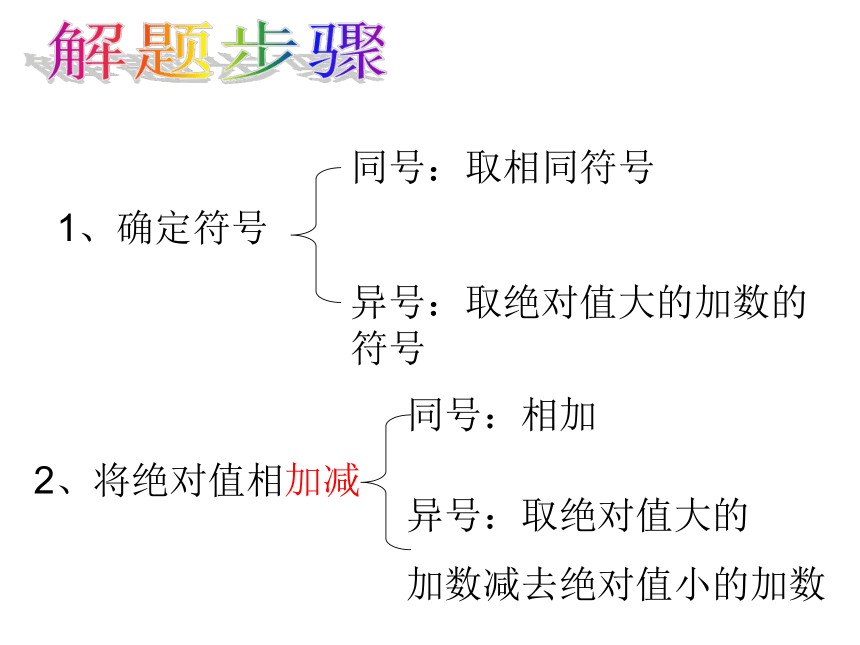
1、确定符号
同号:取相同符号
异号:取绝对值大的加数的符号
2、将绝对值相加减
同号:相加
异号:取绝对值大的
加数减去绝对值小的加数
1、同号两数相加,取相同的符号,并把绝对值相加;
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0;
3、一个数同0相加,仍得这个数。
(1)(-2012)+0
(2)(-3)+(-12)
解:原式=-(2012-0)确定符号
=-2012 绝对值相减
解:原式=-(3+12)确定符号
=-15 绝对值相加
(1)(-1.25)+1.75
(2)(-8)+20
解:原式=+(1.75-1.25)确定符号
=0.5 绝对值相减
解:原式=+(20-8)确定符号
=12 绝对值相减
(1)如果物体先向右运动5m,再向右运动3m,那么两次运动后总的结果是什么?
0
5
8
如图,对于上面的这种情况,我们把原地看成原点,用数学来表示就是
5 + 3 = 8
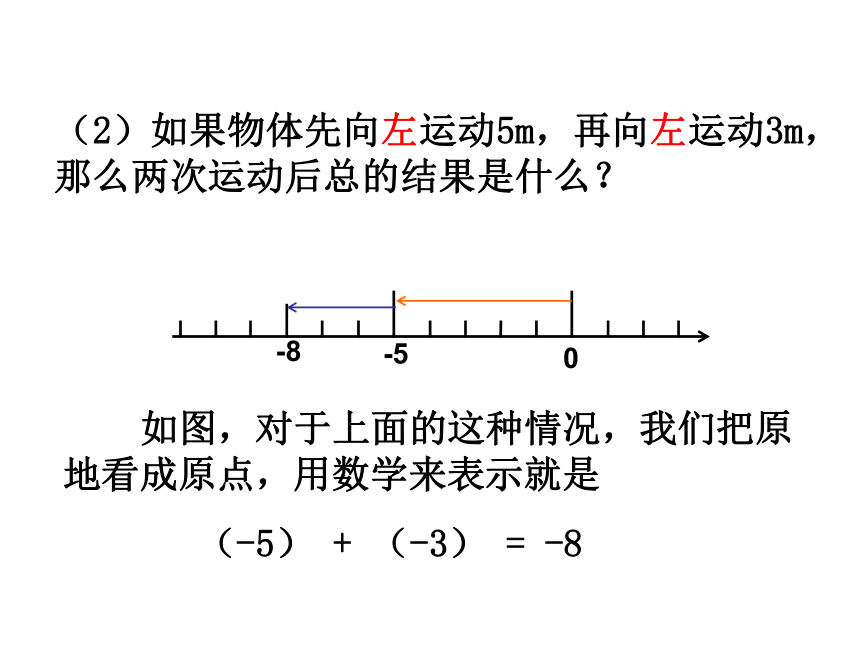
(2)如果物体先向左运动5m,再向左运动3m,那么两次运动后总的结果是什么?
0
-5
-8
如图,对于上面的这种情况,我们把原地看成原点,用数学来表示就是
(-5) + (-3) = -8
(3)如果物体先向右运动5m,再向左运动 3m,那么两次运动后总的结果是什么?
如图,对于上面的这种情况,我们把原地看成原点,用数学来表示就是
5 + (-3) = 2
0
5
2
利用数轴,求以下情况时物体两次运动的结果:
(1)先向右运动3m,再向左运动5m,物体从起点向 运动了 m
(2)先向右运动5m,再向左运动5m,物体从起点向 运动了 m
(3)先向左运动5m,再向右运动5m,物体从起点向 运动了 m
左
0
左或右
左或右
0
2
例2 足球循环赛中,红队胜黄队4:1,黄队 胜红队1:0,计算各队的净胜球数.
解:三场比赛中,红队共进4球,失2球,净胜球数为(+4)+(-2)=+(4-2)=2;
黄队共进2球,失4球,净胜球数为
(+2)+(-4)= -(4-2)= -2;
蓝队共进1球,失1球,净胜球数为
(+1)+(-1)=0
在有理数运算中,以前的加法运算律通用,如:
加法交换律:a+b=b+a
30+(-20)=(-20)+30
加法结合律: (a+b)+c=a+(b+c)
[8+(-5)]+(-4)=8+[(-5)+(-4)]
1、 计算:16+(-25)+24+(-35)
解:16+(-25)+24+(-35)
=16+24+(-25)+(-35)
=40+(-60)
=-20
2、每袋小麦的标准重量为90千克,10袋小麦称重记录如下:
91,91,91.5,89,91.2,91.3,88.7,
88.8,91.8,91.1,
与标准重量比较,10袋小麦总计 超过多少千克或不足多少千克? 10袋小麦的总重量是多少?
解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7
+88.8+91.8+91.1=905.4
再计算总计超过多少千克
905.4-90×10=5.4
解法2:每袋小麦超过标准重量的千克数记作正
数,不足的千克数记作负数.
10袋小麦对应的数为
+1,+1,+1.5,-1,+1.2,+1.3,
-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)] +(1+1.5+1.8+1.1)
=5.4.
90×10+5.4=905.4.
三个以上有理数相加,
(1)先将其中的相反数相加;
(2)再将正数,负数分别相加;
(3)若有同分母的分数或相加得整数
的先相加;
(4)最后求出异号加数的和.
1.判断题:
(1)两个负数的和一定是负数;
(2)绝对值相等的两个数的和等于零;
(3)若两个有理数相加时的和为负数,这两个有理数一定都是负数;
(4)若两个有理数相加时的和为正数,这两个有理数一定都是正数。
2.已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值。
3.计算:
(1)(-7)+ 11 + 3 +(-2);
(2)
4.绝对值不大于10的整数有( )个,它们的和是 ( ).
5、填空:
(1)若a>0,b>0,那么a+b 0.
(2)若a<0,b<0,那么a+b 0.
(3)若a>0,b<0,且│a│>│b│那
么a+b 0.
(4)若a<0,b>0,且│a│>│b│那
么a+b 0.
(-9)+(-10)=( )
(-9)+10=( )
(-10)+9=( )
通过预习,以上题目你能够独立完成吗?更多这样的题目是否能独立完成?你能不能归纳解题的步骤?
(-10)+10=( )
(-10)+0=( )
例1 计算:
(1)(-3)+(-9)= -(3+9)
= -12
(2)(-4.7)+ 3.9 = -(4.7-3.9)
= -0.8
(1)(-3)+(-9) (2)(-4.7)+3.9
1、确定符号
同号:取相同符号
异号:取绝对值大的加数的符号
2、将绝对值相加减
同号:相加
异号:取绝对值大的
加数减去绝对值小的加数
1、同号两数相加,取相同的符号,并把绝对值相加;
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0;
3、一个数同0相加,仍得这个数。
(1)(-2012)+0
(2)(-3)+(-12)
解:原式=-(2012-0)确定符号
=-2012 绝对值相减
解:原式=-(3+12)确定符号
=-15 绝对值相加
(1)(-1.25)+1.75
(2)(-8)+20
解:原式=+(1.75-1.25)确定符号
=0.5 绝对值相减
解:原式=+(20-8)确定符号
=12 绝对值相减
(1)如果物体先向右运动5m,再向右运动3m,那么两次运动后总的结果是什么?
0
5
8
如图,对于上面的这种情况,我们把原地看成原点,用数学来表示就是
5 + 3 = 8
(2)如果物体先向左运动5m,再向左运动3m,那么两次运动后总的结果是什么?
0
-5
-8
如图,对于上面的这种情况,我们把原地看成原点,用数学来表示就是
(-5) + (-3) = -8
(3)如果物体先向右运动5m,再向左运动 3m,那么两次运动后总的结果是什么?
如图,对于上面的这种情况,我们把原地看成原点,用数学来表示就是
5 + (-3) = 2
0
5
2
利用数轴,求以下情况时物体两次运动的结果:
(1)先向右运动3m,再向左运动5m,物体从起点向 运动了 m
(2)先向右运动5m,再向左运动5m,物体从起点向 运动了 m
(3)先向左运动5m,再向右运动5m,物体从起点向 运动了 m
左
0
左或右
左或右
0
2
例2 足球循环赛中,红队胜黄队4:1,黄队 胜红队1:0,计算各队的净胜球数.
解:三场比赛中,红队共进4球,失2球,净胜球数为(+4)+(-2)=+(4-2)=2;
黄队共进2球,失4球,净胜球数为
(+2)+(-4)= -(4-2)= -2;
蓝队共进1球,失1球,净胜球数为
(+1)+(-1)=0
在有理数运算中,以前的加法运算律通用,如:
加法交换律:a+b=b+a
30+(-20)=(-20)+30
加法结合律: (a+b)+c=a+(b+c)
[8+(-5)]+(-4)=8+[(-5)+(-4)]
1、 计算:16+(-25)+24+(-35)
解:16+(-25)+24+(-35)
=16+24+(-25)+(-35)
=40+(-60)
=-20
2、每袋小麦的标准重量为90千克,10袋小麦称重记录如下:
91,91,91.5,89,91.2,91.3,88.7,
88.8,91.8,91.1,
与标准重量比较,10袋小麦总计 超过多少千克或不足多少千克? 10袋小麦的总重量是多少?
解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7
+88.8+91.8+91.1=905.4
再计算总计超过多少千克
905.4-90×10=5.4
解法2:每袋小麦超过标准重量的千克数记作正
数,不足的千克数记作负数.
10袋小麦对应的数为
+1,+1,+1.5,-1,+1.2,+1.3,
-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)] +(1+1.5+1.8+1.1)
=5.4.
90×10+5.4=905.4.
三个以上有理数相加,
(1)先将其中的相反数相加;
(2)再将正数,负数分别相加;
(3)若有同分母的分数或相加得整数
的先相加;
(4)最后求出异号加数的和.
1.判断题:
(1)两个负数的和一定是负数;
(2)绝对值相等的两个数的和等于零;
(3)若两个有理数相加时的和为负数,这两个有理数一定都是负数;
(4)若两个有理数相加时的和为正数,这两个有理数一定都是正数。
2.已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值。
3.计算:
(1)(-7)+ 11 + 3 +(-2);
(2)
4.绝对值不大于10的整数有( )个,它们的和是 ( ).
5、填空:
(1)若a>0,b>0,那么a+b 0.
(2)若a<0,b<0,那么a+b 0.
(3)若a>0,b<0,且│a│>│b│那
么a+b 0.
(4)若a<0,b>0,且│a│>│b│那
么a+b 0.
