人教版七年级上册1.4.1.1 有理数的乘法课件(15张PPT)
文档属性
| 名称 | 人教版七年级上册1.4.1.1 有理数的乘法课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 479.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览





文档简介
《数学》(七年级 上册)
水库水位的变化
水库水位的变化
探 究
有理数的乘法法则
两数相乘,同号得 ,异号得 ,并把绝对值相乘;任何数同0相乘,都得0.
例 题 解 析
例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)
倒 数 的 定 义
由例 1 的 (3) 、(4)的求解:
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
几个有理数相乘,因数都不为 0 时,
积的符号由 确定:
算一算
看谁说得快
用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.
? 小结 ? 思考 ?
1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?
谢谢!
第一章 有理数及其运算
甲水库
第一天
乙水库
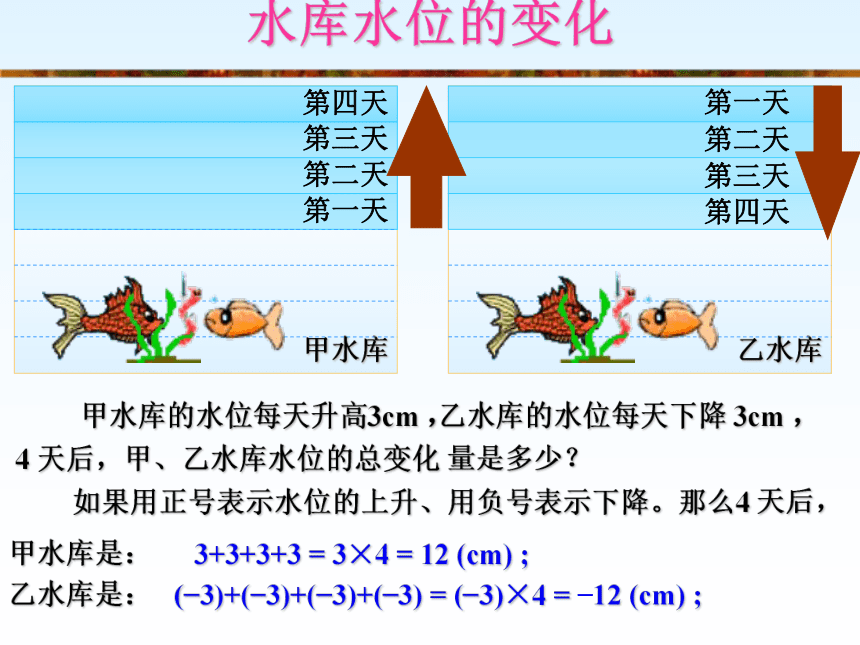
甲水库的水位每天升高3cm ,
第二天
第三天
第四天
乙水库的水位每天下降 3cm ,
第一天
第二天
第三天
第四天
4 天后,甲、乙水库水位的总变化 量是多少?
如果用正号表示水位的上升、用负号表示下降。那么4 天后,
甲水库是:
乙水库是:
3+3+3+3 = 3×4 = 12 (cm) ;
(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12 (cm) ;
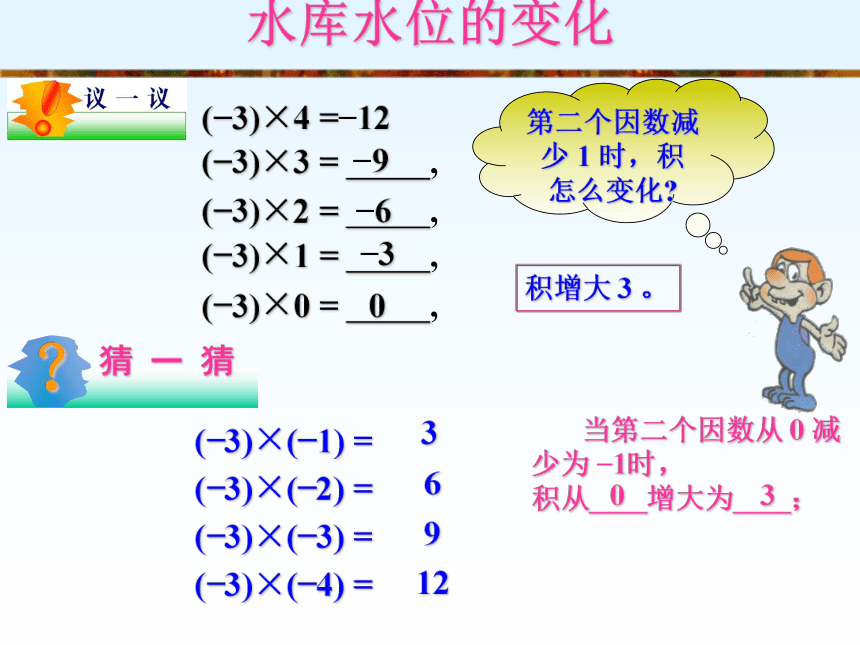
(?3)×4 =?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) =
(?3)×(?2) =
(?3)×(?3) =
(?3)×(?4) =
第二个因数减少 1 时,积 怎么变化?
3
6
9
12
当第二个因数从 0 减少为 ?1时,
积从 增大为 ;
积增大 3 。
0
3
猜 一 猜
?
(?3)×4 = ?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) =
(?3)×(?2) =
(?3)×(?3) =
(?3)×(?4) =
3
6
9
12
由上述所列各式 , 你能看出两有理数相乘与它们的积之间的规律吗?
归纳 ?
负数乘正数得负,
绝对值相乘;
负数乘 0 得 0 ;
负数乘负数得正,
绝对值相乘;
试用简练的语言叙述上面得出的结论。
正
负
? ?思考 ?
怎样利用法则来进行两有理数的乘法运算与得出结果的?
解:(1) (?4)×5 (2) (?4)×(?7)
=?(4×5) =+(4×7)
=?20 ; =35;
(3) (4)
=1 ;
=1 ;
求解中的第一步是 ;
确定积的符号
第二步
是 ;
绝对值相乘
? 解题后的反思 ?
(3) (4)
=1;
=1 ;
可知
我们把
三个有理数相乘,你会计算吗?
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
方法提示
三个有理数相乘,先把前两个相乘,
再把
所得结果与另一数相乘。
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
教材对本例的求解,是连续两次使用乘法法则。
(2)
=?1 .
? 解题后的反思 ?
如果我们把乘法法则推广到三个有理数相乘,只“一次性地”先定号再绝对值相乘,
解:(1) (?4)×5 ×(?0.25) (2)
=+(4×5×0.25)
几个有理数相乘,因数都不为 0 时,
积的符号怎样确定?
-
有一因数为 0 时,积是多少?
负因数的个数
奇数个为负,偶数个为正。
有一因数为 0 时,积是
0 。
1、写出下列各数的倒数
15
5
9
0.25
解:
4
1
4
(1)
(3)
(2)
(4)
的倒数是
(1)
15
15
1
5
9
(2)
的倒数是
9
5
0.25
(3)
的倒数是
4
的倒数是
4
1
4
(4)
17
4
(1)
( 8)
×
( 7)
(2)
2.9
×
( 0.4)
(3)
×
8
9
1
4
(4)
100
×
( 0.001)
(5)
×
3
( 2)
×
( 4)
(6)
×
7
( 6)
×
( 5)
<
<
>
>
=
《数学》(七年级 上册)
水库水位的变化
水库水位的变化
探 究
有理数的乘法法则
两数相乘,同号得 ,异号得 ,并把绝对值相乘;任何数同0相乘,都得0.
例 题 解 析
例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)
倒 数 的 定 义
由例 1 的 (3) 、(4)的求解:
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
几个有理数相乘,因数都不为 0 时,
积的符号由 确定:
算一算
看谁说得快
用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.
? 小结 ? 思考 ?
1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?
谢谢!
水库水位的变化
水库水位的变化
探 究
有理数的乘法法则
两数相乘,同号得 ,异号得 ,并把绝对值相乘;任何数同0相乘,都得0.
例 题 解 析
例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)
倒 数 的 定 义
由例 1 的 (3) 、(4)的求解:
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
几个有理数相乘,因数都不为 0 时,
积的符号由 确定:
算一算
看谁说得快
用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.
? 小结 ? 思考 ?
1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?
谢谢!
第一章 有理数及其运算
甲水库
第一天
乙水库
甲水库的水位每天升高3cm ,
第二天
第三天
第四天
乙水库的水位每天下降 3cm ,
第一天
第二天
第三天
第四天
4 天后,甲、乙水库水位的总变化 量是多少?
如果用正号表示水位的上升、用负号表示下降。那么4 天后,
甲水库是:
乙水库是:
3+3+3+3 = 3×4 = 12 (cm) ;
(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12 (cm) ;
(?3)×4 =?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) =
(?3)×(?2) =
(?3)×(?3) =
(?3)×(?4) =
第二个因数减少 1 时,积 怎么变化?
3
6
9
12
当第二个因数从 0 减少为 ?1时,
积从 增大为 ;
积增大 3 。
0
3
猜 一 猜
?
(?3)×4 = ?12
(?3)×3 = ,
(?3)×2 = ,
(?3)×1 = ,
(?3)×0 = ,
?9
?6
?3
0
(?3)×(?1) =
(?3)×(?2) =
(?3)×(?3) =
(?3)×(?4) =
3
6
9
12
由上述所列各式 , 你能看出两有理数相乘与它们的积之间的规律吗?
归纳 ?
负数乘正数得负,
绝对值相乘;
负数乘 0 得 0 ;
负数乘负数得正,
绝对值相乘;
试用简练的语言叙述上面得出的结论。
正
负
? ?思考 ?
怎样利用法则来进行两有理数的乘法运算与得出结果的?
解:(1) (?4)×5 (2) (?4)×(?7)
=?(4×5) =+(4×7)
=?20 ; =35;
(3) (4)
=1 ;
=1 ;
求解中的第一步是 ;
确定积的符号
第二步
是 ;
绝对值相乘
? 解题后的反思 ?
(3) (4)
=1;
=1 ;
可知
我们把
三个有理数相乘,你会计算吗?
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
方法提示
三个有理数相乘,先把前两个相乘,
再把
所得结果与另一数相乘。
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25)
=+(20×0.25)
=5.
=(?20)×(?0.25)
教材对本例的求解,是连续两次使用乘法法则。
(2)
=?1 .
? 解题后的反思 ?
如果我们把乘法法则推广到三个有理数相乘,只“一次性地”先定号再绝对值相乘,
解:(1) (?4)×5 ×(?0.25) (2)
=+(4×5×0.25)
几个有理数相乘,因数都不为 0 时,
积的符号怎样确定?
-
有一因数为 0 时,积是多少?
负因数的个数
奇数个为负,偶数个为正。
有一因数为 0 时,积是
0 。
1、写出下列各数的倒数
15
5
9
0.25
解:
4
1
4
(1)
(3)
(2)
(4)
的倒数是
(1)
15
15
1
5
9
(2)
的倒数是
9
5
0.25
(3)
的倒数是
4
的倒数是
4
1
4
(4)
17
4
(1)
( 8)
×
( 7)
(2)
2.9
×
( 0.4)
(3)
×
8
9
1
4
(4)
100
×
( 0.001)
(5)
×
3
( 2)
×
( 4)
(6)
×
7
( 6)
×
( 5)
<
<
>
>
=
《数学》(七年级 上册)
水库水位的变化
水库水位的变化
探 究
有理数的乘法法则
两数相乘,同号得 ,异号得 ,并把绝对值相乘;任何数同0相乘,都得0.
例 题 解 析
例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)
倒 数 的 定 义
由例 1 的 (3) 、(4)的求解:
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
例 题 解 析
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
例2 计算:
(1) (?4)×5×(?0.25); (2)
乘积 的符号 的确定
几个有理数相乘,因数都不为 0 时,
积的符号由 确定:
算一算
看谁说得快
用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.
? 小结 ? 思考 ?
1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?
谢谢!
