2.2 30°、45°、60°角的三角函数值课件(共21张PPT)
文档属性
| 名称 | 2.2 30°、45°、60°角的三角函数值课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 23:28:54 | ||
图片预览







文档简介
第二章 直角三角形的边角关系
2 30°、45°、60°角的三角函数值
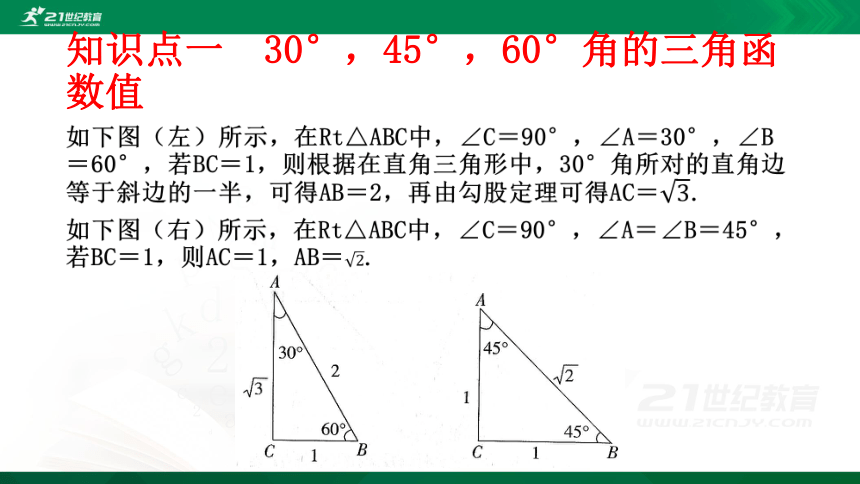
知识点一 30°,45°,60°角的三角函数值
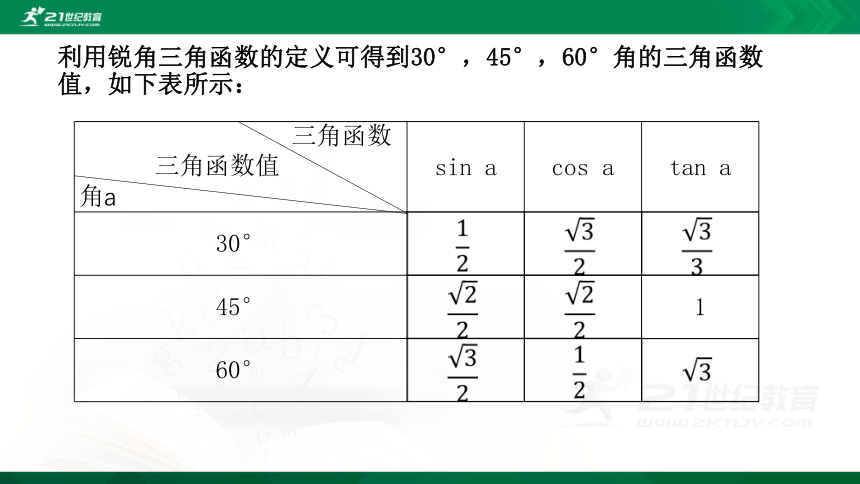
利用锐角三角函数的定义可得到30°,45°,60°角的三角函数值,如下表所示:
规律总结
知识点二 30°,45°,60°角的三角函数值的应用
有些实际问题通过分析题意建立数学模型后,可转化为含有特殊角的直角三角形问题,从而利用特殊角的三角函数值解决问题.
例2 下图是某商场营业大厅自动扶梯示意图自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A,C之间的距离为4m,则自动扶梯的垂直高度BD=_______m.(结果保留根号)
答案 2
解析 ∵∠BCD=∠BAC+∠ABC,∠BAC=30°,∠BCD=60°,∴∠ABC=∠BCD-∠BAC=30°. ∴∠BAC=∠ABC.∴BC=AC=4m.在Rt△BDC中,sin∠BCD=,∴sin60°= , ∴BD=2(m),即自动扶梯的垂直高度BD=2m.
方法技巧 解决此题的技巧有两点:一是发现含有特殊角的直角三角形;二是发现60°与30°的倍数关系,得到△CBA为等腰三角形,从而使问题巧妙解决.
知识点二 30°,45°,60°角的三角函数值的应用
有些实际问题通过分析题意建立数学模型后,可转化为含有特殊角的直角三角形问题,从而利用特殊角的三角函数值解决问题.
例2 下图是某商场营业大厅自动扶梯示意图自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A,C之间的距离为4m,则自动扶梯的垂直高度BD=_______m.(结果保留根号)
经典例题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型二 15°,75°等特殊角的三角函数值的有关计算
例2 如图所示,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算:tan15°=_________.
2 30°、45°、60°角的三角函数值
知识点一 30°,45°,60°角的三角函数值
利用锐角三角函数的定义可得到30°,45°,60°角的三角函数值,如下表所示:
规律总结
知识点二 30°,45°,60°角的三角函数值的应用
有些实际问题通过分析题意建立数学模型后,可转化为含有特殊角的直角三角形问题,从而利用特殊角的三角函数值解决问题.
例2 下图是某商场营业大厅自动扶梯示意图自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A,C之间的距离为4m,则自动扶梯的垂直高度BD=_______m.(结果保留根号)
答案 2
解析 ∵∠BCD=∠BAC+∠ABC,∠BAC=30°,∠BCD=60°,∴∠ABC=∠BCD-∠BAC=30°. ∴∠BAC=∠ABC.∴BC=AC=4m.在Rt△BDC中,sin∠BCD=,∴sin60°= , ∴BD=2(m),即自动扶梯的垂直高度BD=2m.
方法技巧 解决此题的技巧有两点:一是发现含有特殊角的直角三角形;二是发现60°与30°的倍数关系,得到△CBA为等腰三角形,从而使问题巧妙解决.
知识点二 30°,45°,60°角的三角函数值的应用
有些实际问题通过分析题意建立数学模型后,可转化为含有特殊角的直角三角形问题,从而利用特殊角的三角函数值解决问题.
例2 下图是某商场营业大厅自动扶梯示意图自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°,A,C之间的距离为4m,则自动扶梯的垂直高度BD=_______m.(结果保留根号)
经典例题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型一 有关30°,45°,60°角的三角函数值的综合题
题型二 15°,75°等特殊角的三角函数值的有关计算
例2 如图所示,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算:tan15°=_________.
