21.2.1二次根式的乘法 同步练习 -2021-2022学年九年级数学华东师大版上册(word版含解析)
文档属性
| 名称 | 21.2.1二次根式的乘法 同步练习 -2021-2022学年九年级数学华东师大版上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 248.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 18:20:37 | ||
图片预览



文档简介
21.2.1二次根式的乘法
一、单选题
1.计算的结果等于(
)
A.
B.
C.
D.
2.下列各式计算正确的是( )
A.
B.
C.
D.
3.下列各式中是最简二次根式的是(
)
A.
B.
C.
D.
4.估计的运算结果在哪两个整数之间(
)
A.1和2
B.2和3
C.3和4
D.4和5
5.一矩形的长为,宽为,则该矩形的面积为(
)
A.
B.3
C.
D.
6.估计×的值应在(
)
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
7.将化为最简二次根式,其结果是(
)
A.
B.
C.
D.
8.下列实数中,有理数是(
)
A.
B.
C.
D.
9.已知一直角三角形,三边的平方和为,则斜边长为(
)
A.
B.
C.
D.不能确定
10.我们把形如a+b(a,b为有理数,为最简二次根式)的数叫做型无理数,如3+1是型无理数,则是( )
A.型无理数
B.型无理数
C.型无理数
D.型无理数
二、填空题
11.的小数部分为a,则____________.
12.计算的结果是__________.
13.化简的结果是______.
14.计算:的结果是____________.
15.已知,则__________.
三、解答题
16.已知:
(1)求和的值
(2)若,求x的值
(3)若,求a的值
17.已知a,b分别是4+的整数部分和小数部分.
(1)分别写出a,b的值;
(2)求b2+2a的值.
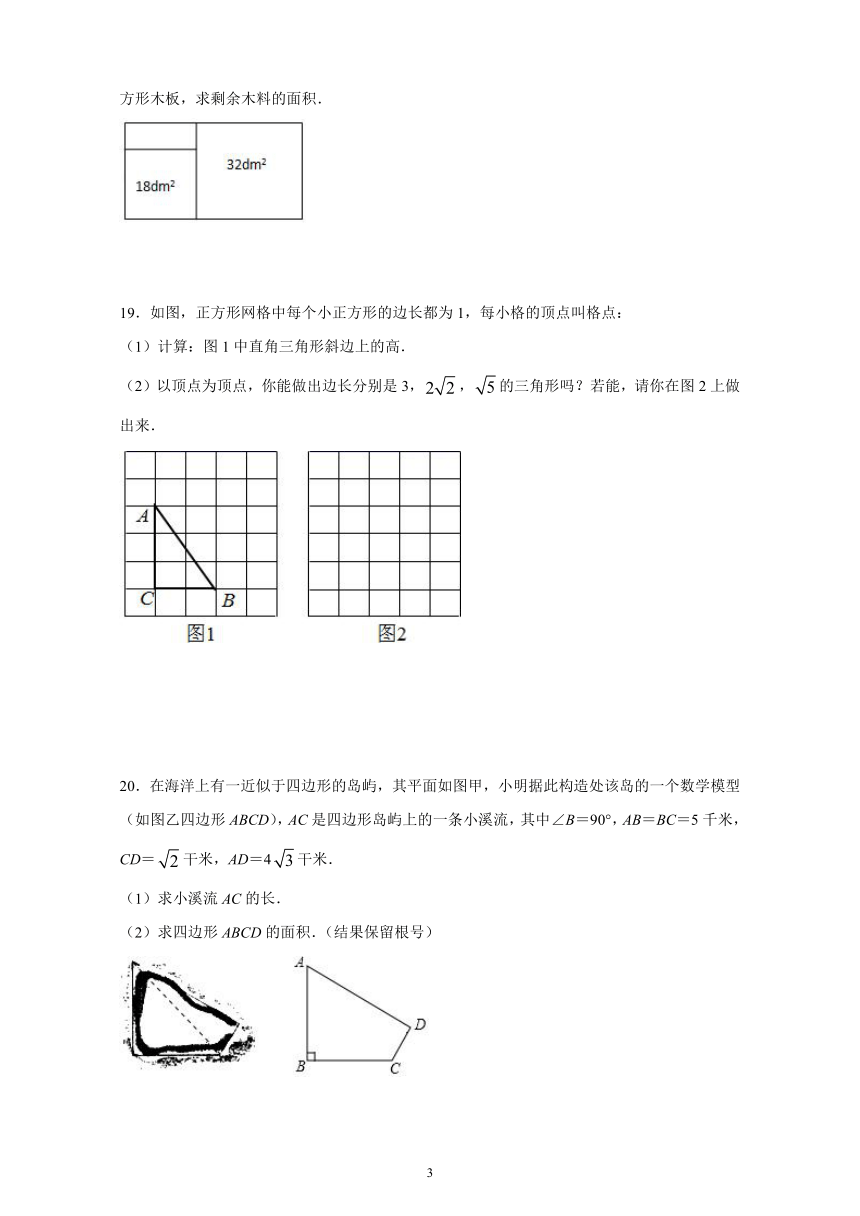
18.有一块矩形木块,木工采用如图方式,求木板上截出两个面积分别为18dm2和32dm2的正方形木板,求剩余木料的面积.
19.如图,正方形网格中每个小正方形的边长都为1,每小格的顶点叫格点:
(1)计算:图1中直角三角形斜边上的高.
(2)以顶点为顶点,你能做出边长分别是3,,的三角形吗?若能,请你在图2上做出来.
20.在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,CD=干米,AD=4干米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
参考答案
1.C
解:
故选:C.
2.C
解:(A)=2,是4的算术平方根,为正2,故A错;
(B)由平方差公式,可得:=3,正确.
(C)=2,故错;
(D)、没有意义,故错;
选C.
3.A
解:A、是最简二次根式,此项符合题意;
B、,不是最简二次根式,此项不符题意;
C、,不是最简二次根式,此项不符题意;
D、,不是最简二次根式,此项不符题意.
故选:A.
4.D
解:原式,
,
,
,
故选:D.
5.D
解:;
故选:D
6.C
解:
故选C.
7.D
解:原式,
,
故选:D.
8.C
解:
A、∵是无理数,故是无理数
B、∵是无理数,故是无理数
C、为有理数
D、∵是无理数,故是无理数
故选:C
9.A
解:设直角三角形的两条直角边分别为a、b,斜边为c.
根据题意,得,.
∵,
∴.
∴.
∵c>0,
∴.
故选:A
10.B
解:,
所以是型无理数,
故选:B.
11.7
解:∵的小数部分为a,4<<5,
∴a=-4,
∴.
故答案为7
12.5
解:=5.
故答案为:5.
13..
解:根据题意得>0,
∴b>0,
∴原式=
=.
故答案为.
14.2
解:原式=,
故答案为:2.
15.2
解:∵,
∴,
∴,
∴n=2.
故填:2.
16.(1),;(2)x=0.236;(3)a=2.36.
解:(1),
;
(2)∵,
故x=0.236;
(3)由
可得,
即,
故a=2.36.
17.(1)a=5,b=﹣1;(2)b2+2a=14﹣2.
解:(1)∵1<<2,
∴5<4+<6,
∴a=5,b=﹣1;
(2)∵a=5,b=﹣1,
∴b2+2a=(-1)2+2×5=4﹣2+10=14﹣2.
18.
解:∵两个正方形木板的面积分别为18dm2和32dm2,
∴这两个正方形的边长分别为:=3(dm),=4(dm),
∴剩余木料的面积为:(4﹣3)×3=×3=6(dm2).
19.(1);(2)能,见解析
解:(1)设斜边上的高为h,
根据勾股定理:AB2=AC2+BC2;
∴,;
∴.
解得;
(2)能,作图如下:
20.(1)5千米;(2)(+2)平方千米.
解:(1)如图,连接AC,∵∠B=90,AB=BC=5千米,
∴AC===5(千米);
(2)∵AC2=(5)2=50,CD2+AD2=()2+(4)2=50,
∴AC2=CD2+AD2,
则∠D=90,
S四边形ABCD=S△ABC+S△ACD
=×5×5+××4
=(+2)平方千米.
一、单选题
1.计算的结果等于(
)
A.
B.
C.
D.
2.下列各式计算正确的是( )
A.
B.
C.
D.
3.下列各式中是最简二次根式的是(
)
A.
B.
C.
D.
4.估计的运算结果在哪两个整数之间(
)
A.1和2
B.2和3
C.3和4
D.4和5
5.一矩形的长为,宽为,则该矩形的面积为(
)
A.
B.3
C.
D.
6.估计×的值应在(
)
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
7.将化为最简二次根式,其结果是(
)
A.
B.
C.
D.
8.下列实数中,有理数是(
)
A.
B.
C.
D.
9.已知一直角三角形,三边的平方和为,则斜边长为(
)
A.
B.
C.
D.不能确定
10.我们把形如a+b(a,b为有理数,为最简二次根式)的数叫做型无理数,如3+1是型无理数,则是( )
A.型无理数
B.型无理数
C.型无理数
D.型无理数
二、填空题
11.的小数部分为a,则____________.
12.计算的结果是__________.
13.化简的结果是______.
14.计算:的结果是____________.
15.已知,则__________.
三、解答题
16.已知:
(1)求和的值
(2)若,求x的值
(3)若,求a的值
17.已知a,b分别是4+的整数部分和小数部分.
(1)分别写出a,b的值;
(2)求b2+2a的值.
18.有一块矩形木块,木工采用如图方式,求木板上截出两个面积分别为18dm2和32dm2的正方形木板,求剩余木料的面积.
19.如图,正方形网格中每个小正方形的边长都为1,每小格的顶点叫格点:
(1)计算:图1中直角三角形斜边上的高.
(2)以顶点为顶点,你能做出边长分别是3,,的三角形吗?若能,请你在图2上做出来.
20.在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,CD=干米,AD=4干米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
参考答案
1.C
解:
故选:C.
2.C
解:(A)=2,是4的算术平方根,为正2,故A错;
(B)由平方差公式,可得:=3,正确.
(C)=2,故错;
(D)、没有意义,故错;
选C.
3.A
解:A、是最简二次根式,此项符合题意;
B、,不是最简二次根式,此项不符题意;
C、,不是最简二次根式,此项不符题意;
D、,不是最简二次根式,此项不符题意.
故选:A.
4.D
解:原式,
,
,
,
故选:D.
5.D
解:;
故选:D
6.C
解:
故选C.
7.D
解:原式,
,
故选:D.
8.C
解:
A、∵是无理数,故是无理数
B、∵是无理数,故是无理数
C、为有理数
D、∵是无理数,故是无理数
故选:C
9.A
解:设直角三角形的两条直角边分别为a、b,斜边为c.
根据题意,得,.
∵,
∴.
∴.
∵c>0,
∴.
故选:A
10.B
解:,
所以是型无理数,
故选:B.
11.7
解:∵的小数部分为a,4<<5,
∴a=-4,
∴.
故答案为7
12.5
解:=5.
故答案为:5.
13..
解:根据题意得>0,
∴b>0,
∴原式=
=.
故答案为.
14.2
解:原式=,
故答案为:2.
15.2
解:∵,
∴,
∴,
∴n=2.
故填:2.
16.(1),;(2)x=0.236;(3)a=2.36.
解:(1),
;
(2)∵,
故x=0.236;
(3)由
可得,
即,
故a=2.36.
17.(1)a=5,b=﹣1;(2)b2+2a=14﹣2.
解:(1)∵1<<2,
∴5<4+<6,
∴a=5,b=﹣1;
(2)∵a=5,b=﹣1,
∴b2+2a=(-1)2+2×5=4﹣2+10=14﹣2.
18.
解:∵两个正方形木板的面积分别为18dm2和32dm2,
∴这两个正方形的边长分别为:=3(dm),=4(dm),
∴剩余木料的面积为:(4﹣3)×3=×3=6(dm2).
19.(1);(2)能,见解析
解:(1)设斜边上的高为h,
根据勾股定理:AB2=AC2+BC2;
∴,;
∴.
解得;
(2)能,作图如下:
20.(1)5千米;(2)(+2)平方千米.
解:(1)如图,连接AC,∵∠B=90,AB=BC=5千米,
∴AC===5(千米);
(2)∵AC2=(5)2=50,CD2+AD2=()2+(4)2=50,
∴AC2=CD2+AD2,
则∠D=90,
S四边形ABCD=S△ABC+S△ACD
=×5×5+××4
=(+2)平方千米.
