人教版八上高分笔记之导与练 11.2.2 三角形的外角(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 11.2.2 三角形的外角(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 19:46:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.2.2三角形的外角
知识要点:
1.三角形的一边与另一边的??
??组成的角叫做三角形的外角.
2.三角形的外角等于与它__
_____的两个内角的和.
3.如图,∠1是ΔABC的一个
,∠2=
+
__
∠1+∠2+∠3=?
?度.?
易错点睛
判断题:三角形的外角一定大于三角形的内角.(
??)?
典型例题
题型一
三角尺的组合问题
将一副直角三角尺按如图所示的方式放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上,则∠α的度数是(??????)
A.45°
B.60°
C.75°
D.85°
变式练习:
如图,将分别含有30°,450角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠a的度数为___
?
将一副直角三角尺按如图所示的方式摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,∠B=45°,∠E=30°,∠BCE=40°,则∠CDF的度数为___
°?
题型二
内外角性质的综合应用
如图,在ΔABC中,AD,BE分别是∠BAC,∠ABC的平分线.求证:∠BED=90°-∠C.?
变式练习:
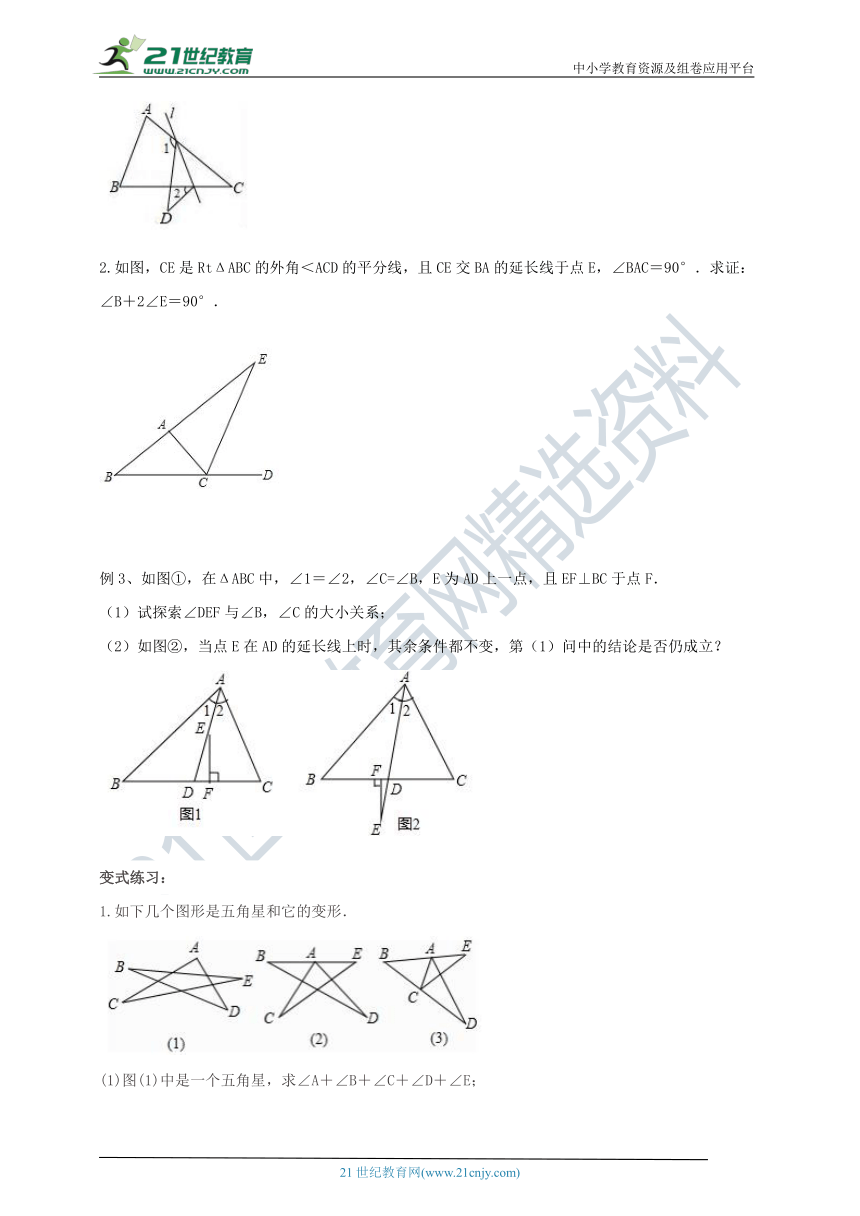
如图,在ΔABC中,∠C=36.若将ΔABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是(?)
A.36°
B.72°
C.50°
D.46°
2.如图,CE是RtΔABC的外角<ACD的平分线,且CE交BA的延长线于点E,∠BAC=90°.求证:∠B+2∠E=90°.
例3、如图①,在ΔABC中,∠1=∠2,∠C=∠B,E为AD上一点,且EF⊥BC于点F.
(1)试探索∠DEF与∠B,∠C的大小关系;
(2)如图②,当点E在AD的延长线上时,其余条件都不变,第(1)问中的结论是否仍成立?
变式练习:
1.如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E;
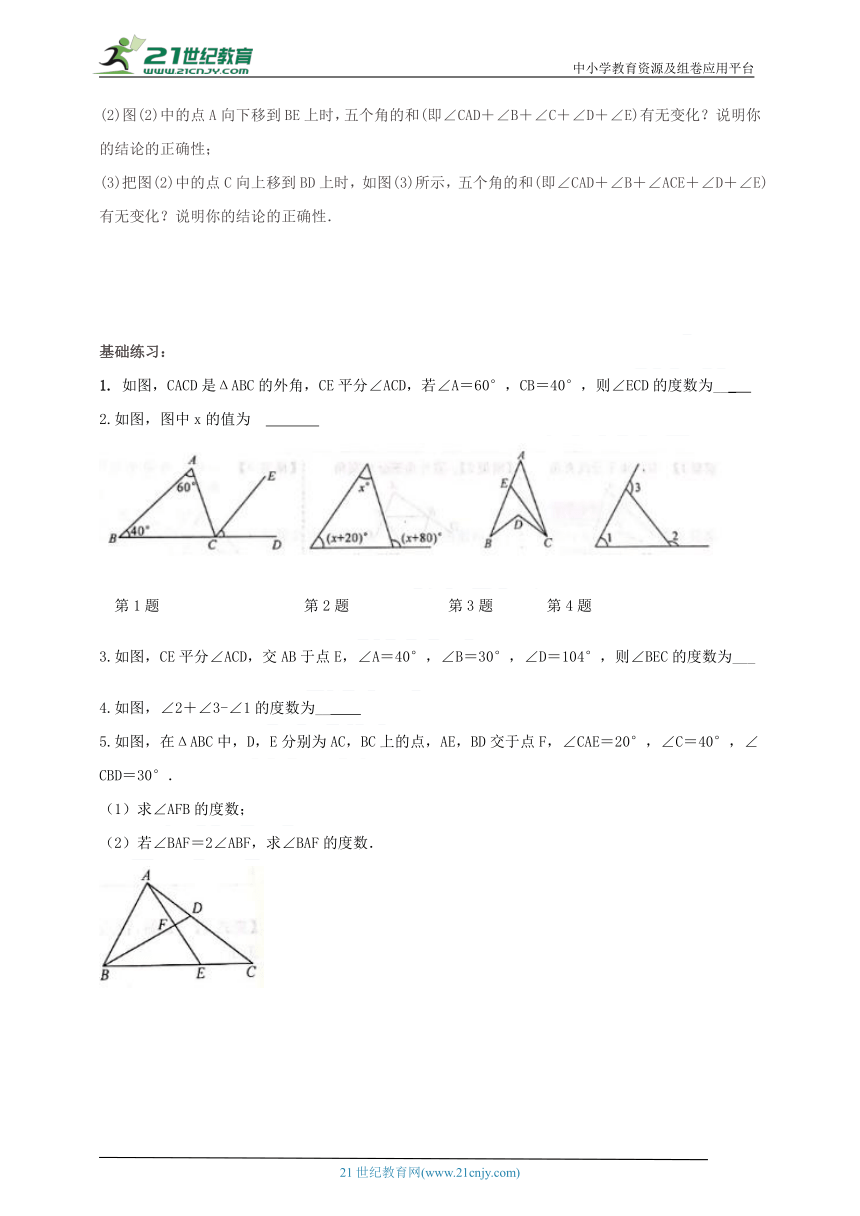
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你的结论的正确性;
(3)把图(2)中的点C向上移到BD上时,如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化?说明你的结论的正确性.
基础练习:
如图,CACD是ΔABC的外角,CE平分∠ACD,若∠A=60°,CB=40°,则∠ECD的度数为___
2.如图,图中x的值为???
第1题
第2题
第3题
第4题
3.如图,CE平分∠ACD,交AB于点E,∠A=40°,∠B=30°,∠D=104°,则∠BEC的度数为___
4.如图,∠2+∠3-∠1的度数为__
5.如图,在ΔABC中,D,E分别为AC,BC上的点,AE,BD交于点F,∠CAE=20°,∠C=40°,∠CBD=30°.
(1)求∠AFB的度数;
(2)若∠BAF=2∠ABF,求∠BAF的度数.
6.如图,在ΔABC中,∠B=∠C,AE平分ΔABC的外角∠CAD.求证:AE//BC.
综合题探究
7.(1)【问题背景】如图1,在ΔABC中,∠ACB的平分线与ΔABC的外角∠ABF的平分线交于点E.
①【特例探寻】若/ABC=80°,CACB=60°,直接写出的值为_______
②【一般结论】求的值;
(2)【变式迁移】如图2,AB//CD,F为CD上一点,CABE的平分线与∠EFC的平分线交于点P,试探究∠P与∠E的数量关系,说明理由.
答案:
知识要点:
1.三角形的一边与另一边的??延长线??组成的角叫做三角形的外角.
2.三角形的外角等于与它__不相邻_____的两个内角的和.
3.如图,∠1是ΔABC的一个外角,∠2=∠BAC+∠BCA
∠1+∠2+∠3=?360?度.?
易错点睛
判断题:三角形的外角一定大于三角形的内角.(
x??)?
解析:①若外角为锐角,则外角小于相邻的内角;②若外角为直角,则外角等于相邻的内角。
典型例题
题型一
三角尺的组合问题
将一副直角三角尺按如图所示的方式放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上,则∠α的度数是(??????)
A.45°
B.60°
C.75°
D.85°
答案:C
解析:三角尺组合求角度,首先明确一副三角尺各角的度数,然后利用三角形内角和定理及其推论,并结合相关角之间的关系求解。
变式练习:
如图,将分别含有30°,450角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠a的度数为___140°?
将一副直角三角尺按如图所示的方式摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,∠B=45°,∠E=30°,∠BCE=40°,则∠CDF的度数为___25°?
题型二
内外角性质的综合应用
如图,在ΔABC中,AD,BE分别是∠BAC,∠ABC的平分线.求证:∠BED=90°-∠C.?
证明::AD,BE分别是∠BAC,∠ABC的平分线,
∠BAE=∠BAC,∠ABE=∠ABC,?
∠BED=∠BAB+∠ABB=(∠BAC+∠ABC)=(180°-∠C)=90°-∠C.
变式练习:
如图,在ΔABC中,∠C=36.若将ΔABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是(?B?)
A.36°
B.72°
C.50°
D.46°
2.如图,CE是RtΔABC的外角<ACD的平分线,且CE交BA的延长线于点E,∠BAC=90°.求证:∠B+2∠E=90°.
证明:CE是∠ACD的平分线,
∴∠ACE=∠DCE.?
∴∠LBAC=∠ACE+∠E=90°,?
∠DCE=∠B+∠E,?
∠ACE=90°-∠E=∠B+∠E.?
∴∠B+2∠E=90°.?
例3、如图①,在ΔABC中,∠1=∠2,∠C=∠B,E为AD上一点,且EF⊥BC于点F.
(1)试探索∠DEF与∠B,∠C的大小关系;
(2)如图②,当点E在AD的延长线上时,其余条件都不变,第(1)问中的结论是否仍成立?
分析:(1)过点A作AG⊥BC于点G,则EF∥AG,故∠DEF=∠DAG,根据直角三角形的性质可知∠CAG=90°-∠C,再由三角形内角和定理可知∠BAC=180°-∠B-∠C,根据∠1=∠2可知,∠2=∠BAC=(180°-∠B-∠C),再根据∠DAG=∠2-∠CAG即可得出结论;
(2)过点A作AH⊥BC于H,根据直角三角形两锐角互余表示出∠CAH,根据角平分线的定义可得∠2,再表示出∠DAH,然后根据三角形的内角和定理可得∠DEF=∠DAH.
解答:(1)解:如图1所示,过点A作AG⊥BC于点G,则EF∥AG,∠DEF=∠DAG,
∵∠AGC=90°,
∴∠CAG=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C,
∵∠1=∠2,
∴∠2=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C).
∵∠DAG=∠2-∠CAG=90°-(∠B+∠C)-(90°-∠C)=(∠C-∠B),
即∠DEF=(∠C-∠B);
变式练习:
1.如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E;
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你的结论的正确性;
(3)把图(2)中的点C向上移到BD上时,如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化?说明你的结论的正确性.
解:(1)如图,连接CD
在△ACD中,根据三角形内角和定理,得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°.
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.
∵∠BAC=∠C+∠E,∠EAD=∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°;
(3)无变化.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
基础练习:
如图,CACD是ΔABC的外角,CE平分∠ACD,若∠A=60°,CB=40°,则∠ECD的度数为___50°
2.如图,图中x的值为???60
第1题
第2题
第3题
第4题
3.如图,CE平分∠ACD,交AB于点E,∠A=40°,∠B=30°,∠D=104°,则∠BEC的度数为?57°
4.如图,∠2+∠3-∠1的度数为___180°
5.如图,在ΔABC中,D,E分别为AC,BC上的点,AE,BD交于点F,∠CAE=20°,∠C=40°,∠CBD=30°.
(1)求∠AFB的度数;
(2)若∠BAF=2∠ABF,求∠BAF的度数.
答案:(1)900(2)600
6.如图,在ΔABC中,∠B=∠C,AE平分ΔABC的外角∠CAD.求证:AE//BC.
解:∵∠B=∠C,∴∠CAD=∠B+∠C=2∠C,∵AE平分∠CAD,
∴4∠EAC=∠CAD=∠C,?
∴AE//BC.?
综合题探究
7.(1)【问题背景】如图1,在ΔABC中,∠ACB的平分线与ΔABC的外角∠ABF的平分线交于点E.
①【特例探寻】若/ABC=80°,CACB=60°,直接写出的值为_______
②【一般结论】求的值;
(2)【变式迁移】如图2,AB//CD,F为CD上一点,CABE的平分线与∠EFC的平分线交于点P,试探究∠P与∠E的数量关系,说明理由.
解:(1)
(2)设∠ABF=2y,∠ACF=2x,在ΔABC中,∠ABF=∠A+ACB,
∠A=∠ABF-∠ACB=2y-2x=2(y-x).?
∵CE平分∠ACB,BE平分∠AFB,
4∠ECF=∠ACF=x,∠EBF=∠ABF=y.?
在ΔEBC中,∠E=∠EBF-∠ECF=y-x,==
∠E=2∠P,理由如下:设∠EBA=2x,∠EFC=2y,设EF,PF与AB分别交于点N,M
∵BP平分∠EBA,FP平分∠EFC,
∴∠PBA=∠EBA=x,∠PFC=∠EFC=y.AB//CD,∴∠ENA=∠EFC=2y,
∠PMA=∠PFC=y.∠E=∠ENA-∠EBA=2y-2x=2(y-x),
∠P=∠PMA-∠PBA=y-x,∴∠E=2∠P.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.2.2三角形的外角
知识要点:
1.三角形的一边与另一边的??
??组成的角叫做三角形的外角.
2.三角形的外角等于与它__
_____的两个内角的和.
3.如图,∠1是ΔABC的一个
,∠2=
+
__
∠1+∠2+∠3=?
?度.?
易错点睛
判断题:三角形的外角一定大于三角形的内角.(
??)?
典型例题
题型一
三角尺的组合问题
将一副直角三角尺按如图所示的方式放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上,则∠α的度数是(??????)
A.45°
B.60°
C.75°
D.85°
变式练习:
如图,将分别含有30°,450角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠a的度数为___
?
将一副直角三角尺按如图所示的方式摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,∠B=45°,∠E=30°,∠BCE=40°,则∠CDF的度数为___
°?
题型二
内外角性质的综合应用
如图,在ΔABC中,AD,BE分别是∠BAC,∠ABC的平分线.求证:∠BED=90°-∠C.?
变式练习:
如图,在ΔABC中,∠C=36.若将ΔABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是(?)
A.36°
B.72°
C.50°
D.46°
2.如图,CE是RtΔABC的外角<ACD的平分线,且CE交BA的延长线于点E,∠BAC=90°.求证:∠B+2∠E=90°.
例3、如图①,在ΔABC中,∠1=∠2,∠C=∠B,E为AD上一点,且EF⊥BC于点F.
(1)试探索∠DEF与∠B,∠C的大小关系;
(2)如图②,当点E在AD的延长线上时,其余条件都不变,第(1)问中的结论是否仍成立?
变式练习:
1.如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E;
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你的结论的正确性;
(3)把图(2)中的点C向上移到BD上时,如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化?说明你的结论的正确性.
基础练习:
如图,CACD是ΔABC的外角,CE平分∠ACD,若∠A=60°,CB=40°,则∠ECD的度数为___
2.如图,图中x的值为???
第1题
第2题
第3题
第4题
3.如图,CE平分∠ACD,交AB于点E,∠A=40°,∠B=30°,∠D=104°,则∠BEC的度数为___
4.如图,∠2+∠3-∠1的度数为__
5.如图,在ΔABC中,D,E分别为AC,BC上的点,AE,BD交于点F,∠CAE=20°,∠C=40°,∠CBD=30°.
(1)求∠AFB的度数;
(2)若∠BAF=2∠ABF,求∠BAF的度数.
6.如图,在ΔABC中,∠B=∠C,AE平分ΔABC的外角∠CAD.求证:AE//BC.
综合题探究
7.(1)【问题背景】如图1,在ΔABC中,∠ACB的平分线与ΔABC的外角∠ABF的平分线交于点E.
①【特例探寻】若/ABC=80°,CACB=60°,直接写出的值为_______
②【一般结论】求的值;
(2)【变式迁移】如图2,AB//CD,F为CD上一点,CABE的平分线与∠EFC的平分线交于点P,试探究∠P与∠E的数量关系,说明理由.
答案:
知识要点:
1.三角形的一边与另一边的??延长线??组成的角叫做三角形的外角.
2.三角形的外角等于与它__不相邻_____的两个内角的和.
3.如图,∠1是ΔABC的一个外角,∠2=∠BAC+∠BCA
∠1+∠2+∠3=?360?度.?
易错点睛
判断题:三角形的外角一定大于三角形的内角.(
x??)?
解析:①若外角为锐角,则外角小于相邻的内角;②若外角为直角,则外角等于相邻的内角。
典型例题
题型一
三角尺的组合问题
将一副直角三角尺按如图所示的方式放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上,则∠α的度数是(??????)
A.45°
B.60°
C.75°
D.85°
答案:C
解析:三角尺组合求角度,首先明确一副三角尺各角的度数,然后利用三角形内角和定理及其推论,并结合相关角之间的关系求解。
变式练习:
如图,将分别含有30°,450角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠a的度数为___140°?
将一副直角三角尺按如图所示的方式摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,∠B=45°,∠E=30°,∠BCE=40°,则∠CDF的度数为___25°?
题型二
内外角性质的综合应用
如图,在ΔABC中,AD,BE分别是∠BAC,∠ABC的平分线.求证:∠BED=90°-∠C.?
证明::AD,BE分别是∠BAC,∠ABC的平分线,
∠BAE=∠BAC,∠ABE=∠ABC,?
∠BED=∠BAB+∠ABB=(∠BAC+∠ABC)=(180°-∠C)=90°-∠C.
变式练习:
如图,在ΔABC中,∠C=36.若将ΔABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是(?B?)
A.36°
B.72°
C.50°
D.46°
2.如图,CE是RtΔABC的外角<ACD的平分线,且CE交BA的延长线于点E,∠BAC=90°.求证:∠B+2∠E=90°.
证明:CE是∠ACD的平分线,
∴∠ACE=∠DCE.?
∴∠LBAC=∠ACE+∠E=90°,?
∠DCE=∠B+∠E,?
∠ACE=90°-∠E=∠B+∠E.?
∴∠B+2∠E=90°.?
例3、如图①,在ΔABC中,∠1=∠2,∠C=∠B,E为AD上一点,且EF⊥BC于点F.
(1)试探索∠DEF与∠B,∠C的大小关系;
(2)如图②,当点E在AD的延长线上时,其余条件都不变,第(1)问中的结论是否仍成立?
分析:(1)过点A作AG⊥BC于点G,则EF∥AG,故∠DEF=∠DAG,根据直角三角形的性质可知∠CAG=90°-∠C,再由三角形内角和定理可知∠BAC=180°-∠B-∠C,根据∠1=∠2可知,∠2=∠BAC=(180°-∠B-∠C),再根据∠DAG=∠2-∠CAG即可得出结论;
(2)过点A作AH⊥BC于H,根据直角三角形两锐角互余表示出∠CAH,根据角平分线的定义可得∠2,再表示出∠DAH,然后根据三角形的内角和定理可得∠DEF=∠DAH.
解答:(1)解:如图1所示,过点A作AG⊥BC于点G,则EF∥AG,∠DEF=∠DAG,
∵∠AGC=90°,
∴∠CAG=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C,
∵∠1=∠2,
∴∠2=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C).
∵∠DAG=∠2-∠CAG=90°-(∠B+∠C)-(90°-∠C)=(∠C-∠B),
即∠DEF=(∠C-∠B);
变式练习:
1.如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E;
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你的结论的正确性;
(3)把图(2)中的点C向上移到BD上时,如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化?说明你的结论的正确性.
解:(1)如图,连接CD
在△ACD中,根据三角形内角和定理,得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°.
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.
∵∠BAC=∠C+∠E,∠EAD=∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°;
(3)无变化.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
基础练习:
如图,CACD是ΔABC的外角,CE平分∠ACD,若∠A=60°,CB=40°,则∠ECD的度数为___50°
2.如图,图中x的值为???60
第1题
第2题
第3题
第4题
3.如图,CE平分∠ACD,交AB于点E,∠A=40°,∠B=30°,∠D=104°,则∠BEC的度数为?57°
4.如图,∠2+∠3-∠1的度数为___180°
5.如图,在ΔABC中,D,E分别为AC,BC上的点,AE,BD交于点F,∠CAE=20°,∠C=40°,∠CBD=30°.
(1)求∠AFB的度数;
(2)若∠BAF=2∠ABF,求∠BAF的度数.
答案:(1)900(2)600
6.如图,在ΔABC中,∠B=∠C,AE平分ΔABC的外角∠CAD.求证:AE//BC.
解:∵∠B=∠C,∴∠CAD=∠B+∠C=2∠C,∵AE平分∠CAD,
∴4∠EAC=∠CAD=∠C,?
∴AE//BC.?
综合题探究
7.(1)【问题背景】如图1,在ΔABC中,∠ACB的平分线与ΔABC的外角∠ABF的平分线交于点E.
①【特例探寻】若/ABC=80°,CACB=60°,直接写出的值为_______
②【一般结论】求的值;
(2)【变式迁移】如图2,AB//CD,F为CD上一点,CABE的平分线与∠EFC的平分线交于点P,试探究∠P与∠E的数量关系,说明理由.
解:(1)
(2)设∠ABF=2y,∠ACF=2x,在ΔABC中,∠ABF=∠A+ACB,
∠A=∠ABF-∠ACB=2y-2x=2(y-x).?
∵CE平分∠ACB,BE平分∠AFB,
4∠ECF=∠ACF=x,∠EBF=∠ABF=y.?
在ΔEBC中,∠E=∠EBF-∠ECF=y-x,==
∠E=2∠P,理由如下:设∠EBA=2x,∠EFC=2y,设EF,PF与AB分别交于点N,M
∵BP平分∠EBA,FP平分∠EFC,
∴∠PBA=∠EBA=x,∠PFC=∠EFC=y.AB//CD,∴∠ENA=∠EFC=2y,
∠PMA=∠PFC=y.∠E=∠ENA-∠EBA=2y-2x=2(y-x),
∠P=∠PMA-∠PBA=y-x,∴∠E=2∠P.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
