人教版八上高分笔记之导与练 11.3 多边形及其内角和(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 11.3 多边形及其内角和(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.3多边形及其内角和
知识要点
1.在平面内,由一些线段
组成的封闭图形叫多边形。
2.连接多边形
的两个顶点的线段,叫做多边形的对角线.
3.各条边都
,各个角都
的多边形叫正多边形.
4.n边形的内角和为
?,外角和为
5.正n边形的每一个内角的度数为
_________?,每一个外角的度数为________
易错点睛
1.八边形对角线的总条数为??______
2.若n边形的内角和等于外角和的3倍,则n的值为?_________
典型例题
题型一
求不规则图形中相关角的和
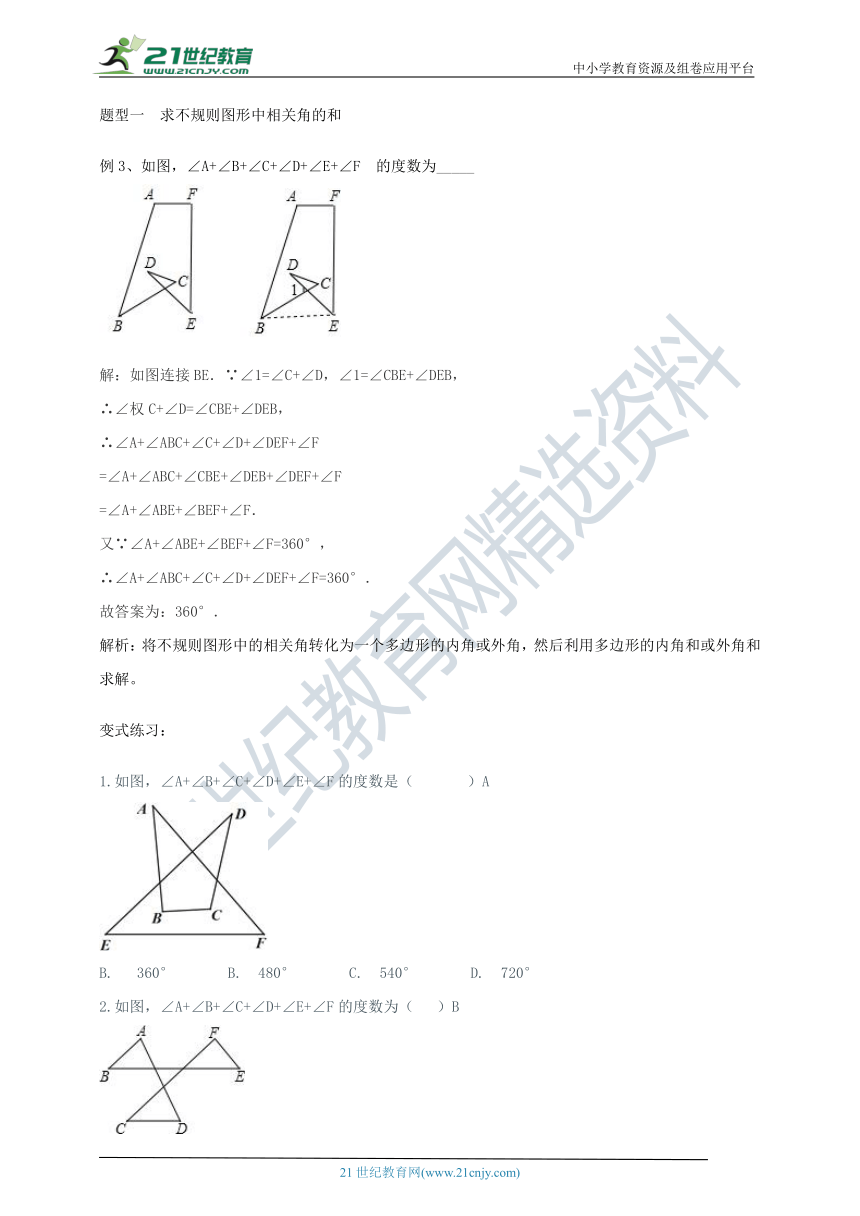
如图,∠A+∠B+∠C+∠D+∠E+∠F?的度数为_____
变式练习:
1.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是(???
)
?360°???
B.?480°???
C.?540°???
D.?720°
2.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为(
)
A.180°
B.360°
C.540°
D.720°
题型二
多边形截角问题
一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原多边形的边数是(????)
A.10
B.11
C.12
D.10或11或12
变式练习:
如图为长方形ABCD,一条直线将该长方形分割成个多边形,若这两个多边形的内角和分别为a°和b°,则a+b不可能是(??
?)
A.360
B.540
C.630
D.720
一张多边形纸片按如图所示的剪法剪去一个内角后,得到一个内角和是外角和4倍的新多边形,则原多边形的边数为(???)?
A.8
B.9
C.10
D.11
基础练习:
一个多边形的内角和与外角和的和为1800°,这个多边形的边数是(
)
A.8
B.9??C.10????D.11?
2.如图,小明从点A出发沿直线前进10m到达点B,向左转45°后又沿直线前进10m到达点C,再向左转45°后沿直线前进10米到达点D,·,照这样走下去,小明第一次回到出发点A时所走的路程为(
)
A.100m
B.80m
C.60m
D.40m
第2题
第3题
第5题
如图,将四边形纸片ABCD沿MN折叠,若<1+<2=130°,则<B+<C的度数为(
)
A.115°
B.130°
C.135°
D.150°?
4.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是(??
)
A.8???????B.9?
C.10
D.11
5.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的度数为___
6.一张多边形纸片的边数为n.
(1)当n=11时,求这个多边形对角线的总条数
(2)若将这个多边形纸片沿一条直线剪下一个三角形后变成一个八边形,则n的值是
7.如图,已知六边形ABCDEF的每个内角都相等.
(1)求∠A的度数;(2)求证:AB//DE.
综合题探究
8.(1)如图1,2,试探究∠1,∠2与∠3,∠4之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决下面的问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,MDA的平分线,∠B+∠C=240°,求∠E的度数.
答案:
知识要点
1.在平面内,由一些线段首尾顺次相接组成的封闭图形叫多边形。
2.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3.各条边都相等,各个角都相等的多边形叫正多边形.
4.n边形的内角和为(n-2)·180°?,外角和为360°
5.正n边形的每一个内角的度数为?,每一个外角的度数为
易错点睛
1.八边形对角线的总条数为??20
【点睛)易误认为n边形对角线为n(n-3)条,而应是?条。
2.若n边形的内角和等于外角和的3倍,则n的值为?8
【点晴】熟记多边形内角和与外角和公式
典型例题
题型一
求不规则图形中相关角的和
如图,∠A+∠B+∠C+∠D+∠E+∠F?的度数为_____
解:如图连接BE.∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠权C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
又∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
故答案为:360°.
解析:将不规则图形中的相关角转化为一个多边形的内角或外角,然后利用多边形的内角和或外角和求解。
变式练习:
1.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是(???
)A
?360°???
B.?480°???
C.?540°???
D.?720°
2.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为(
)B
A.180°
B.360°
C.540°
D.720°
题型二
多边形截角问题
一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,
则原多边形的边数是(??????)
A.10
B.11
C.12
D.10或11或12
答案:D
技巧点拨
多边形(边数大于3)截去一个角有三种截法:
(1)过不相邻的两顶点截,则新多边形的边数比原多边形的边数少1,如图①;
(2)过一顶点和另一边上的一点截,则新多边形的边数与原多边形的边数相同,如图②;
(3)过相邻两边上的两个非顶点截,则新多边形的边数比原多边形的边数多1,如图③.
变式练习:
如图为长方形ABCD,一条直线将该长方形分割成个多边形,若这两
个多边形的内角和分别为a°和b°,则a+b不可能是(??C?)
A.360
B.540
C.630
D.720
一张多边形纸片按如图所示的剪法剪去一个内角后,得到一个内角和是外
角和4倍的新多边形,则原多边形的边数为(?B??)?
A.8
B.9
C.10
D.11
【解析】设原多边形的边数为x,则(x+1-2)x
180=4x360,解得x=9.
基础练习:
一个多边形的内角和与外角和的和为1800°,这个多边形的边数是(
C
)
A.8
B.9??C.10????D.11?
2.如图,小明从点A出发沿直线前进10m到达点B,向左转45°后又沿直线前进10m到达点C,再向左转45°后沿直线前进10米到达点D,·,照这样走下去,小明第一次回到出发点A时所走的路程为(
B
)
A.100m
B.80m
C.60m
D.40m
第2题
第3题
第5题
3.如图,将四边形纸片ABCD沿MN折叠,若<1+<2=130°,则<B+<C的度数为(
A
)
A.115°
B.130°
C.135°
D.150°?
4.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是(??D
)
A.8???????B.9?
C.10
D.11
5.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的度数为___80°
6.一张多边形纸片的边数为n.
(1)当n=11时,求这个多边形对角线的总条数;1
(2)若将这个多边形纸片沿一条直线剪下一个三角形后变成一个八边形,则n的值是7或8或9
解:(1)当n=11时,对角线总条数为?x11(11-3)=44(条):
(2)7或8或9.
7.如图,已知六边形ABCDEF的每个内角都相等.
(1)求∠A的度数;
(2)求证:AB//DE.
解:(1)1200
证明:方法一:连接BE,∠A=∠F=120°,∠A+∠F+∠FEB+∠ABE=360°,
∴∠ABE+∠FEB=120°,又∵∠FED=∠FEB+∠BED=120°,∴∠ABE=∠BED,∴AB//DE;
方法二:延长DC,AB交于点G,可得∠G=60°,∴∠D+∠G=180°,∴AB//DE.
综合题探究
8.(1)如图1,2,试探究∠1,∠2与∠3,∠4之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决下面的问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,MDA的平分线,∠B+∠C=240°,求∠E的度数.
解:(1)设∠1的邻补角为∠5,∠2的邻补角为∠6.∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360∴∠3+∠4=360°-(∠5+∠6).∴∠1+∠5=180°,?
∠2+∠6=180°,∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4;?
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和.
(3)∠B+∠C=240°,由(2)知∠MDA+∠NAD=240.AE,DE分别是∠NAD,
∠MDA的平分线,∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°.∴∠E=180°-(∠ADE+∠DAE)=60°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.3多边形及其内角和
知识要点
1.在平面内,由一些线段
组成的封闭图形叫多边形。
2.连接多边形
的两个顶点的线段,叫做多边形的对角线.
3.各条边都
,各个角都
的多边形叫正多边形.
4.n边形的内角和为
?,外角和为
5.正n边形的每一个内角的度数为
_________?,每一个外角的度数为________
易错点睛
1.八边形对角线的总条数为??______
2.若n边形的内角和等于外角和的3倍,则n的值为?_________
典型例题
题型一
求不规则图形中相关角的和
如图,∠A+∠B+∠C+∠D+∠E+∠F?的度数为_____
变式练习:
1.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是(???
)
?360°???
B.?480°???
C.?540°???
D.?720°
2.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为(
)
A.180°
B.360°
C.540°
D.720°
题型二
多边形截角问题
一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原多边形的边数是(????)
A.10
B.11
C.12
D.10或11或12
变式练习:
如图为长方形ABCD,一条直线将该长方形分割成个多边形,若这两个多边形的内角和分别为a°和b°,则a+b不可能是(??
?)
A.360
B.540
C.630
D.720
一张多边形纸片按如图所示的剪法剪去一个内角后,得到一个内角和是外角和4倍的新多边形,则原多边形的边数为(???)?
A.8
B.9
C.10
D.11
基础练习:
一个多边形的内角和与外角和的和为1800°,这个多边形的边数是(
)
A.8
B.9??C.10????D.11?
2.如图,小明从点A出发沿直线前进10m到达点B,向左转45°后又沿直线前进10m到达点C,再向左转45°后沿直线前进10米到达点D,·,照这样走下去,小明第一次回到出发点A时所走的路程为(
)
A.100m
B.80m
C.60m
D.40m
第2题
第3题
第5题
如图,将四边形纸片ABCD沿MN折叠,若<1+<2=130°,则<B+<C的度数为(
)
A.115°
B.130°
C.135°
D.150°?
4.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是(??
)
A.8???????B.9?
C.10
D.11
5.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的度数为___
6.一张多边形纸片的边数为n.
(1)当n=11时,求这个多边形对角线的总条数
(2)若将这个多边形纸片沿一条直线剪下一个三角形后变成一个八边形,则n的值是
7.如图,已知六边形ABCDEF的每个内角都相等.
(1)求∠A的度数;(2)求证:AB//DE.
综合题探究
8.(1)如图1,2,试探究∠1,∠2与∠3,∠4之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决下面的问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,MDA的平分线,∠B+∠C=240°,求∠E的度数.
答案:
知识要点
1.在平面内,由一些线段首尾顺次相接组成的封闭图形叫多边形。
2.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3.各条边都相等,各个角都相等的多边形叫正多边形.
4.n边形的内角和为(n-2)·180°?,外角和为360°
5.正n边形的每一个内角的度数为?,每一个外角的度数为
易错点睛
1.八边形对角线的总条数为??20
【点睛)易误认为n边形对角线为n(n-3)条,而应是?条。
2.若n边形的内角和等于外角和的3倍,则n的值为?8
【点晴】熟记多边形内角和与外角和公式
典型例题
题型一
求不规则图形中相关角的和
如图,∠A+∠B+∠C+∠D+∠E+∠F?的度数为_____
解:如图连接BE.∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠权C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
又∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
故答案为:360°.
解析:将不规则图形中的相关角转化为一个多边形的内角或外角,然后利用多边形的内角和或外角和求解。
变式练习:
1.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是(???
)A
?360°???
B.?480°???
C.?540°???
D.?720°
2.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为(
)B
A.180°
B.360°
C.540°
D.720°
题型二
多边形截角问题
一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,
则原多边形的边数是(??????)
A.10
B.11
C.12
D.10或11或12
答案:D
技巧点拨
多边形(边数大于3)截去一个角有三种截法:
(1)过不相邻的两顶点截,则新多边形的边数比原多边形的边数少1,如图①;
(2)过一顶点和另一边上的一点截,则新多边形的边数与原多边形的边数相同,如图②;
(3)过相邻两边上的两个非顶点截,则新多边形的边数比原多边形的边数多1,如图③.
变式练习:
如图为长方形ABCD,一条直线将该长方形分割成个多边形,若这两
个多边形的内角和分别为a°和b°,则a+b不可能是(??C?)
A.360
B.540
C.630
D.720
一张多边形纸片按如图所示的剪法剪去一个内角后,得到一个内角和是外
角和4倍的新多边形,则原多边形的边数为(?B??)?
A.8
B.9
C.10
D.11
【解析】设原多边形的边数为x,则(x+1-2)x
180=4x360,解得x=9.
基础练习:
一个多边形的内角和与外角和的和为1800°,这个多边形的边数是(
C
)
A.8
B.9??C.10????D.11?
2.如图,小明从点A出发沿直线前进10m到达点B,向左转45°后又沿直线前进10m到达点C,再向左转45°后沿直线前进10米到达点D,·,照这样走下去,小明第一次回到出发点A时所走的路程为(
B
)
A.100m
B.80m
C.60m
D.40m
第2题
第3题
第5题
3.如图,将四边形纸片ABCD沿MN折叠,若<1+<2=130°,则<B+<C的度数为(
A
)
A.115°
B.130°
C.135°
D.150°?
4.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是(??D
)
A.8???????B.9?
C.10
D.11
5.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的度数为___80°
6.一张多边形纸片的边数为n.
(1)当n=11时,求这个多边形对角线的总条数;1
(2)若将这个多边形纸片沿一条直线剪下一个三角形后变成一个八边形,则n的值是7或8或9
解:(1)当n=11时,对角线总条数为?x11(11-3)=44(条):
(2)7或8或9.
7.如图,已知六边形ABCDEF的每个内角都相等.
(1)求∠A的度数;
(2)求证:AB//DE.
解:(1)1200
证明:方法一:连接BE,∠A=∠F=120°,∠A+∠F+∠FEB+∠ABE=360°,
∴∠ABE+∠FEB=120°,又∵∠FED=∠FEB+∠BED=120°,∴∠ABE=∠BED,∴AB//DE;
方法二:延长DC,AB交于点G,可得∠G=60°,∴∠D+∠G=180°,∴AB//DE.
综合题探究
8.(1)如图1,2,试探究∠1,∠2与∠3,∠4之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决下面的问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,MDA的平分线,∠B+∠C=240°,求∠E的度数.
解:(1)设∠1的邻补角为∠5,∠2的邻补角为∠6.∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360∴∠3+∠4=360°-(∠5+∠6).∴∠1+∠5=180°,?
∠2+∠6=180°,∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4;?
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和.
(3)∠B+∠C=240°,由(2)知∠MDA+∠NAD=240.AE,DE分别是∠NAD,
∠MDA的平分线,∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°.∴∠E=180°-(∠ADE+∠DAE)=60°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
