指数函数及其性质(新课标A)(获奖课件)
文档属性
| 名称 | 指数函数及其性质(新课标A)(获奖课件) | 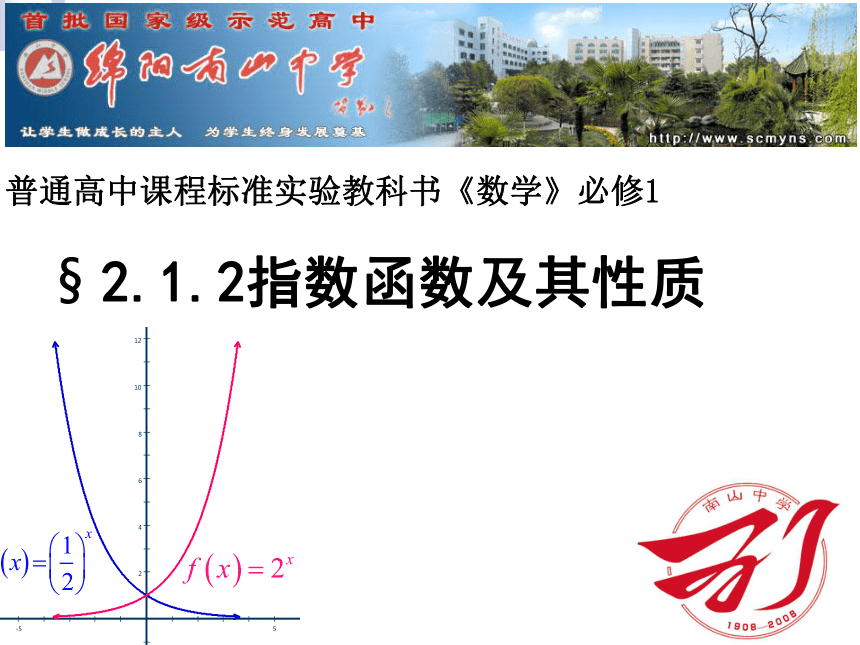 | |
| 格式 | zip | ||
| 文件大小 | 860.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-16 17:14:13 | ||
图片预览







文档简介
(共33张PPT)
普通高中课程标准实验教科书《数学》必修1
§ 2.1.2指数函数及其性质
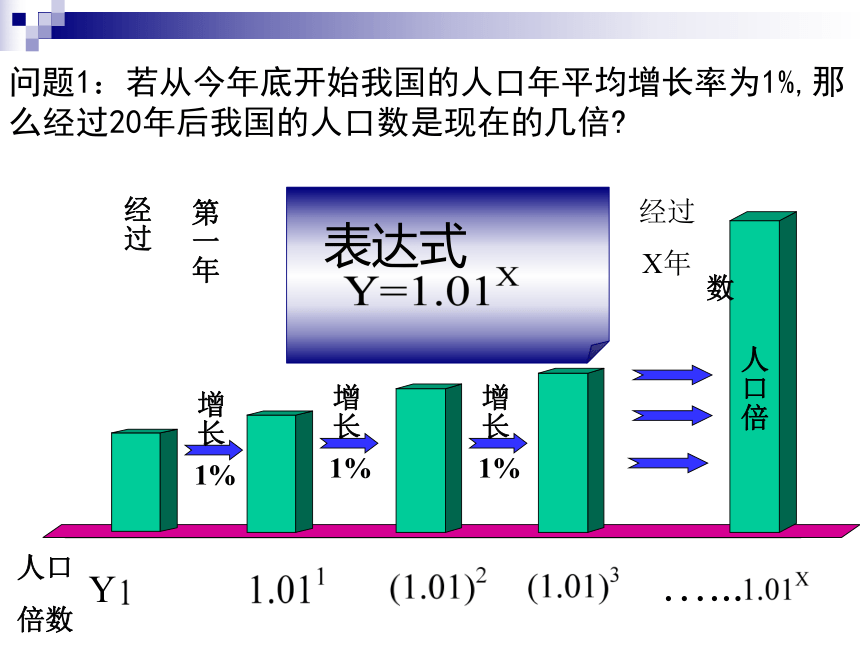
人口问题是全球性问题,由于全球人口迅猛增加,已引起全世界关注 。
我国人口问题更为突出,在耕地面积只占世界7%的国土上,却养育着22%的世界人口.因此,中国的人口问题是公认的社会问题.2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%.
人口倍数
经过
第一年
第二年
第三年
经过
X年
…...
人口
倍数
Y
增长
1%
增长
1%
增长
1%
表达式
问题1:若从今年底开始我国的人口年平均增长率为1%,那么经过20年后我国的人口数是现在的几倍
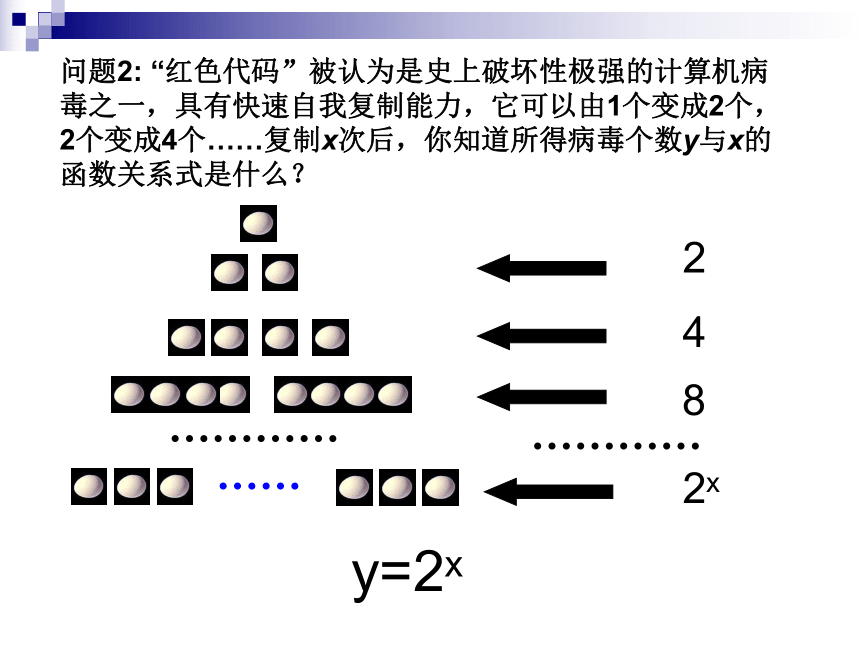
问题2: “红色代码”被认为是史上破坏性极强的计算机病毒之一,具有快速自我复制能力,它可以由1个变成2个,2个变成4个……复制x次后,你知道所得病毒个数y与x的函数关系式是什么?
…………
……
2
4
8
2x
…………
y=2x
指数函数定义:
函数 y=ax (a>0,a≠1)叫做指数函数,
其中x是自变量,函数的定义域为R
想一想
二、探索研究
问题 解析式 共同特征
问题1 Y=1.01X
问题2 Y=2X
指数幂形式
自变量在指数位置
底数是常量
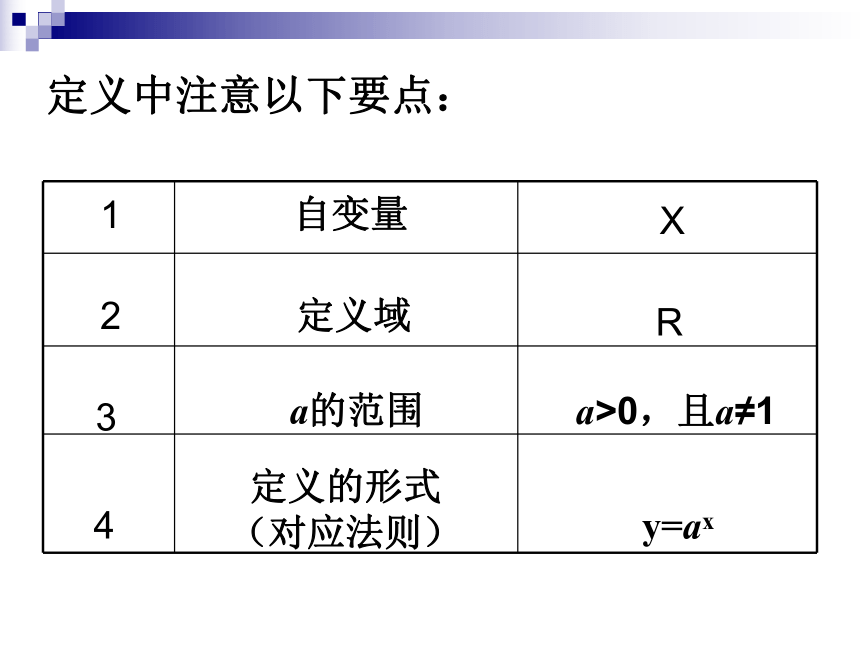
定义中注意以下要点:
1
自变量
X
2
定义域
R
3
a的范围
a>0,且a≠1
4
定义的形式
(对应法则)
y=ax
思考:
为什么要规定
a>0且a≠1呢?
指数函数
了解
(1)
(3)
(2)
探究:函数
是指数函数吗?
不是!指数函数中要求 的系数必须是1
思考:下列函数是指数函数吗,为什么
不是
不是
是
是
y=(-2)x
研究初等函数性质的基本方法和步骤:
1、作出函数图象
2、研究函数性质:
①定义域 ②值域 ③单调性
④奇偶性 ⑤其它
思考:
你能类比前面讨论函数性质时的思路,提出研究指数函数性质的方法吗?
列表 描点 连线
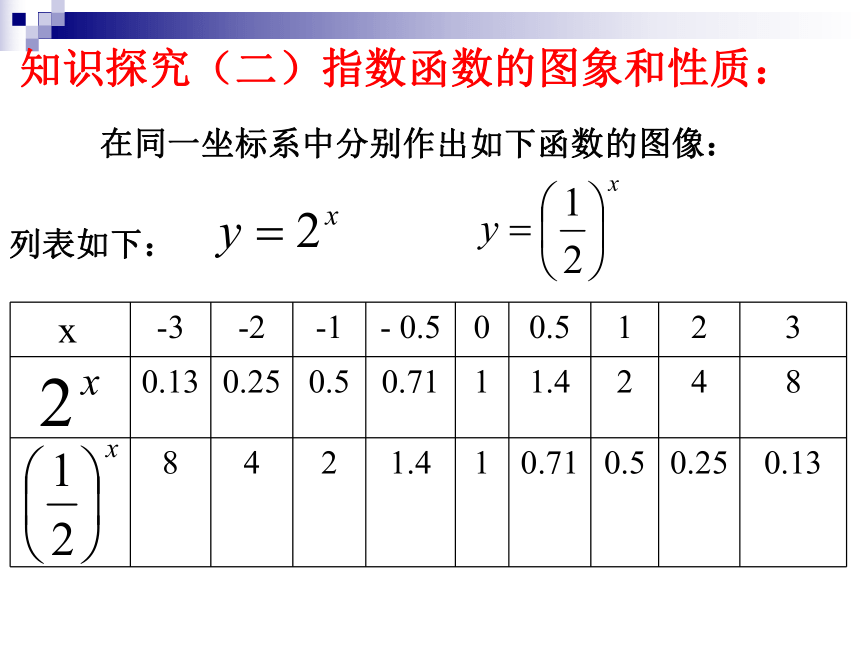
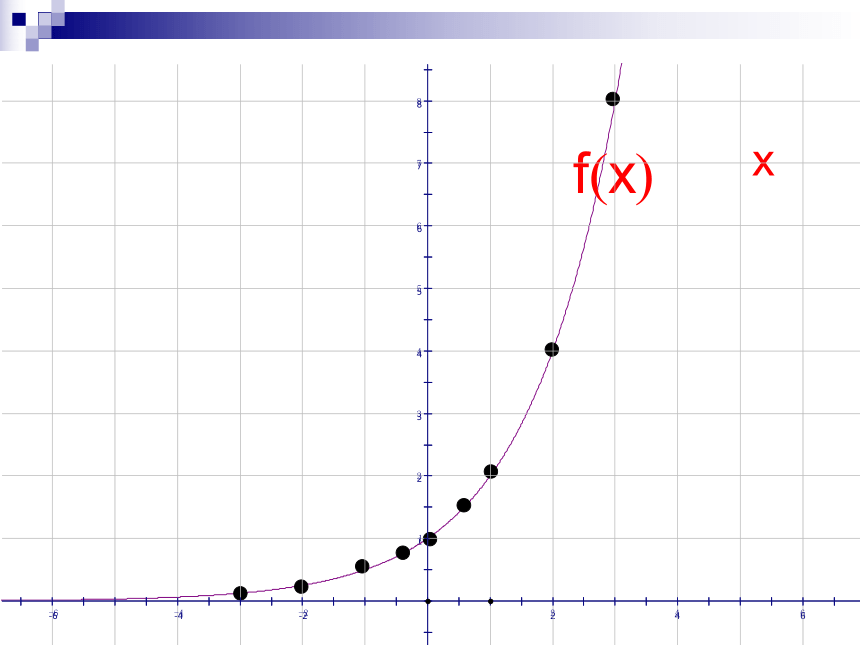
知识探究(二)指数函数的图象和性质:
在同一坐标系中分别作出如下函数的图像:
列表如下:
x -3 -2 -1 - 0.5 0 0.5 1 2 3
0.13 0.25 0.5 0.71 1 1.4 2 4 8
8 4 2 1.4 1 0.71 0.5 0.25 0.13
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
-4
-2
2
4
6
5
4
3
2
1
h
x
(
)
=
3
x
不同底的图像的特征
6
5
4
3
2
1
-4
-2
2
4
q
x
(
)
=( )
1
3
x
不同底的图像的特征
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
普通高中课程标准实验教科书《数学》必修1
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
请同学们结合图像特征思考以下问题:
1、图像分布在哪些象限,与x轴的相对位置关系如何?
2、图象关于原点对称吗?关于y轴对称吗?
3、函数图象过定点吗?
4、自左向右看,图象上升(下降)的趋势是怎样的?
5、在第一象限内的图象纵坐标具有什么特点?
6、在第二象限内的图象纵坐标具有什么特点?
图象特征 函数性质
向x轴正负方向无限延伸
函数的定义域为R
函数图象都在x轴上方
函数的值域为全体正实数
图象关于原点和y轴不对称
非奇非偶函数
函数图象都过定点(0,1)
自左向右看,
图象逐渐上升
在R上是增函数
自左向右看,
图象逐渐下降
在R上是减函数
在第二象限内的图
象纵坐标都小于1
在第一象限内的图
象纵坐标都小于1
在第一象限内的图
象纵坐标都大于1
在第二象限内的图
象纵坐标都大于1
思考:底数的变化会对图像产生什么影响
理论迁移
指数函数
例:已知指数函数
的图像经过点(3,π),求f(0),
f(1),f(-3)
解:因为f(x)=ax的图像经过点(3,π),
所以
f (3)=π,解得a=
,f(x)=
指数函数
理论迁移
例2:比较大小:
(1)
解:因为f(x)=1.7x在R上是增函数,
且2.5 < 3,
所以1.7 2.5< 1.73 。
1.72.5 ,1.73
1.7x
指数函数
理论迁移
例2:比较大小:
(2) 0.8-0.1,0.8-0.2
解:因为f(x)=0.8x在R上是减函数,
且-0.1>-0.2,
所以0.8-0.1 < 0.8-0.2。
0.8x
指数函数
理论迁移
例2:比较大小:
(3)1.7 0.3,0.93.1
解:由指数函数的性质知1.70.3 > 1.70 =1,而
0.93.1 < 0.90 =1
所以
1.70.3 > 0.93.1
y=13×(1+1%)x =13 ×1.01x
当x=20时,y= 13 ×1.0120≈16(亿)
所以经过20年后,我国人口最多为16亿。
截止到1999年底,我国人口约13亿,如果能将人口年平均增长率控制在1%,那么经过20年后我国的人口数最多为多少(精确到亿)?
在实际问题中,经常会遇到类似的指数增长模型:
设原有量为N,每次的增长率为P,经过X次增长,该量增长到Y,则
Y=N(1+P)X
形如y=kax的函数是一种指数型函数,这是非常有用的函数模型。
考古中的指数函数
知识扩展
含C物质的C-14含量在C元素中所含的比例几乎是保持恒定的,如果含C物质一旦停止与大气的交换关系,则该物质的C-14含量不在得到新的补充,而原有的C-14按照衰变规律减少,每隔5730年减少一半,因此只要测出含C物质中C-14的减少的程度,就可以计算出它停止与大气进行交换的年代,这就是C-14测年的原理。
测年方法进入考古学研究被誉为考古学发展史上的一次革命,它将考古学研究中得到的相对年代转变为绝对年代,给考古学带来了质的飞跃,使研究更加科学化,促进了考古学研究的深入。其中测算公式是一个指数式。
安阳曹操墓是真是假?
魏武帝曹操(公元155~220)
1、指数函数的定义;
2、指数函数图象的作法;
3、指数函数的图象和性质.
小 结
函数 叫做指数函数,其中x是自变量.
列表 描点 连线
图
象
性
质
(1)定义域
(2)值域
(3)定点
(5)函数值的分布情况
(4)单调性
x
y
o
1
x
y
o
1
R
( 0 , + ∞)
过定点 ( 0 , 1 ),即x=0时,y=1
当x>0时,y>1
当x<0时,0<y<1
当x>0时, 0<y<1
当x<0时, y>1
在R上是增函数
在R上是减函数
a > 1
0 < a < 1
3.指数函数的图象和性质
作业:
教科书P59,习题2.1A组
5,6,7,8,9
谢谢各位老师和同学们!
再见!
百年南山,百年经典
普通高中课程标准实验教科书《数学》必修1
§ 2.1.2指数函数及其性质
人口问题是全球性问题,由于全球人口迅猛增加,已引起全世界关注 。
我国人口问题更为突出,在耕地面积只占世界7%的国土上,却养育着22%的世界人口.因此,中国的人口问题是公认的社会问题.2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%.
人口倍数
经过
第一年
第二年
第三年
经过
X年
…...
人口
倍数
Y
增长
1%
增长
1%
增长
1%
表达式
问题1:若从今年底开始我国的人口年平均增长率为1%,那么经过20年后我国的人口数是现在的几倍
问题2: “红色代码”被认为是史上破坏性极强的计算机病毒之一,具有快速自我复制能力,它可以由1个变成2个,2个变成4个……复制x次后,你知道所得病毒个数y与x的函数关系式是什么?
…………
……
2
4
8
2x
…………
y=2x
指数函数定义:
函数 y=ax (a>0,a≠1)叫做指数函数,
其中x是自变量,函数的定义域为R
想一想
二、探索研究
问题 解析式 共同特征
问题1 Y=1.01X
问题2 Y=2X
指数幂形式
自变量在指数位置
底数是常量
定义中注意以下要点:
1
自变量
X
2
定义域
R
3
a的范围
a>0,且a≠1
4
定义的形式
(对应法则)
y=ax
思考:
为什么要规定
a>0且a≠1呢?
指数函数
了解
(1)
(3)
(2)
探究:函数
是指数函数吗?
不是!指数函数中要求 的系数必须是1
思考:下列函数是指数函数吗,为什么
不是
不是
是
是
y=(-2)x
研究初等函数性质的基本方法和步骤:
1、作出函数图象
2、研究函数性质:
①定义域 ②值域 ③单调性
④奇偶性 ⑤其它
思考:
你能类比前面讨论函数性质时的思路,提出研究指数函数性质的方法吗?
列表 描点 连线
知识探究(二)指数函数的图象和性质:
在同一坐标系中分别作出如下函数的图像:
列表如下:
x -3 -2 -1 - 0.5 0 0.5 1 2 3
0.13 0.25 0.5 0.71 1 1.4 2 4 8
8 4 2 1.4 1 0.71 0.5 0.25 0.13
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
-4
-2
2
4
6
5
4
3
2
1
h
x
(
)
=
3
x
不同底的图像的特征
6
5
4
3
2
1
-4
-2
2
4
q
x
(
)
=( )
1
3
x
不同底的图像的特征
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
普通高中课程标准实验教科书《数学》必修1
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
请同学们结合图像特征思考以下问题:
1、图像分布在哪些象限,与x轴的相对位置关系如何?
2、图象关于原点对称吗?关于y轴对称吗?
3、函数图象过定点吗?
4、自左向右看,图象上升(下降)的趋势是怎样的?
5、在第一象限内的图象纵坐标具有什么特点?
6、在第二象限内的图象纵坐标具有什么特点?
图象特征 函数性质
向x轴正负方向无限延伸
函数的定义域为R
函数图象都在x轴上方
函数的值域为全体正实数
图象关于原点和y轴不对称
非奇非偶函数
函数图象都过定点(0,1)
自左向右看,
图象逐渐上升
在R上是增函数
自左向右看,
图象逐渐下降
在R上是减函数
在第二象限内的图
象纵坐标都小于1
在第一象限内的图
象纵坐标都小于1
在第一象限内的图
象纵坐标都大于1
在第二象限内的图
象纵坐标都大于1
思考:底数的变化会对图像产生什么影响
理论迁移
指数函数
例:已知指数函数
的图像经过点(3,π),求f(0),
f(1),f(-3)
解:因为f(x)=ax的图像经过点(3,π),
所以
f (3)=π,解得a=
,f(x)=
指数函数
理论迁移
例2:比较大小:
(1)
解:因为f(x)=1.7x在R上是增函数,
且2.5 < 3,
所以1.7 2.5< 1.73 。
1.72.5 ,1.73
1.7x
指数函数
理论迁移
例2:比较大小:
(2) 0.8-0.1,0.8-0.2
解:因为f(x)=0.8x在R上是减函数,
且-0.1>-0.2,
所以0.8-0.1 < 0.8-0.2。
0.8x
指数函数
理论迁移
例2:比较大小:
(3)1.7 0.3,0.93.1
解:由指数函数的性质知1.70.3 > 1.70 =1,而
0.93.1 < 0.90 =1
所以
1.70.3 > 0.93.1
y=13×(1+1%)x =13 ×1.01x
当x=20时,y= 13 ×1.0120≈16(亿)
所以经过20年后,我国人口最多为16亿。
截止到1999年底,我国人口约13亿,如果能将人口年平均增长率控制在1%,那么经过20年后我国的人口数最多为多少(精确到亿)?
在实际问题中,经常会遇到类似的指数增长模型:
设原有量为N,每次的增长率为P,经过X次增长,该量增长到Y,则
Y=N(1+P)X
形如y=kax的函数是一种指数型函数,这是非常有用的函数模型。
考古中的指数函数
知识扩展
含C物质的C-14含量在C元素中所含的比例几乎是保持恒定的,如果含C物质一旦停止与大气的交换关系,则该物质的C-14含量不在得到新的补充,而原有的C-14按照衰变规律减少,每隔5730年减少一半,因此只要测出含C物质中C-14的减少的程度,就可以计算出它停止与大气进行交换的年代,这就是C-14测年的原理。
测年方法进入考古学研究被誉为考古学发展史上的一次革命,它将考古学研究中得到的相对年代转变为绝对年代,给考古学带来了质的飞跃,使研究更加科学化,促进了考古学研究的深入。其中测算公式是一个指数式。
安阳曹操墓是真是假?
魏武帝曹操(公元155~220)
1、指数函数的定义;
2、指数函数图象的作法;
3、指数函数的图象和性质.
小 结
函数 叫做指数函数,其中x是自变量.
列表 描点 连线
图
象
性
质
(1)定义域
(2)值域
(3)定点
(5)函数值的分布情况
(4)单调性
x
y
o
1
x
y
o
1
R
( 0 , + ∞)
过定点 ( 0 , 1 ),即x=0时,y=1
当x>0时,y>1
当x<0时,0<y<1
当x>0时, 0<y<1
当x<0时, y>1
在R上是增函数
在R上是减函数
a > 1
0 < a < 1
3.指数函数的图象和性质
作业:
教科书P59,习题2.1A组
5,6,7,8,9
谢谢各位老师和同学们!
再见!
百年南山,百年经典
