四年级下册数学课件-7.10 多边形的内角和苏教版 25张ppt
文档属性
| 名称 | 四年级下册数学课件-7.10 多边形的内角和苏教版 25张ppt |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
“没有大胆的猜想,
就做不出伟大的发现。”
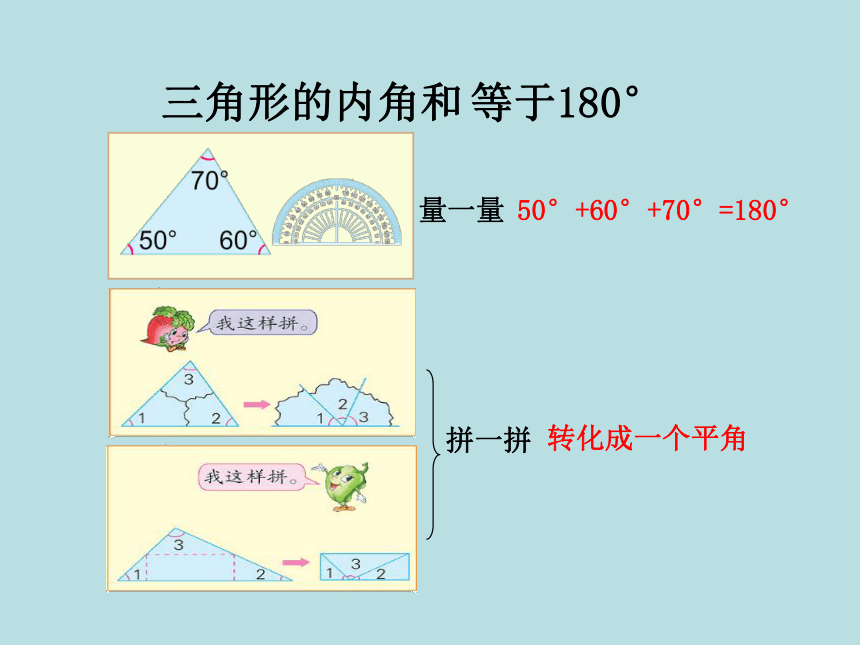
等于180°
三角形的内角和
量一量
拼一拼
转化成一个平角
等于180°
50°+60°+70°=180°
三角形的内角和
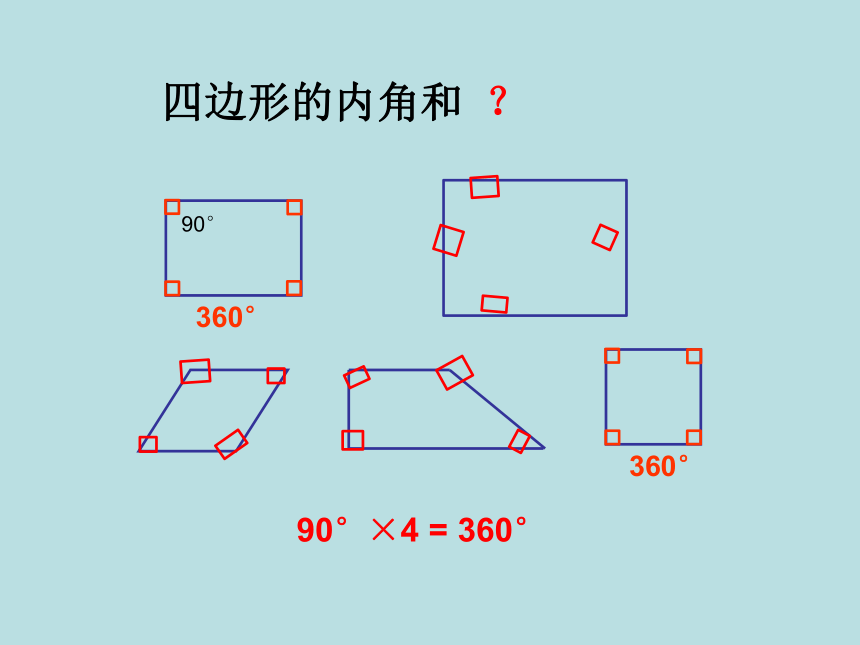
360°
360°
90°
90°×4
=
360°
四边形的内角和
?
360°
360°
90°
用你喜欢的方法验证四边形的内角和。
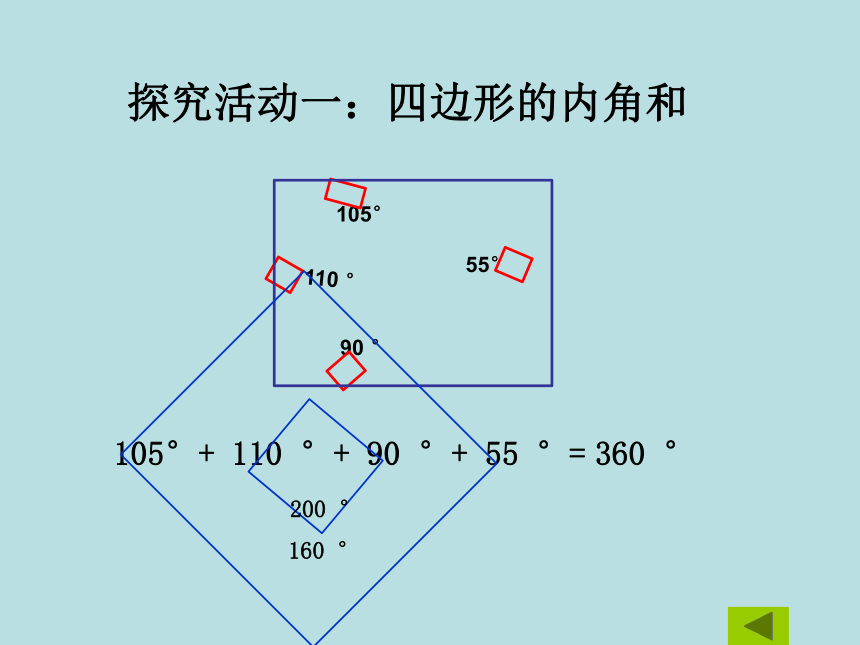
探究活动一:四边形的内角和
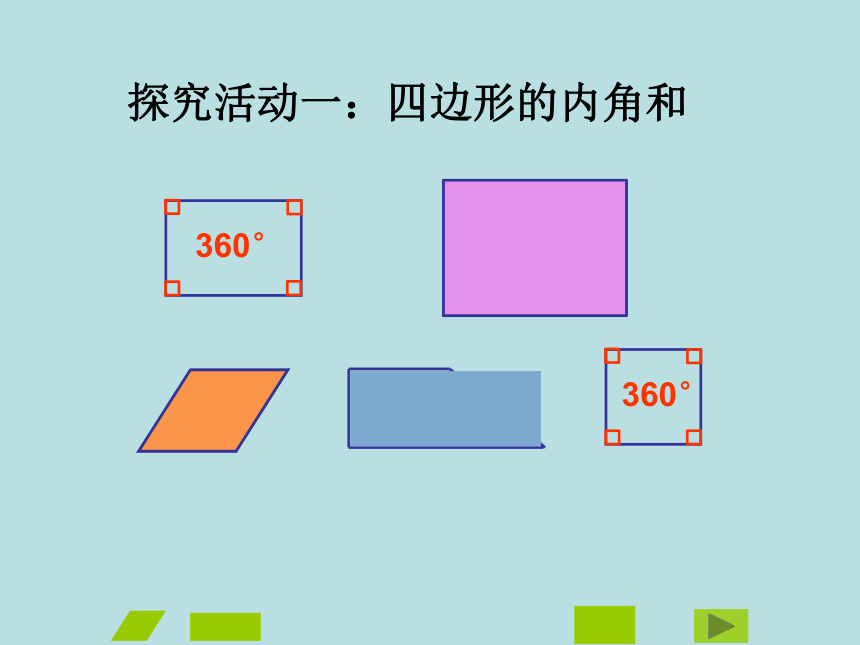
360°
360°
探究活动一:四边形的内角和
90
°
110
°
105°
55°
105°+
110
°+
90
°+
55
°=
360
°
探究活动一:四边形的内角和
200
°
160
°
探究活动一:四边形的内角和
180°
180°
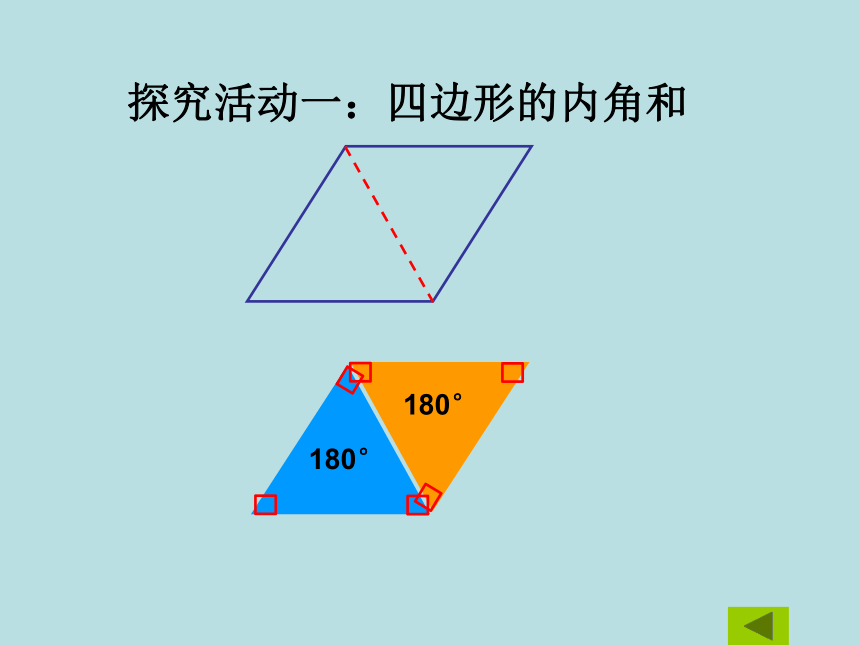
探究活动一:四边形的内角和
180°
180°
探究活动一:四边形的内角和
180°
180°
探究活动一:四边形的内角和
180°
180°
180°×
2
=
360
°
探究活动一:四边形的内角和
①
②
180°×
2
=
360
°
①
②
①
②
①
②
①
②
探究活动一:四边形的内角和
360°
180°×
2
=
360
°
探究活动一:四边形的内角和
360°
360°
①
②
①
②
①
②
③
③
③
180°×
3
=
540
°
探究活动二:五边形的内角和
540°
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
四边形
五边形
六边形
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
●
720°
180°×
4
=
720
°
从简单的问题想起、有序思考,是探索规律的有效方法
可以把新的问题转化成能够解决的问题
多边形的内角和可以根据三角形的内角和推算出来
回顾探索和发现规律的过程,说说你的体会。
小试牛刀
剪一刀能得到一个几边形,内角和是多少度?
三角形
内角和是180°
四边形
内角和是360°
五边形
内角和是540°
图形变变变
180°
360°
图形变变变
180°
360°
180°
360°
540°
1080°
1080÷180
6
+
2
=
8
=
6
图形变变变
360°
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
①
③
②
④
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
①
②
③
④
720°
180°×
4
=
720
°
●
“没有大胆的猜想,
就做不出伟大的发现。”
等于180°
三角形的内角和
量一量
拼一拼
转化成一个平角
等于180°
50°+60°+70°=180°
三角形的内角和
360°
360°
90°
90°×4
=
360°
四边形的内角和
?
360°
360°
90°
用你喜欢的方法验证四边形的内角和。
探究活动一:四边形的内角和
360°
360°
探究活动一:四边形的内角和
90
°
110
°
105°
55°
105°+
110
°+
90
°+
55
°=
360
°
探究活动一:四边形的内角和
200
°
160
°
探究活动一:四边形的内角和
180°
180°
探究活动一:四边形的内角和
180°
180°
探究活动一:四边形的内角和
180°
180°
探究活动一:四边形的内角和
180°
180°
180°×
2
=
360
°
探究活动一:四边形的内角和
①
②
180°×
2
=
360
°
①
②
①
②
①
②
①
②
探究活动一:四边形的内角和
360°
180°×
2
=
360
°
探究活动一:四边形的内角和
360°
360°
①
②
①
②
①
②
③
③
③
180°×
3
=
540
°
探究活动二:五边形的内角和
540°
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
四边形
五边形
六边形
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
●
720°
180°×
4
=
720
°
从简单的问题想起、有序思考,是探索规律的有效方法
可以把新的问题转化成能够解决的问题
多边形的内角和可以根据三角形的内角和推算出来
回顾探索和发现规律的过程,说说你的体会。
小试牛刀
剪一刀能得到一个几边形,内角和是多少度?
三角形
内角和是180°
四边形
内角和是360°
五边形
内角和是540°
图形变变变
180°
360°
图形变变变
180°
360°
180°
360°
540°
1080°
1080÷180
6
+
2
=
8
=
6
图形变变变
360°
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
①
③
②
④
探究活动三:六边形的内角和
①
②
③
④
①
②
③
④
①
②
③
④
720°
180°×
4
=
720
°
●
