2021-2022学年华东师大版九年级数学上册23.6.2图形的变换与坐标课时作业(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册23.6.2图形的变换与坐标课时作业(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 266.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 08:11:02 | ||
图片预览



文档简介
23.6.2 图形的变换与坐标
知识点
1 平移变换与坐标变化
1.[2020·泸州]
在平面直角坐标系中,将点A(-2,3)向右平移4个单位,得到的对应点A'的坐标为
( )
A.(2,7)
B.(-6,3)
C.(2,3)
D.(-2,-1)
2.[2019·滨州]
在平面直角坐标系中,将点A(1,-2)向上平移3个单位,再向左平移2个单位,得到点B,则点B的坐标是
( )
A.(-1,1)
B.(3,1)
C.(4,-4)
D.(4,0)
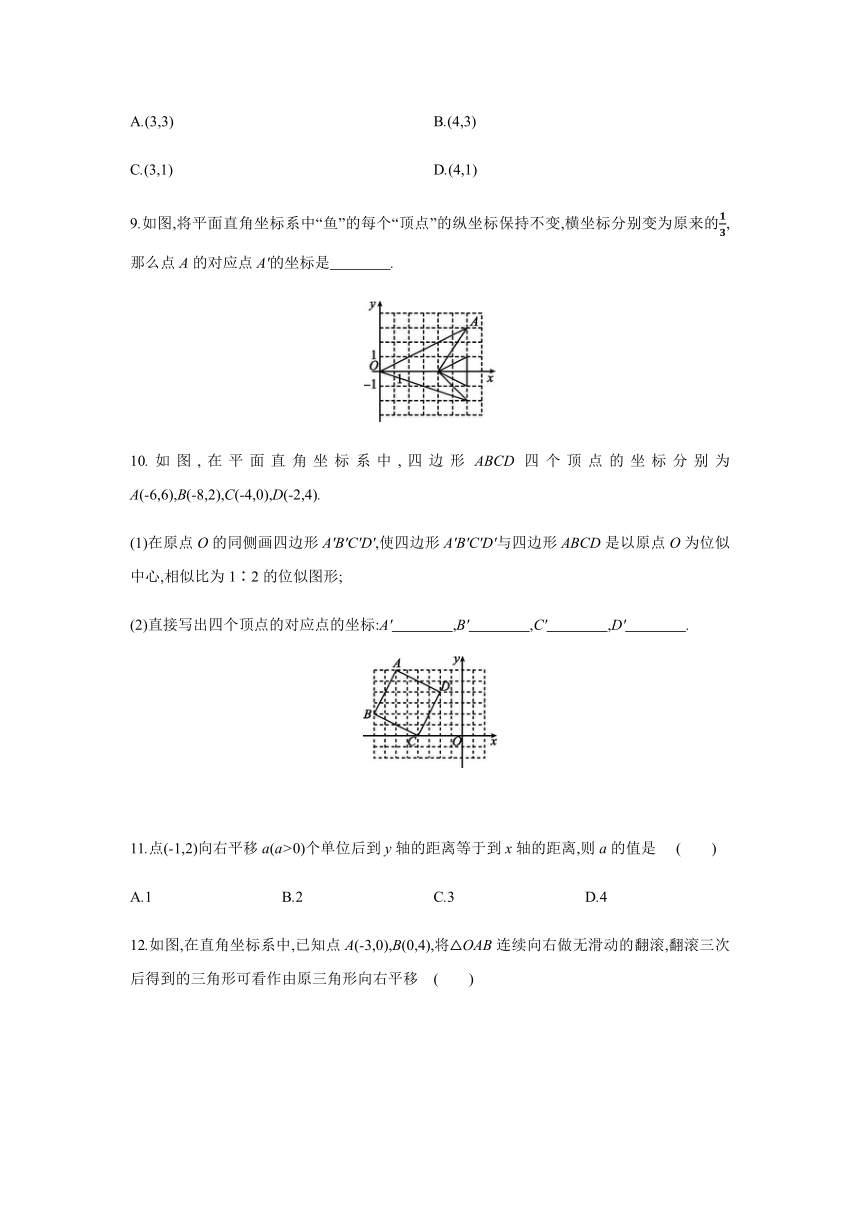
3.[2019·海南]
如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为
( )
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
4.[2020·台州]
如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)的对应点的坐标为
( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
知识点
2 对称变换与坐标变化
5.[教材练习第1题变式]
如图,如果作出△ABC关于x轴的轴对称图形△A'B'C',那么所得各点坐标分别是A' ,B' ,C' .?
6.如图,在平面直角坐标系中,直线m经过点(1,0),且垂直于x轴,则点P(-1,2)关于直线m的对称点的坐标为 .?
7.在平面直角坐标系中,将△ABC的三个顶点,
(1)横坐标都乘以-1,纵坐标不变,则所得三角形与原三角形关于 对称;?
(2)纵坐标都乘以-1,横坐标不变,则所得三角形与原三角形关于 对称;?
(3)横、纵坐标都乘以-1,则所得三角形与原三角形关于 对称.?
知识点
3 位似变换与坐标变化
8.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2).以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为
( )
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
9.如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别变为原来的,那么点A的对应点A'的坐标是 .?
10.如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4).
(1)在原点O的同侧画四边形A'B'C'D',使四边形A'B'C'D'与四边形ABCD是以原点O为位似中心,相似比为1∶2的位似图形;
(2)直接写出四个顶点的对应点的坐标:A' ,B' ,C' ,D' .?
11.点(-1,2)向右平移a(a>0)个单位后到y轴的距离等于到x轴的距离,则a的值是
( )
A.1
B.2
C.3
D.4
12.如图,在直角坐标系中,已知点A(-3,0),B(0,4),将△OAB连续向右做无滑动的翻滚,翻滚三次后得到的三角形可看作由原三角形向右平移
( )
A.9个单位
B.12个单位
C.15个单位
D.7个单位
13.如图,在平面直角坐标系中,△ABC与△DEF关于直线m:x=1对称,点M,N是这两个三角形中的一组对应点,如果点M的横坐标是a,那么点N的横坐标是 .?
14.若点A(-1,-1)是平面直角坐标系内的点,将点A向右平移2个单位,再向上平移2个单位,再向左平移2个单位,再向下平移2个单位……如此平移下去,则经过第2021次平移后的坐标为 .?
15.如图,在边长为1的小正方形组成的网格中建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是
.?
16.已知:如图,△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).
(1)画出△ABC向下平移4个单位得到的△A1B1C1;
(2)以点B为位似中心,在点B的同侧画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为2∶1;
(3)△A3B3C3与△A1B1C1是位似图形,位似中心为原点,相似比为3∶2,若M1(a,b)为线段A1C1上任意一点,写出点M1的对应点M2的坐标.
17.如图,在平面直角坐标系中,△ABO的顶点坐标分别为O(0,0),A(2a,0),B(0,-a),线段EF两端点的坐标分别为E(-m,a+1),F(-m,1)(2a>m>a).直线l∥y轴交x轴于点P(a,0),且线段EF与CD关于y轴对称,线段CD与MN关于直线l对称.
(1)求点M,N的坐标(用含m,a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?请你说明理由.若能,请你写出一个平移方案(平移的单位数用m,a表示).
教师详解详析
1.C
2.A [解析]
∵将点A(1,-2)向上平移3个单位,再向左平移2个单位,得到点B,∴点B的横坐标为1-2=-1,纵坐标为-2+3=1,∴点B的坐标为(-1,1).
故选A.
3.C [解析]
由点A(2,1)平移后得到点A1(-2,2),可得线段的平移规律是:左移4个单位,上移1个单位,
∴点B(3,-1)的对应点B1的坐标为(-1,0).
故选C.
4.D
5.(1,-3) (4,-1) (1,-1)
6.(3,2) [解析]
点P关于直线x=1的对称点的纵坐标与点P的纵坐标相等,且两点到直线x=1的距离相等,据此可得其横坐标.
7.(1)y轴
(2)x轴
(3)坐标原点
8.A [解析]
∵点C是点A的对应点,相似比是,点C在第一象限,
∴点C的坐标为(6×,6×),即(3,3).
故选A.
9.(2,3) [解析]
点A变化前的坐标为(6,3),将点A的纵坐标保持不变,横坐标变为原来的,得到点A的对应点A'的坐标是(2,3).故答案为(2,3).
10.解:(1)如图,四边形A'B'C'D'即为所求.
(2)(-3,3) (-4,1) (-2,0) (-1,2)
11.C [解析]
点(-1,2)向右平移a(a>0)个单位后的对应点坐标为(-1+a,2).
∵点(-1,2)向右平移a(a>0)个单位后到y轴的距离等于到x轴的距离,
∴|-1+a|=|2|,解得a=3或a=-1.
∵a>0,∴a=3.故选C.
12.B [解析]
∵点A(-3,0),B(0,4),∴OB=4,OA=3,∴AB==5.∵将△OAB连续向右做无滑动的翻滚,翻滚三次后回到原来的状态,∴翻滚三次后得到的三角形可看作由原三角形向右平移了3+4+5=12(个)单位.故选B.
13.2-a
14.(1,-1) [解析]
由平移的特征知第1次平移后的坐标为(1,-1),第2次平移后的坐标为(1,1),第3次平移后的坐标为(-1,1),第4次平移后的坐标为(-1,-1),第5次平移后的坐标为(1,-1)……于是知道平移后的坐标为四次一个循环.而2021÷4=505……1,因此第2021次平移后的坐标与第1次平移后的坐标相同,为(1,-1).
15.(4,2)或(-4,-2)
[解析]
如图所示,△A1B1C1和△A'B'C'与△ABC的相似比均为2,故点B的对应点的坐标是(4,2)或(-4,-2).
16.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)点M1的对应点M2的坐标为(a,b)或(-a,-b).
17.解:(1)∵EF与CD关于y轴对称,EF两端点的坐标分别为E(-m,a+1),F(-m,1),
∴C(m,a+1),D(m,1).
设CD与直线l之间的距离为x.
∵CD与MN关于直线l对称,l与y轴之间的距离为a,
∴MN与y轴之间的距离为a-x.
∵x=m-a,
∴点M的横坐标为a-(m-a)=2a-m,
∴M(2a-m,a+1),N(2a-m,1).
(2)能重合.
理由:∵EM=2a-m-(-m)=2a=OA,EF=a+1-1=a=OB,且EF∥y轴,EM∥x轴,
∴∠MEF=∠AOB=90°,
∴△MFE≌△ABO,
∴△ABO与△MFE通过平移能重合.
平移方案:将△ABO向上平移(a+1)个单位后,再向左平移m个单位,即可与△MFE重合.(平移方案不唯一)
知识点
1 平移变换与坐标变化
1.[2020·泸州]
在平面直角坐标系中,将点A(-2,3)向右平移4个单位,得到的对应点A'的坐标为
( )
A.(2,7)
B.(-6,3)
C.(2,3)
D.(-2,-1)
2.[2019·滨州]
在平面直角坐标系中,将点A(1,-2)向上平移3个单位,再向左平移2个单位,得到点B,则点B的坐标是
( )
A.(-1,1)
B.(3,1)
C.(4,-4)
D.(4,0)
3.[2019·海南]
如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为
( )
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
4.[2020·台州]
如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)的对应点的坐标为
( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
知识点
2 对称变换与坐标变化
5.[教材练习第1题变式]
如图,如果作出△ABC关于x轴的轴对称图形△A'B'C',那么所得各点坐标分别是A' ,B' ,C' .?
6.如图,在平面直角坐标系中,直线m经过点(1,0),且垂直于x轴,则点P(-1,2)关于直线m的对称点的坐标为 .?
7.在平面直角坐标系中,将△ABC的三个顶点,
(1)横坐标都乘以-1,纵坐标不变,则所得三角形与原三角形关于 对称;?
(2)纵坐标都乘以-1,横坐标不变,则所得三角形与原三角形关于 对称;?
(3)横、纵坐标都乘以-1,则所得三角形与原三角形关于 对称.?
知识点
3 位似变换与坐标变化
8.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2).以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为
( )
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
9.如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别变为原来的,那么点A的对应点A'的坐标是 .?
10.如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4).
(1)在原点O的同侧画四边形A'B'C'D',使四边形A'B'C'D'与四边形ABCD是以原点O为位似中心,相似比为1∶2的位似图形;
(2)直接写出四个顶点的对应点的坐标:A' ,B' ,C' ,D' .?
11.点(-1,2)向右平移a(a>0)个单位后到y轴的距离等于到x轴的距离,则a的值是
( )
A.1
B.2
C.3
D.4
12.如图,在直角坐标系中,已知点A(-3,0),B(0,4),将△OAB连续向右做无滑动的翻滚,翻滚三次后得到的三角形可看作由原三角形向右平移
( )
A.9个单位
B.12个单位
C.15个单位
D.7个单位
13.如图,在平面直角坐标系中,△ABC与△DEF关于直线m:x=1对称,点M,N是这两个三角形中的一组对应点,如果点M的横坐标是a,那么点N的横坐标是 .?
14.若点A(-1,-1)是平面直角坐标系内的点,将点A向右平移2个单位,再向上平移2个单位,再向左平移2个单位,再向下平移2个单位……如此平移下去,则经过第2021次平移后的坐标为 .?
15.如图,在边长为1的小正方形组成的网格中建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是
.?
16.已知:如图,△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).
(1)画出△ABC向下平移4个单位得到的△A1B1C1;
(2)以点B为位似中心,在点B的同侧画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为2∶1;
(3)△A3B3C3与△A1B1C1是位似图形,位似中心为原点,相似比为3∶2,若M1(a,b)为线段A1C1上任意一点,写出点M1的对应点M2的坐标.
17.如图,在平面直角坐标系中,△ABO的顶点坐标分别为O(0,0),A(2a,0),B(0,-a),线段EF两端点的坐标分别为E(-m,a+1),F(-m,1)(2a>m>a).直线l∥y轴交x轴于点P(a,0),且线段EF与CD关于y轴对称,线段CD与MN关于直线l对称.
(1)求点M,N的坐标(用含m,a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?请你说明理由.若能,请你写出一个平移方案(平移的单位数用m,a表示).
教师详解详析
1.C
2.A [解析]
∵将点A(1,-2)向上平移3个单位,再向左平移2个单位,得到点B,∴点B的横坐标为1-2=-1,纵坐标为-2+3=1,∴点B的坐标为(-1,1).
故选A.
3.C [解析]
由点A(2,1)平移后得到点A1(-2,2),可得线段的平移规律是:左移4个单位,上移1个单位,
∴点B(3,-1)的对应点B1的坐标为(-1,0).
故选C.
4.D
5.(1,-3) (4,-1) (1,-1)
6.(3,2) [解析]
点P关于直线x=1的对称点的纵坐标与点P的纵坐标相等,且两点到直线x=1的距离相等,据此可得其横坐标.
7.(1)y轴
(2)x轴
(3)坐标原点
8.A [解析]
∵点C是点A的对应点,相似比是,点C在第一象限,
∴点C的坐标为(6×,6×),即(3,3).
故选A.
9.(2,3) [解析]
点A变化前的坐标为(6,3),将点A的纵坐标保持不变,横坐标变为原来的,得到点A的对应点A'的坐标是(2,3).故答案为(2,3).
10.解:(1)如图,四边形A'B'C'D'即为所求.
(2)(-3,3) (-4,1) (-2,0) (-1,2)
11.C [解析]
点(-1,2)向右平移a(a>0)个单位后的对应点坐标为(-1+a,2).
∵点(-1,2)向右平移a(a>0)个单位后到y轴的距离等于到x轴的距离,
∴|-1+a|=|2|,解得a=3或a=-1.
∵a>0,∴a=3.故选C.
12.B [解析]
∵点A(-3,0),B(0,4),∴OB=4,OA=3,∴AB==5.∵将△OAB连续向右做无滑动的翻滚,翻滚三次后回到原来的状态,∴翻滚三次后得到的三角形可看作由原三角形向右平移了3+4+5=12(个)单位.故选B.
13.2-a
14.(1,-1) [解析]
由平移的特征知第1次平移后的坐标为(1,-1),第2次平移后的坐标为(1,1),第3次平移后的坐标为(-1,1),第4次平移后的坐标为(-1,-1),第5次平移后的坐标为(1,-1)……于是知道平移后的坐标为四次一个循环.而2021÷4=505……1,因此第2021次平移后的坐标与第1次平移后的坐标相同,为(1,-1).
15.(4,2)或(-4,-2)
[解析]
如图所示,△A1B1C1和△A'B'C'与△ABC的相似比均为2,故点B的对应点的坐标是(4,2)或(-4,-2).
16.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)点M1的对应点M2的坐标为(a,b)或(-a,-b).
17.解:(1)∵EF与CD关于y轴对称,EF两端点的坐标分别为E(-m,a+1),F(-m,1),
∴C(m,a+1),D(m,1).
设CD与直线l之间的距离为x.
∵CD与MN关于直线l对称,l与y轴之间的距离为a,
∴MN与y轴之间的距离为a-x.
∵x=m-a,
∴点M的横坐标为a-(m-a)=2a-m,
∴M(2a-m,a+1),N(2a-m,1).
(2)能重合.
理由:∵EM=2a-m-(-m)=2a=OA,EF=a+1-1=a=OB,且EF∥y轴,EM∥x轴,
∴∠MEF=∠AOB=90°,
∴△MFE≌△ABO,
∴△ABO与△MFE通过平移能重合.
平移方案:将△ABO向上平移(a+1)个单位后,再向左平移m个单位,即可与△MFE重合.(平移方案不唯一)
