2020-2021学年人教版数学八年级上册11.1.1探究三角形三边关系课件(25张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.1.1探究三角形三边关系课件(25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览







文档简介
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
第十一章 三角形
新人教版—八年级(上)数学
11.1.1 三角形的边
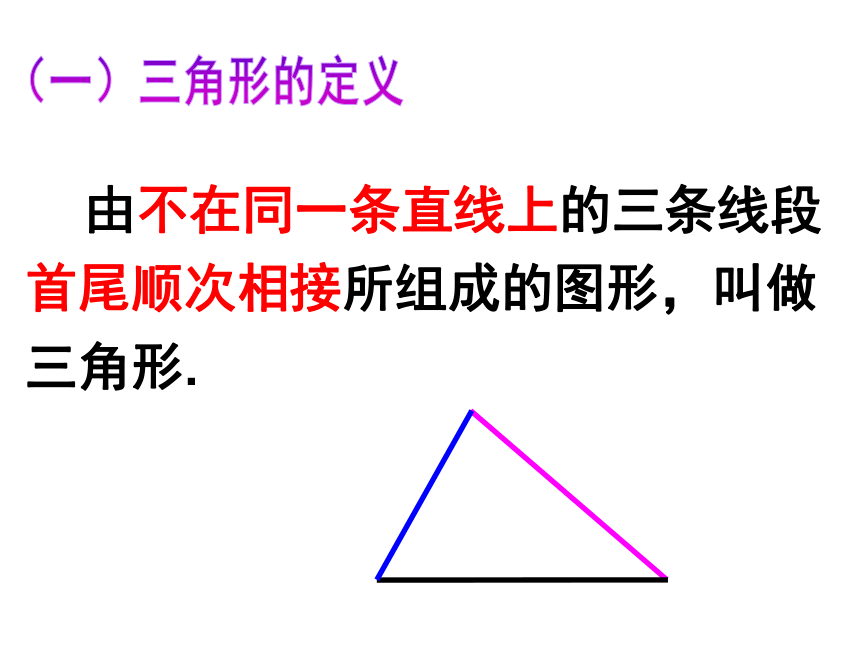
问题1 什么样的图形叫做三角形?
由不在同一条直线上的三条线段
首尾顺次相接所组成的图形,叫做
三角形.
练习1:下列图形中,哪个是三角形?
(1) (2) (3)
(4) (5) (6)
读一读:阅读课本第2页的第3~5段,
自学三角形以及三角形的顶点、边、
角的表示方法.
C
A
B
记作:△ABC
顶点:点A,点B,点C
边:AB,BC,AC
( 或c,a,b )
角:∠A,∠B,∠C
a
c
b
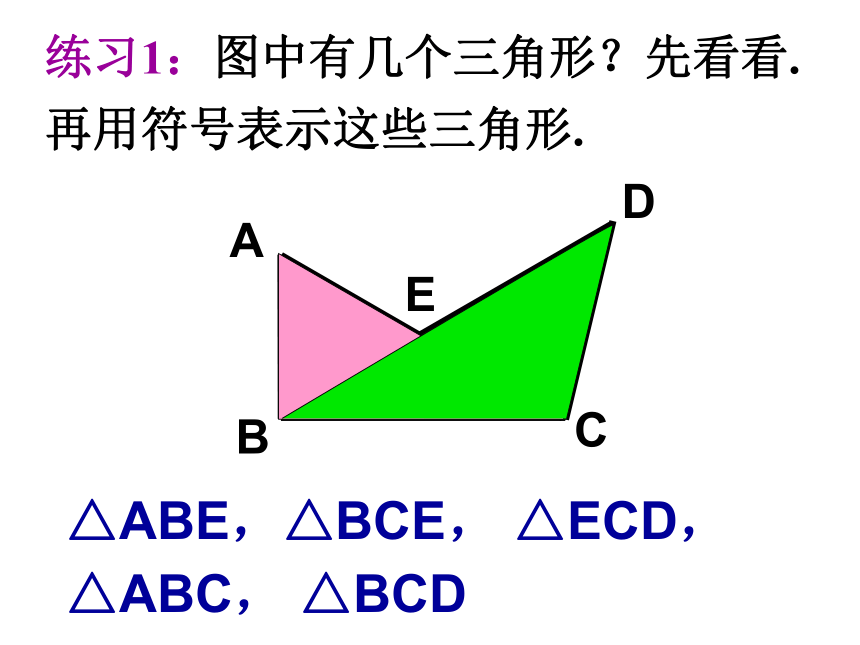
练习2:图中有几个三角形?先看看.
再用符号表示这些三角形.
A
D
B
E
C
△ABE,△BCE, △ECD,
△ABC, △BCD
A
D
B
E
C
(1) (2) (3)
(4) (5)
6
6
6
6
6
9
15
6
8
8
6
12
问题2 你能将这些三角形分类吗?
你是按什么标准来分类的?
腰
腰
底边
顶角
底角
底角
等腰三角形:有两边相等的三角形
底边=腰
直角三角形
按边分
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
锐角三角形
钝角三角形
按角分
钝角三角形
直角三角形
锐角三角形
按边分
三边都
不相等
的三角形
等边
三角形
等腰三角形
他一步能走3米,你相信吗?
(姚明腿长1.28米)
A
B
C
1.28
1.28
3?
数学活动
以四人小组为单位,选取小彩棒
分别拼成三条线段,再尝试将这三条
线段摆成三角形,并填写活动单:
操作
次数
能否摆成三角形
线段
的长
线段
的长
线段
的长
操作:
观察:
●
●
●
A
B
C
AC + CB ___AB
CB + AB ___AC
AB + AC ___CB
>
>
>
理由:两点之间,线段最短.
三角形两边之和大于第三边.
猜想:
三角形两边之和大于第三边.
三角形两边之差小于第三边.
●
●
●
A
B
C
(1) 5,6,10;
(2) 5,6,11;
(3) 3,4,8;
(2) ∵5+6=11,
∴这三条线段不能组成一个三角形.
∵5+6>10,
∴这三条线段能组成一个三角形.
解:
练习3:下列长度的三条线段能否组成三角形?为什么?
技巧:
只需检查较小的两条线段之和
是否大于第三条线段.
他一步能走3米,你相信吗?
(姚明腿长1.28米)
A
B
C
1.28
1.28
3?
分类讨论思想
三角形的定义
三角形的表示方法
三角形的分类、三边关系
三角形三边关系的应用
定义
表示方法
性质
应用
几
何
图
形
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
第十一章 三角形
新人教版 数学 八年级(上)
11.1.1 三角形的边
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
第十一章 三角形
新人教版 数学 八年级(上)
11.1.1 三角形的边
问题1 你能用自己的语言说一说,
什么样的图形叫做三角形吗?
拼一拼:你能用三条线段拼出三角形吗?
由不在同一条直线上的三条线段
首尾顺次相接所组成的图形,叫做
三角形.
腰
腰
底边
等腰三角形:有两边相等的三角形
底边=腰
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
练习1:图中有几个三角形?先看看.
再用符号表示这些三角形.
A
D
B
E
C
△ABE,△BCE, △ECD,
△ABC, △BCD
(1) (2) (3)
(4) (5)
6
6
6
6
6
9
15
6
8
8
6
12
问题2 你能将这些三角形分类吗?
你是按什么标准来分类的?
按角分
钝角三角形
直角三角形
锐角三角形
按边分
三边都
不相等
的三角形
等边
三角形
等腰三角形
他一步能走3米,你相信吗?
(姚明腿长1.28米)
A
B
C
1.28
1.28
3?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
●
●
●
A
B
C
AC + CB ___AB
CB + AB ___AC
AB + AC ___CB
>
>
>
理由:两点之间,线段最短.
三角形两边之和大于第三边.
猜想:
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
理由:两点之间,线段最短.
三角形两边之和大于第三边.
猜想:
数学语言:
问题3 三角形两边的差与第三边
有什么关系?
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
AB-CB <AC
AC-AB <CB
CB-AC <AB
分类讨论思想
(1)设底边长为 x cm,则腰长为2xcm,
x+2x+2x=18
解得
x=3.6
解:
∴ 三边长分别为3.6cm,7.2cm,7.2cm.
三角形的定义
三角形的表示方法
三角形的分类、三边关系
三角形三边关系的应用
定义
表示方法
性质
应用
几
何
图
形
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
三角形的定义
三角形的表示方法
三角形的分类、三边关系
三角形三边关系的应用
定义
表示方法
性质
应用
几
何
图
形
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
(1) 5,6,10;
(2) 5,6,11;
(3) 3,4,8;
(2) ∵5+6=11,
∴这三条线段不能组成一个三角形.
∵5+6>10,
∴这三条线段能组成一个三角形.
解:
练习2:下列长度的三条线段能否组成三角形?为什么?
技巧:
只需检查较小的两条线段之和
是否大于第三条线段.
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
姚明腿长1.28米,他一步能走3米,
你相信吗?
A
B
C
1.28
1.28
3?
问题3 三角形两边的差与第三边
有什么关系?
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
AB-CB <AC
AC-AB <CB
CB-AC <AB
A
B
C
1.28
1.28
3?
姚明腿长1.28米,他一步能走3米,
你相信吗?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
(1) (2) (3)
(4) (5)
6
6
6
6
6
9
15
6
8
8
6
12
问题2 你能将这些三角形分类吗?
你是按什么标准来分类的?
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
第十一章 三角形
新人教版—八年级(上)数学
11.1.1 三角形的边
问题1 什么样的图形叫做三角形?
由不在同一条直线上的三条线段
首尾顺次相接所组成的图形,叫做
三角形.
练习1:下列图形中,哪个是三角形?
(1) (2) (3)
(4) (5) (6)
读一读:阅读课本第2页的第3~5段,
自学三角形以及三角形的顶点、边、
角的表示方法.
C
A
B
记作:△ABC
顶点:点A,点B,点C
边:AB,BC,AC
( 或c,a,b )
角:∠A,∠B,∠C
a
c
b
练习2:图中有几个三角形?先看看.
再用符号表示这些三角形.
A
D
B
E
C
△ABE,△BCE, △ECD,
△ABC, △BCD
A
D
B
E
C
(1) (2) (3)
(4) (5)
6
6
6
6
6
9
15
6
8
8
6
12
问题2 你能将这些三角形分类吗?
你是按什么标准来分类的?
腰
腰
底边
顶角
底角
底角
等腰三角形:有两边相等的三角形
底边=腰
直角三角形
按边分
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
锐角三角形
钝角三角形
按角分
钝角三角形
直角三角形
锐角三角形
按边分
三边都
不相等
的三角形
等边
三角形
等腰三角形
他一步能走3米,你相信吗?
(姚明腿长1.28米)
A
B
C
1.28
1.28
3?
数学活动
以四人小组为单位,选取小彩棒
分别拼成三条线段,再尝试将这三条
线段摆成三角形,并填写活动单:
操作
次数
能否摆成三角形
线段
的长
线段
的长
线段
的长
操作:
观察:
●
●
●
A
B
C
AC + CB ___AB
CB + AB ___AC
AB + AC ___CB
>
>
>
理由:两点之间,线段最短.
三角形两边之和大于第三边.
猜想:
三角形两边之和大于第三边.
三角形两边之差小于第三边.
●
●
●
A
B
C
(1) 5,6,10;
(2) 5,6,11;
(3) 3,4,8;
(2) ∵5+6=11,
∴这三条线段不能组成一个三角形.
∵5+6>10,
∴这三条线段能组成一个三角形.
解:
练习3:下列长度的三条线段能否组成三角形?为什么?
技巧:
只需检查较小的两条线段之和
是否大于第三条线段.
他一步能走3米,你相信吗?
(姚明腿长1.28米)
A
B
C
1.28
1.28
3?
分类讨论思想
三角形的定义
三角形的表示方法
三角形的分类、三边关系
三角形三边关系的应用
定义
表示方法
性质
应用
几
何
图
形
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
第十一章 三角形
新人教版 数学 八年级(上)
11.1.1 三角形的边
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
第十一章 三角形
新人教版 数学 八年级(上)
11.1.1 三角形的边
问题1 你能用自己的语言说一说,
什么样的图形叫做三角形吗?
拼一拼:你能用三条线段拼出三角形吗?
由不在同一条直线上的三条线段
首尾顺次相接所组成的图形,叫做
三角形.
腰
腰
底边
等腰三角形:有两边相等的三角形
底边=腰
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
练习1:图中有几个三角形?先看看.
再用符号表示这些三角形.
A
D
B
E
C
△ABE,△BCE, △ECD,
△ABC, △BCD
(1) (2) (3)
(4) (5)
6
6
6
6
6
9
15
6
8
8
6
12
问题2 你能将这些三角形分类吗?
你是按什么标准来分类的?
按角分
钝角三角形
直角三角形
锐角三角形
按边分
三边都
不相等
的三角形
等边
三角形
等腰三角形
他一步能走3米,你相信吗?
(姚明腿长1.28米)
A
B
C
1.28
1.28
3?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
●
●
●
A
B
C
AC + CB ___AB
CB + AB ___AC
AB + AC ___CB
>
>
>
理由:两点之间,线段最短.
三角形两边之和大于第三边.
猜想:
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
理由:两点之间,线段最短.
三角形两边之和大于第三边.
猜想:
数学语言:
问题3 三角形两边的差与第三边
有什么关系?
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
AB-CB <AC
AC-AB <CB
CB-AC <AB
分类讨论思想
(1)设底边长为 x cm,则腰长为2xcm,
x+2x+2x=18
解得
x=3.6
解:
∴ 三边长分别为3.6cm,7.2cm,7.2cm.
三角形的定义
三角形的表示方法
三角形的分类、三边关系
三角形三边关系的应用
定义
表示方法
性质
应用
几
何
图
形
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
三角形的定义
三角形的表示方法
三角形的分类、三边关系
三角形三边关系的应用
定义
表示方法
性质
应用
几
何
图
形
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
(1) 5,6,10;
(2) 5,6,11;
(3) 3,4,8;
(2) ∵5+6=11,
∴这三条线段不能组成一个三角形.
∵5+6>10,
∴这三条线段能组成一个三角形.
解:
练习2:下列长度的三条线段能否组成三角形?为什么?
技巧:
只需检查较小的两条线段之和
是否大于第三条线段.
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
姚明腿长1.28米,他一步能走3米,
你相信吗?
A
B
C
1.28
1.28
3?
问题3 三角形两边的差与第三边
有什么关系?
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
AB-CB <AC
AC-AB <CB
CB-AC <AB
A
B
C
1.28
1.28
3?
姚明腿长1.28米,他一步能走3米,
你相信吗?
按角分
例 用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为 4 cm的等腰三角形吗?为什么?
(1) (2) (3)
(4) (5)
6
6
6
6
6
9
15
6
8
8
6
12
问题2 你能将这些三角形分类吗?
你是按什么标准来分类的?
