2020-2021学年人教版数学八年级上册11.2.2三角形的外角2课件(精选)(共21张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.2.2三角形的外角2课件(精选)(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 320.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览




文档简介
旧知回顾
1.三角形的内角和定理的内容
2、在ABC中,
(1)若∠C=90°,∠A=30 ° ,则∠B= ;
65°
60°
(2)若∠A=50 ° ,∠B=∠C,则∠B= .
旧知回顾
3、在△ABC中,
若∠A:∠B:∠C=2:3:4,则∠A= ,∠B= , ∠C= .
40°
60°
80°
A
B
C
D
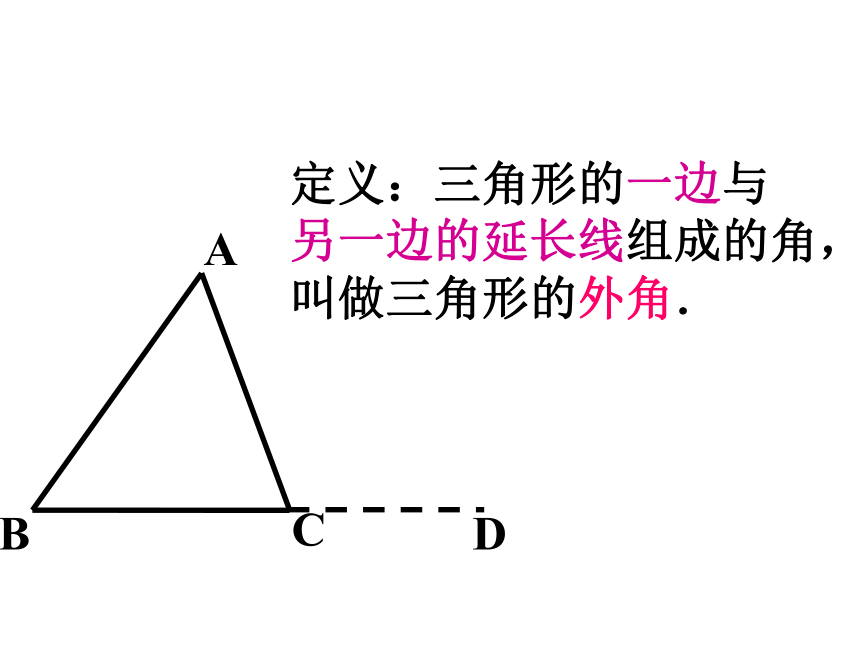
定义:三角形的一边与
另一边的延长线组成的角,叫做三角形的外角.
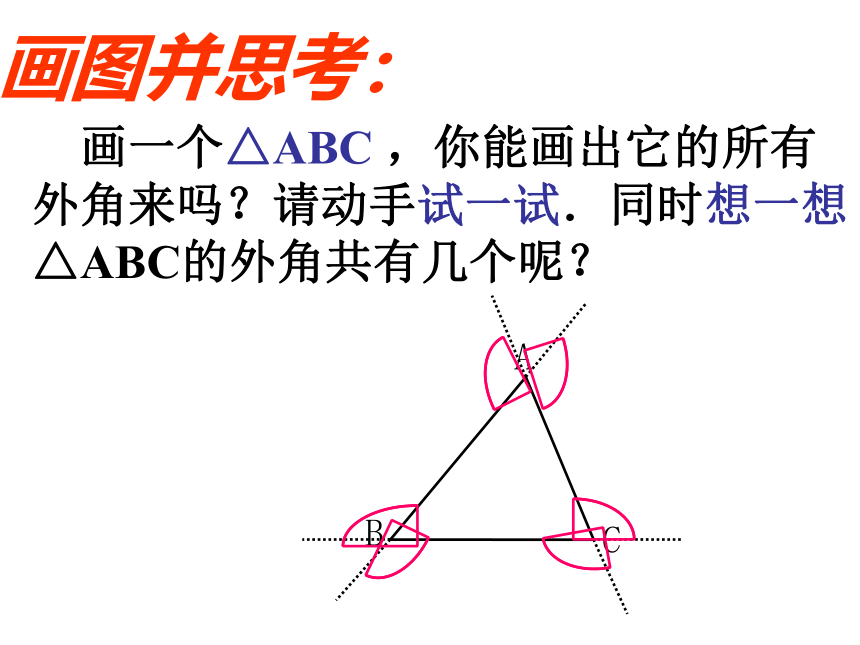
画图并思考:
画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
A
B
C
归纳:
每一个三角形都有6个外角.
每一个顶点处的外角都有2个,这两个外角是对顶角.
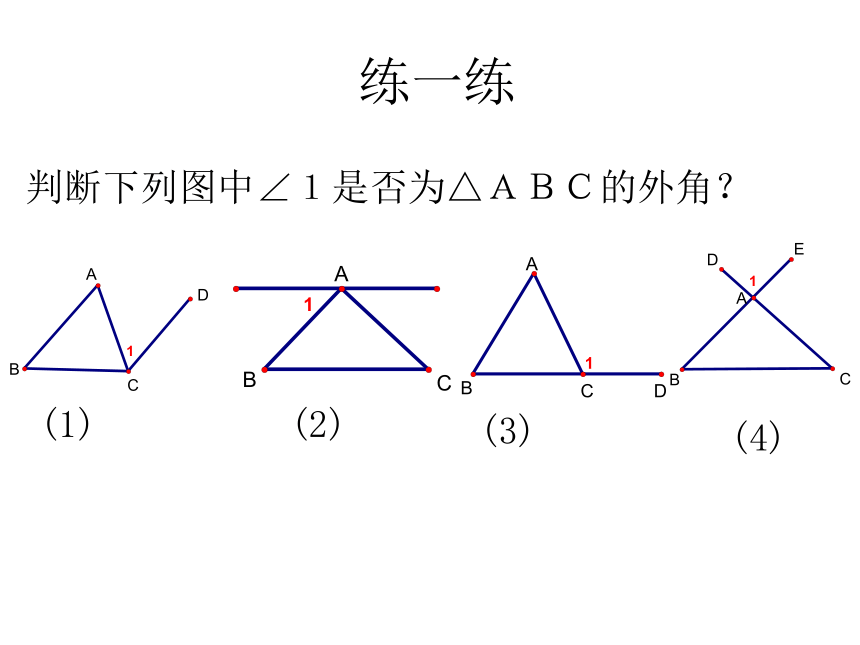
(1)
(2)
(3)
判断下列图中∠1是否为△ABC的外角?
(4)
练一练
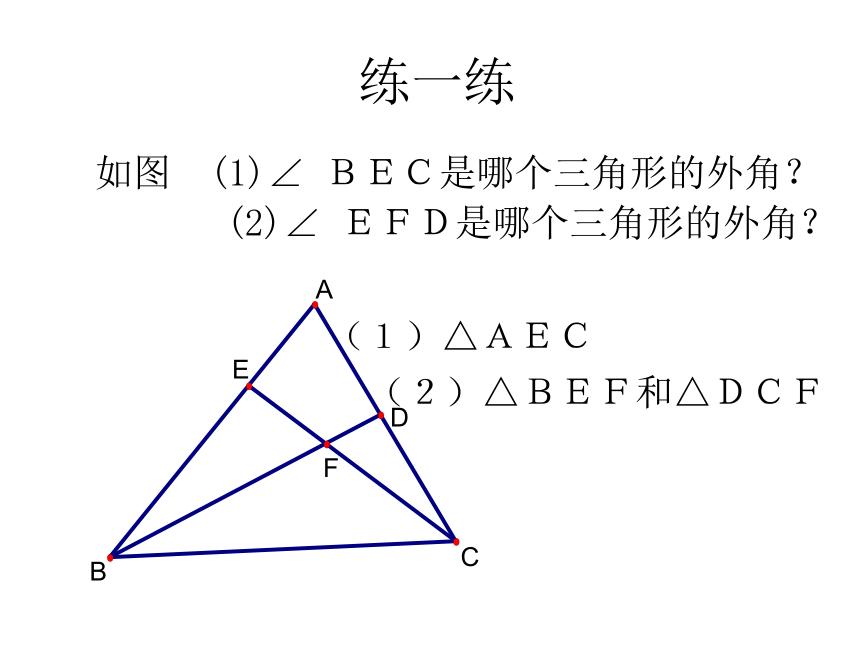
如图 (1)∠ BEC是哪个三角形的外角?
(1)△AEC
(2)△BEF和△DCF
(2)∠ EFD是哪个三角形的外角?
练一练
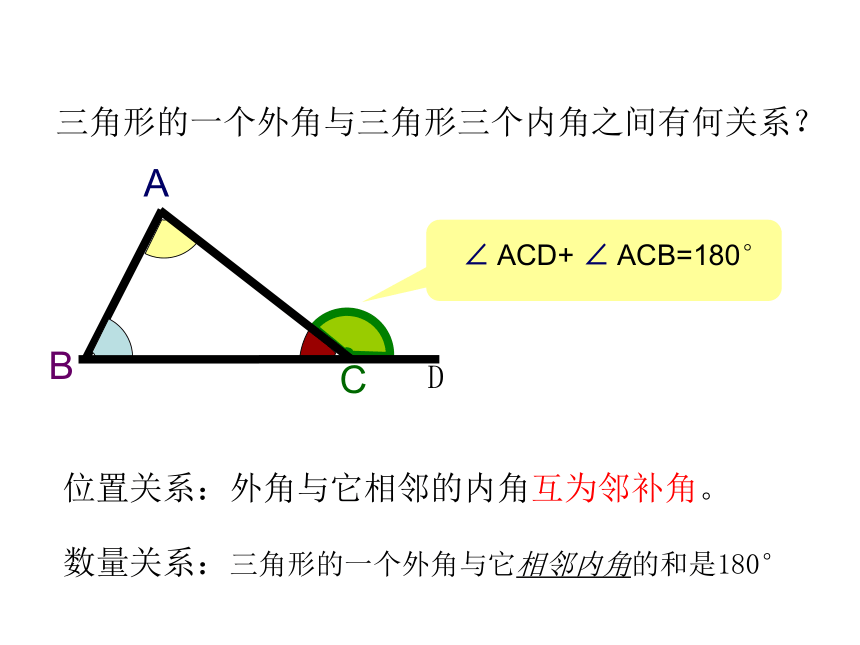
三角形的一个外角与三角形三个内角之间有何关系?
A
B
C
D
∠ ACD+ ∠ ACB=180°
数量关系:三角形的一个外角与它相邻内角的和是180°
位置关系:外角与它相邻的内角互为邻补角。
三角形的一个外角与它不相邻的两 个内角之间有何关系?
A
B
C
D
三角形的一个外角等于与它不相邻的两个内角的和。
∠ ACD+ ∠ ACB=180°
∠ACD= ∠ A+ ∠ B
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
三角形的一个外角等于与它不相邻的两个内角的和。
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
三角形的一个外角等于与它不相邻的两个内角的和。
D
∠ACD+ ∠ACB=180°
∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
三角形的一个外角等于与它不相邻的两个内角的和。
A
C
B
D
∵∠ACD 是△ABC的一个外角,
∴∠ACD= ∠B+ ∠A
2、三角形的一个外角等于与它不相邻的两个内角的和;
1、三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系:
1、说出下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=90°
∠1=95°
∠1=85°
60°
60°
20°
∠1=80°, ∠2=40°
巩固练习
例题讲解
3
2
1
A
B
C
5
6
4
结论:三角形的外角和等于360°
∵∠1+∠4=180°,
∠2+∠5=180°,
∠3+∠6=180°
∴∠1+∠4+∠2+∠5+∠3+∠6=540°
∵∠4+∠5+∠6=180°
∴∠1+∠2+∠3=360°
2
如图,在△ABC的每个顶点处各取一个外角∠1、∠2 、∠3 ,你能求出∠1+∠2 +∠3 的度数吗?
练一练
1、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
练一练
1
2
3
A
D
E
C
F
B
N
P
M
2、如图,∠A+∠B+∠B+∠D+∠E+∠F的度数.
∵∠A+∠B=∠1,∠C+∠D=∠2,∠E+∠F=∠3
∴∠A+∠B+∠C+∠D+
∠E+∠F=∠1+∠2+∠3
∵∠1+∠2+∠3=360°
∴∠A+∠B+∠C+∠D+
∠E+∠F= 360°
课堂小结
2、三角形的一个外角等于与它不相邻的两个内角的和;
1、三角形的一个外角与它相邻的内角互补;
(二)三角形的外角与内角的关系:
(三) 三角形的外角和为360°。
(一)三角形的外角的定义:三角形的一边与 另一边的延长线组成的角.
作 业
这节课我们学习到这里,再见!
1.三角形的内角和定理的内容
2、在ABC中,
(1)若∠C=90°,∠A=30 ° ,则∠B= ;
65°
60°
(2)若∠A=50 ° ,∠B=∠C,则∠B= .
旧知回顾
3、在△ABC中,
若∠A:∠B:∠C=2:3:4,则∠A= ,∠B= , ∠C= .
40°
60°
80°
A
B
C
D
定义:三角形的一边与
另一边的延长线组成的角,叫做三角形的外角.
画图并思考:
画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
A
B
C
归纳:
每一个三角形都有6个外角.
每一个顶点处的外角都有2个,这两个外角是对顶角.
(1)
(2)
(3)
判断下列图中∠1是否为△ABC的外角?
(4)
练一练
如图 (1)∠ BEC是哪个三角形的外角?
(1)△AEC
(2)△BEF和△DCF
(2)∠ EFD是哪个三角形的外角?
练一练
三角形的一个外角与三角形三个内角之间有何关系?
A
B
C
D
∠ ACD+ ∠ ACB=180°
数量关系:三角形的一个外角与它相邻内角的和是180°
位置关系:外角与它相邻的内角互为邻补角。
三角形的一个外角与它不相邻的两 个内角之间有何关系?
A
B
C
D
三角形的一个外角等于与它不相邻的两个内角的和。
∠ ACD+ ∠ ACB=180°
∠ACD= ∠ A+ ∠ B
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
三角形的一个外角等于与它不相邻的两个内角的和。
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
三角形的一个外角等于与它不相邻的两个内角的和。
D
∠ACD+ ∠ACB=180°
∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
三角形的一个外角等于与它不相邻的两个内角的和。
A
C
B
D
∵∠ACD 是△ABC的一个外角,
∴∠ACD= ∠B+ ∠A
2、三角形的一个外角等于与它不相邻的两个内角的和;
1、三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系:
1、说出下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=90°
∠1=95°
∠1=85°
60°
60°
20°
∠1=80°, ∠2=40°
巩固练习
例题讲解
3
2
1
A
B
C
5
6
4
结论:三角形的外角和等于360°
∵∠1+∠4=180°,
∠2+∠5=180°,
∠3+∠6=180°
∴∠1+∠4+∠2+∠5+∠3+∠6=540°
∵∠4+∠5+∠6=180°
∴∠1+∠2+∠3=360°
2
如图,在△ABC的每个顶点处各取一个外角∠1、∠2 、∠3 ,你能求出∠1+∠2 +∠3 的度数吗?
练一练
1、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
练一练
1
2
3
A
D
E
C
F
B
N
P
M
2、如图,∠A+∠B+∠B+∠D+∠E+∠F的度数.
∵∠A+∠B=∠1,∠C+∠D=∠2,∠E+∠F=∠3
∴∠A+∠B+∠C+∠D+
∠E+∠F=∠1+∠2+∠3
∵∠1+∠2+∠3=360°
∴∠A+∠B+∠C+∠D+
∠E+∠F= 360°
课堂小结
2、三角形的一个外角等于与它不相邻的两个内角的和;
1、三角形的一个外角与它相邻的内角互补;
(二)三角形的外角与内角的关系:
(三) 三角形的外角和为360°。
(一)三角形的外角的定义:三角形的一边与 另一边的延长线组成的角.
作 业
这节课我们学习到这里,再见!
