2020-2021学年人教版数学八年级上册11.2.2三角形的外角教学课件PPT(共20张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.2.2三角形的外角教学课件PPT(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览





文档简介
11.2
与三角形有关的角
11.2.2
三角形的外角
第十一章
三角形
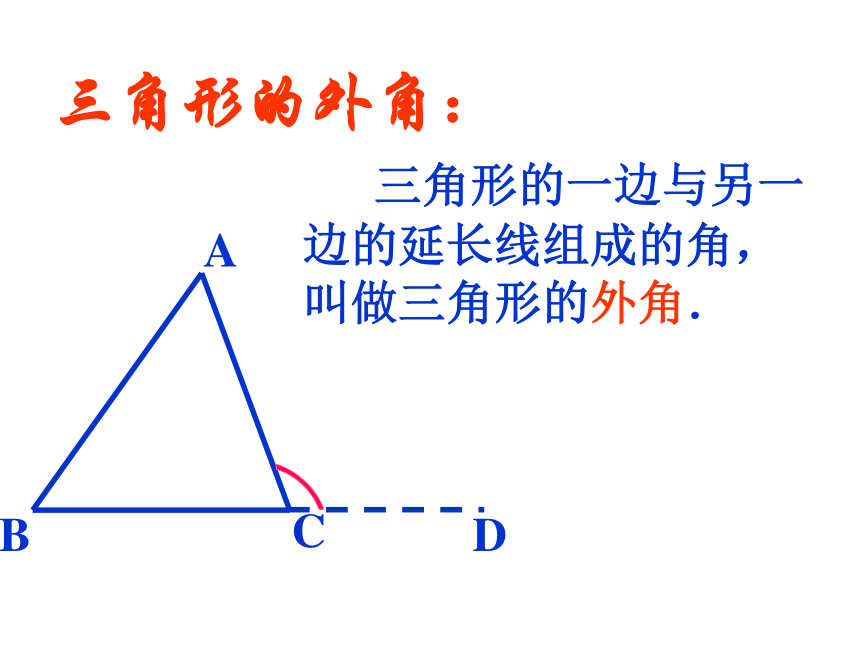
A
B
C
D
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
画图并思考:
画一个△ABC
,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳:
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个.
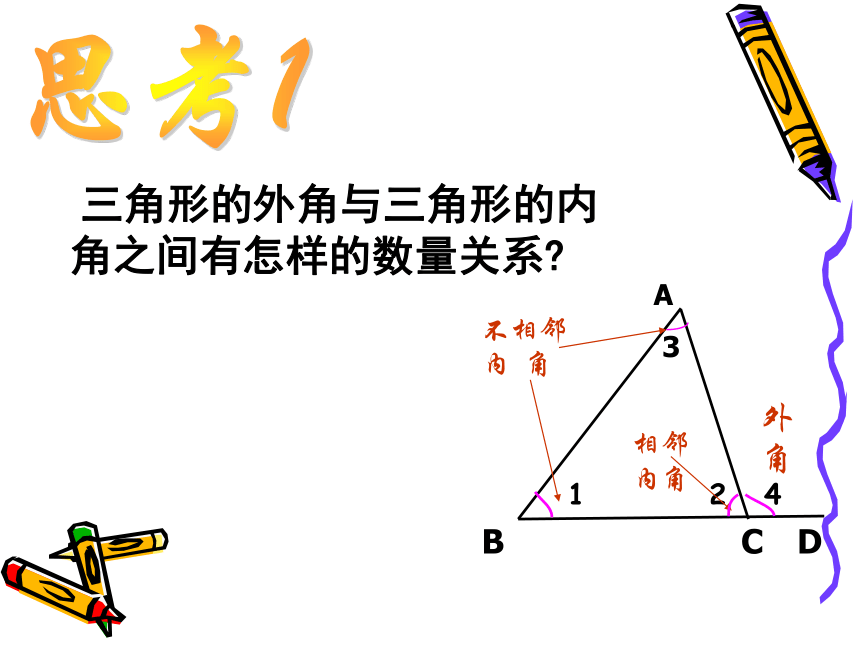
1
2
4
三角形的外角与三角形的内角之间有怎样的数量关系?
外角
A
3
B
C
D
相邻内角
不相邻
内
角
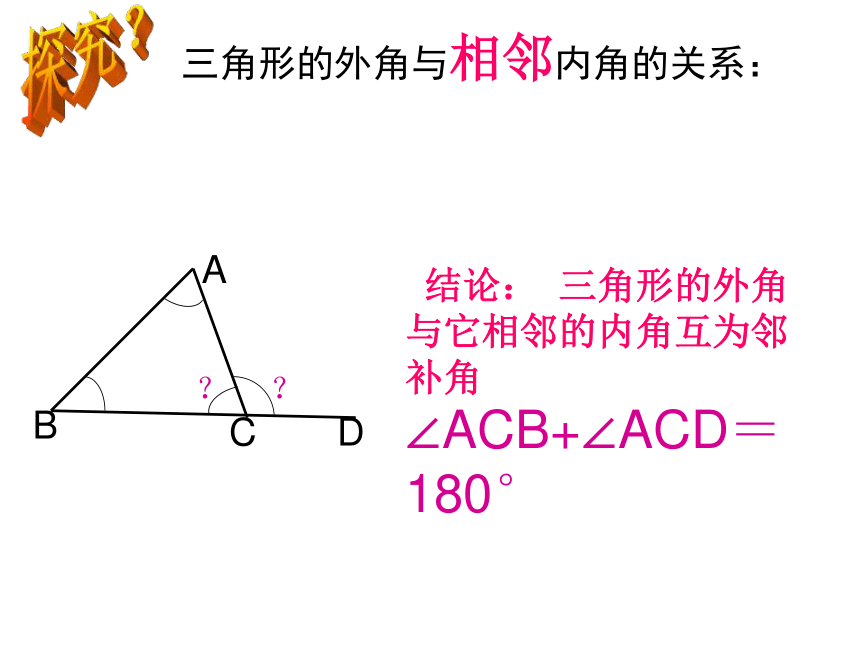
三角形的外角与相邻内角的关系:
A
B
C
D
?
?
结论:
三角形的外角与它相邻的内角互为邻补角∠ACB+∠ACD=180°
A
C
B
D
2、如图,
∠ACD
是△ABC的一个外角,试说明∠ACD=
∠B+
∠A
你能说出三角形的外角与每一个不相邻的内角之间的关系吗?
A
B
C
D
证明:
△ABC中
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
∠ACB+∠ACD=180°(平角定义)
∴∠ACD=∠A+∠B(等量代换)
证明外角定理:∠ACD=
∠
A+
∠
B
D
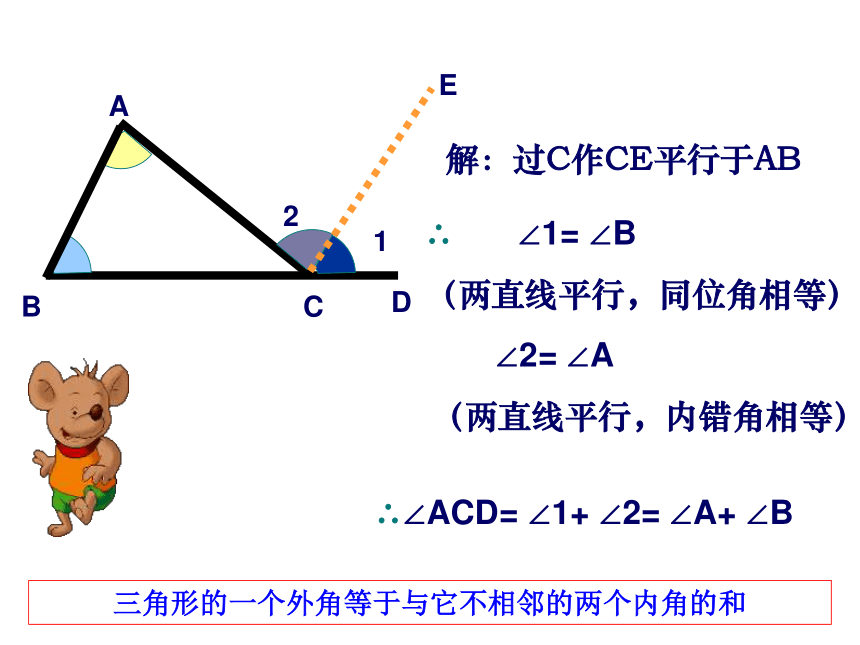
解:过C作CE平行于AB
A
B
C
1
2
∴
∠1=
∠B
(两直线平行,同位角相等)
∠2=
∠A
(两直线平行,内错角相等)
∴∠ACD=
∠1+
∠2=
∠A+
∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
3、三角形的一个外角大于任何一个与它不相邻的内角。
2、三角形的一个外角等于与它不相邻的两个内角的和;
1、三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系:
1
60°
110°
练一练:
1、求下列各图中∠1的度数。
50°
45°
1
35°
120°
1
练一练:2、把图中∠1、
∠2、
∠3按从大到小的顺序排列,并说明理由。
解:∠1>
∠2>
∠3
3
2
1
A
B
C
D
E
3
2
1
A
B
C
5
6
4
思考
已知:如图,∠1、∠2、∠3是△ABC的三个外角
求证:∠1+∠2+∠3=360°
结论:三角形的外角和等于360°
通常把一个三角形每一个顶点处的一个外角的和叫做三角形的外角和。
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
解:过A作AD平行于BC
∠3=
∠4
B
C
1
2
3
4
A
∠2=
∠BAD
∴
∠1+
∠2+
∠3
=
∠1+
∠4+
∠BAD=360°
两直线平行,同位角相等
D
∠2+
∠
3=
∠
4+∠BAD
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的一个外角等于两个内角的和。(
)
3、三角形的一个外角大于任何一个内角。(
)
4、三角形的一个内角小于任何一个与它不相邻的外角。(
)
探究2
如图,∠A=50°,∠B=40°,∠C=30°,求∠BPC的度数。
如图,△ABE
和△ADC是△ABC
分别沿着
AB、AC
边翻折180°形成的.
若∠1:∠2:∠3=13:3:2,
则∠α的度数为
.
巩固练习
a
3
2
1
D
E
A
B
C
a
3
2
1
D
E
A
B
C
1
2
3
B
A
C
P
N
M
D
E
F
∠A+∠B+∠C+∠D+∠E+∠F=____。
360°
A
B
C
D
E
(1)若∠C=30°,求∠A+
∠B+
∠D+
∠E的值
1
三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角。
2
三角形的外角和等于360
?
3
在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
与三角形有关的角
11.2.2
三角形的外角
第十一章
三角形
A
B
C
D
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
画图并思考:
画一个△ABC
,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳:
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个.
1
2
4
三角形的外角与三角形的内角之间有怎样的数量关系?
外角
A
3
B
C
D
相邻内角
不相邻
内
角
三角形的外角与相邻内角的关系:
A
B
C
D
?
?
结论:
三角形的外角与它相邻的内角互为邻补角∠ACB+∠ACD=180°
A
C
B
D
2、如图,
∠ACD
是△ABC的一个外角,试说明∠ACD=
∠B+
∠A
你能说出三角形的外角与每一个不相邻的内角之间的关系吗?
A
B
C
D
证明:
△ABC中
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
∠ACB+∠ACD=180°(平角定义)
∴∠ACD=∠A+∠B(等量代换)
证明外角定理:∠ACD=
∠
A+
∠
B
D
解:过C作CE平行于AB
A
B
C
1
2
∴
∠1=
∠B
(两直线平行,同位角相等)
∠2=
∠A
(两直线平行,内错角相等)
∴∠ACD=
∠1+
∠2=
∠A+
∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
3、三角形的一个外角大于任何一个与它不相邻的内角。
2、三角形的一个外角等于与它不相邻的两个内角的和;
1、三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系:
1
60°
110°
练一练:
1、求下列各图中∠1的度数。
50°
45°
1
35°
120°
1
练一练:2、把图中∠1、
∠2、
∠3按从大到小的顺序排列,并说明理由。
解:∠1>
∠2>
∠3
3
2
1
A
B
C
D
E
3
2
1
A
B
C
5
6
4
思考
已知:如图,∠1、∠2、∠3是△ABC的三个外角
求证:∠1+∠2+∠3=360°
结论:三角形的外角和等于360°
通常把一个三角形每一个顶点处的一个外角的和叫做三角形的外角和。
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
解:过A作AD平行于BC
∠3=
∠4
B
C
1
2
3
4
A
∠2=
∠BAD
∴
∠1+
∠2+
∠3
=
∠1+
∠4+
∠BAD=360°
两直线平行,同位角相等
D
∠2+
∠
3=
∠
4+∠BAD
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的一个外角等于两个内角的和。(
)
3、三角形的一个外角大于任何一个内角。(
)
4、三角形的一个内角小于任何一个与它不相邻的外角。(
)
探究2
如图,∠A=50°,∠B=40°,∠C=30°,求∠BPC的度数。
如图,△ABE
和△ADC是△ABC
分别沿着
AB、AC
边翻折180°形成的.
若∠1:∠2:∠3=13:3:2,
则∠α的度数为
.
巩固练习
a
3
2
1
D
E
A
B
C
a
3
2
1
D
E
A
B
C
1
2
3
B
A
C
P
N
M
D
E
F
∠A+∠B+∠C+∠D+∠E+∠F=____。
360°
A
B
C
D
E
(1)若∠C=30°,求∠A+
∠B+
∠D+
∠E的值
1
三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角。
2
三角形的外角和等于360
?
3
在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
