2020-2021学年人教版数学八年级上册11.2.2三角形的外角课件(共23张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.2.2三角形的外角课件(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览







文档简介
三角形的内角和
本课内容
本节内容
5.4
请同学们用量角器测量图5-27中△ABC的三个内角∠A,∠B,∠C,并分别得出三组数据,分别计算∠A+∠B+∠C的值并推测三角形的内角和应该等于多少.你能讲出道理吗?
动脑筋
图5-27
分析 为了说明∠A+∠B+∠C=180°的理由,我们
可以把三个内角移到同一个顶点(如图5-28).
于是,我们将∠B沿着直线BC平移,使B点和C点重合,则∠B就变成了∠1,CE平行于AB,因此∠A=∠2(两直线平行,内错角相等).
图5-28
又∠1+∠2+∠ACB=180°,
所以∠B+∠A+∠C=180°.
结论
三角形的内角和等于180°.
三个角都是锐角的三角形叫做锐角三角形.
有一个角是直角的三角形叫做直角三角形.
有一个角是钝角的三角形叫做钝角三角形.
锐角三角形和钝角三角形合称斜三角形.
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC”.
在直角三角形中,夹直角的两边叫做直角边,直角的对边叫做斜边.
两边相等的三角形叫做等腰三角形,两条直角边相等的直角三角形叫做等腰直角三角形.
由三角形内角和性质,容易得出下面的结论:
结论
直角三角形的两个锐角互为余角.
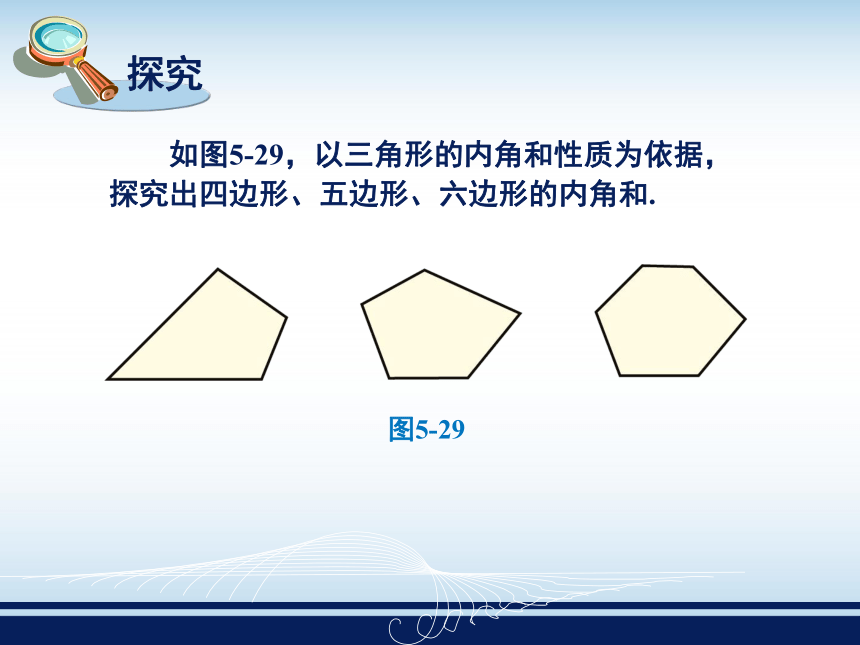
如图5-29,以三角形的内角和性质为依据,探究出四边形、五边形、六边形的内角和.
探究
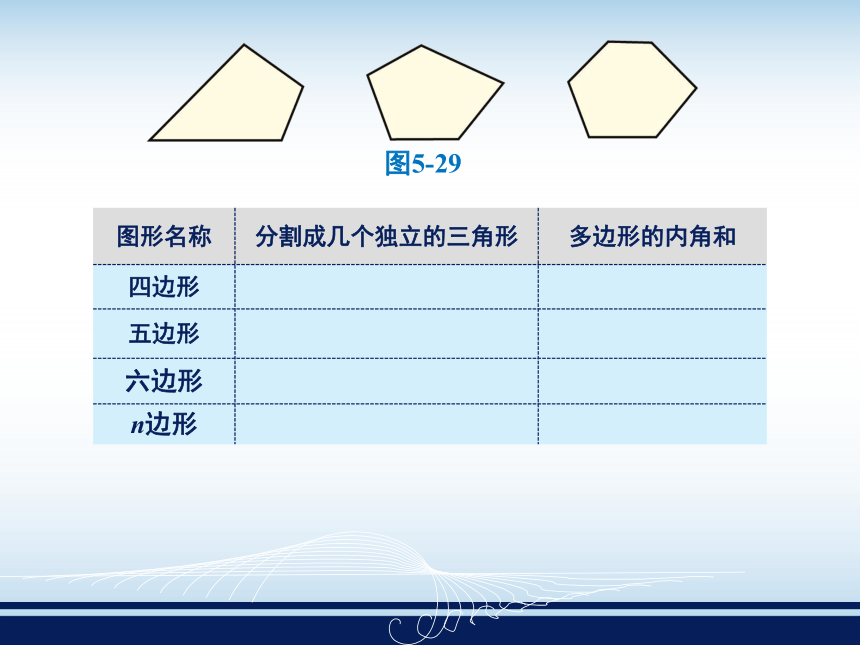
图5-29
图形名称
分割成几个独立的三角形
多边形的内角和
四边形
五边形
六边形
n边形
图5-29
练习
1. 填空:
(1)在△ABC中,∠A=90°,C=30°,
则∠B= ;
(2)在△ABC中,∠A=60°,∠B=∠C,
则∠B= ;
(3)在△ABC中,∠A-∠B=50°,∠C-∠B=40°,
则∠B= .
60°
60°
30°
2. 如图5-30,已知Rt△ABC,∠ACB=90°,CD⊥AB,垂足是D.
(1)数一数图中有几个直角三角形,并说出它
们的直角边和斜边;
答:图中有三个
直角三角形.
图5-30
(2)∠1与∠2是 关系;
∠2与∠B是 关系;
∠A与∠2是 关系;
∠1与∠B是 关系.
图5-30
互余
互余
相等
相等
如图5-31,把△ABC的一边BC延长,得到∠ACD.
探究
像这样,三角形一边与另一边的延长线组成的角,叫做三角形的外角.
对外角∠ACD而言,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
三角形的外角与内角之间有什么样的关系呢?
你能讲出道理吗?
由三角形内角和等于180°.
可以得到下面的结论:
结论
三角形的一个外角大于任何一个和它不相邻的内角.
三角形的一个外角等于和它不相邻的两个内角的和.
动脑筋
与三角形的一个内角相邻的外角有多少个?它们之间有什么关系?
如图5-32,对于△ABC每一个内角取它的一个外角.如∠ACE,∠BAF,∠CBD,量一量这三个外角的大小,猜一猜任意三角形的三个外角的和是多少.
图5-32
分析 因为∠ACE =∠1+∠2,(为什么?)
图5-32
∠BAF =∠2+∠3,(为什么?)
∠CBD =∠1+∠3,(为什么?)
所以∠ACE+∠BAF+∠CBD
= 2(∠1+∠2+∠3)
= 2×180°
= 360°.
结论
三角形的三个外角和等于360°.
你还能用别的方法得出这一结论吗?
练习
1. 画出图5-33中△ABC所有的外角.
答:延长BA至D,延长CB至E,延长AC至F,
延长CA至M,延长BC至N,延长AB至P,
从而易观察得到有六个外角.
图5-33
D
E
F
M
N
P
2. 如图5-34,已知∠DAC=100°,∠ABC=30°, 求∠ACB的值.
答:∵∠30°+∠C=100°.
则∠C = 100°- 30°= 70°.
图34
结 束
本课内容
本节内容
5.4
请同学们用量角器测量图5-27中△ABC的三个内角∠A,∠B,∠C,并分别得出三组数据,分别计算∠A+∠B+∠C的值并推测三角形的内角和应该等于多少.你能讲出道理吗?
动脑筋
图5-27
分析 为了说明∠A+∠B+∠C=180°的理由,我们
可以把三个内角移到同一个顶点(如图5-28).
于是,我们将∠B沿着直线BC平移,使B点和C点重合,则∠B就变成了∠1,CE平行于AB,因此∠A=∠2(两直线平行,内错角相等).
图5-28
又∠1+∠2+∠ACB=180°,
所以∠B+∠A+∠C=180°.
结论
三角形的内角和等于180°.
三个角都是锐角的三角形叫做锐角三角形.
有一个角是直角的三角形叫做直角三角形.
有一个角是钝角的三角形叫做钝角三角形.
锐角三角形和钝角三角形合称斜三角形.
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC”.
在直角三角形中,夹直角的两边叫做直角边,直角的对边叫做斜边.
两边相等的三角形叫做等腰三角形,两条直角边相等的直角三角形叫做等腰直角三角形.
由三角形内角和性质,容易得出下面的结论:
结论
直角三角形的两个锐角互为余角.
如图5-29,以三角形的内角和性质为依据,探究出四边形、五边形、六边形的内角和.
探究
图5-29
图形名称
分割成几个独立的三角形
多边形的内角和
四边形
五边形
六边形
n边形
图5-29
练习
1. 填空:
(1)在△ABC中,∠A=90°,C=30°,
则∠B= ;
(2)在△ABC中,∠A=60°,∠B=∠C,
则∠B= ;
(3)在△ABC中,∠A-∠B=50°,∠C-∠B=40°,
则∠B= .
60°
60°
30°
2. 如图5-30,已知Rt△ABC,∠ACB=90°,CD⊥AB,垂足是D.
(1)数一数图中有几个直角三角形,并说出它
们的直角边和斜边;
答:图中有三个
直角三角形.
图5-30
(2)∠1与∠2是 关系;
∠2与∠B是 关系;
∠A与∠2是 关系;
∠1与∠B是 关系.
图5-30
互余
互余
相等
相等
如图5-31,把△ABC的一边BC延长,得到∠ACD.
探究
像这样,三角形一边与另一边的延长线组成的角,叫做三角形的外角.
对外角∠ACD而言,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
三角形的外角与内角之间有什么样的关系呢?
你能讲出道理吗?
由三角形内角和等于180°.
可以得到下面的结论:
结论
三角形的一个外角大于任何一个和它不相邻的内角.
三角形的一个外角等于和它不相邻的两个内角的和.
动脑筋
与三角形的一个内角相邻的外角有多少个?它们之间有什么关系?
如图5-32,对于△ABC每一个内角取它的一个外角.如∠ACE,∠BAF,∠CBD,量一量这三个外角的大小,猜一猜任意三角形的三个外角的和是多少.
图5-32
分析 因为∠ACE =∠1+∠2,(为什么?)
图5-32
∠BAF =∠2+∠3,(为什么?)
∠CBD =∠1+∠3,(为什么?)
所以∠ACE+∠BAF+∠CBD
= 2(∠1+∠2+∠3)
= 2×180°
= 360°.
结论
三角形的三个外角和等于360°.
你还能用别的方法得出这一结论吗?
练习
1. 画出图5-33中△ABC所有的外角.
答:延长BA至D,延长CB至E,延长AC至F,
延长CA至M,延长BC至N,延长AB至P,
从而易观察得到有六个外角.
图5-33
D
E
F
M
N
P
2. 如图5-34,已知∠DAC=100°,∠ABC=30°, 求∠ACB的值.
答:∵∠30°+∠C=100°.
则∠C = 100°- 30°= 70°.
图34
结 束
