2020-2021学年人教版数学八年级上册11.2与三角形有关的角复习课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.2与三角形有关的角复习课件(共15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 732.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览





文档简介
温故而知新
--《 论语 》
与三角形有关的角
-----复习课
辉南二中 刘晶
学习目标:
1.进一步理解掌握三角形的内角和定理、内外角关系定理及应用.
2.体会方程思想、整体思想等知识与方法,提高探究的能力及说理能力.
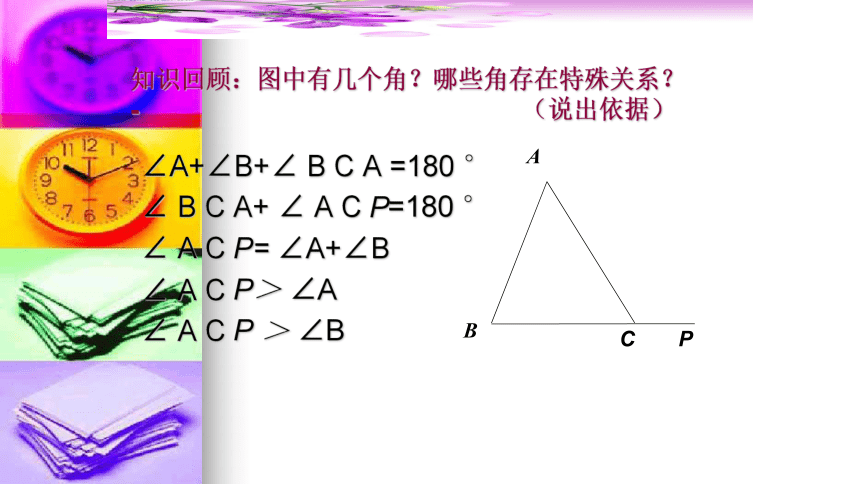
知识回顾:图中有几个角?哪些角存在特殊关系? - (说出依据)
∠A+∠B+∠ B C A =180 °
∠ B C A+ ∠ A C P=180 °
∠ A C P= ∠A+∠B
∠ A C P> ∠A
∠ A C P > ∠B
A
B
C
P
1、共四关,每关设置一道题;
2、准备练习本,分别标上序号1、2、3、4;
3、在规定时间内独立答题,完成后交予同桌;
4、每位同学是运动员,同时是同桌的裁判员。
闯关说明
智勇大闯关
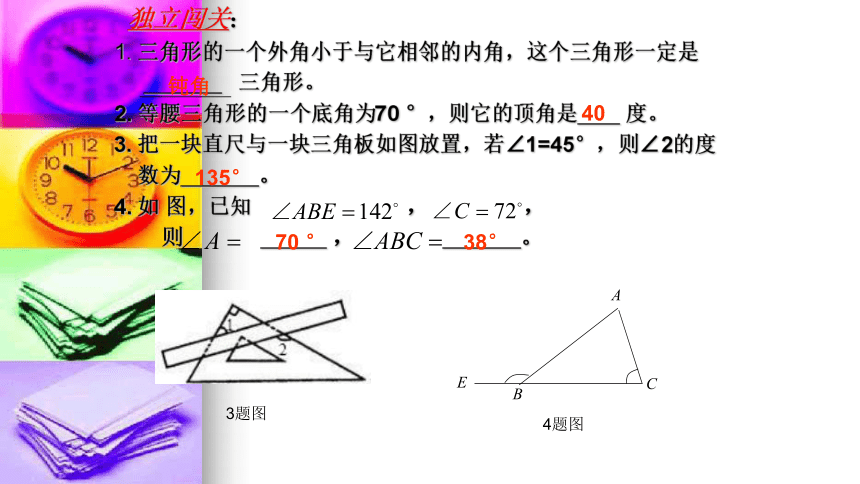
独立闯关:
1. 三角形的一个外角小于与它相邻的内角,这个三角形一定是
三角形。
2. 等腰三角形的一个底角为70 °,则它的顶角是 度。
3. 把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度
数为 。
4. 如 图,已知 , ,
则 , 。
A
B
C
E
3题图
4题图
钝角
40
135°
70 °
38°
能力提升、方法总结
探究一:已知△ABC中,
(1)∠A=20°,∠B-∠C=40°,则∠B=____°
(2)∠A:∠B:∠C=1:3:5,则∠B=_____°
思考:如何解决这类问题?
思想方法一(方程思想):在角的求值问题中,常利用图形关系或内角、外角之间关系进行转化,通过内角和或外角列方程来解决
应用训练: 已知△ABC中,∠ C = ∠B+20°, ∠B = 20°+∠A , 求∠A 的度数。
100
60
探究二:“8”字型
如图所示的“ ” 字型, ∠1、∠2、∠3、∠4存在什么关系?
存在着一个等式:
∠1+∠2=∠3+∠4
应用举例:
已知:如图
求∠A+∠B+∠C+∠D+∠E的度数。
思想方法二: (整体思想)从问题整体出发,把某些式子或者图形看成一个整体,把握他们的联系进行整体处理
M
N
能力比拼: 在下列图形中,上题结论 ∠A+∠B+∠C+∠D+∠E=180°是否成立?简述理由
(1)
(2)
(3)
探究三:下图中是否存在着如下等式 ∠D=∠A+∠B+∠C ?你能说明理由吗?(小组合作完成)
思想方法三:不规则图形可利用割 或补 的方法是
其转化成所学的图形,应用所学图形知识解决问题。
若AB∥CD,试探索各图形中∠BED与∠B、∠D的数量关系。
①
F
F
F
①方法1
①方法2
①方法3
②
③
④
F
F
F
F
F
②方法1
②方法2
②方法3
③标字母
④标字母
应用训练:
我的感悟我的收获
1、知识方面(温故)…
2、数学思想、方法(知新)…
作业:
必做作业:数学书80页,
练习 1, 2题。
选做作业
(1)如图 (1),在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC,
则∠EAD与∠B, ∠C有和数量关系?
(2)如图 (2),AE平分∠BAC,F为其上一点,FD⊥BC于D,这时∠EFD 与∠B、∠C又有何数量关系?
(3) 如图 (3),AE平分∠BAC,F为AE的延长线上的一点,FD⊥BC于D, 这时∠AFD与∠B、∠C又有何数量关系?
A
B
E
D
C
(1)
图7-2-2
A
B
E
G
C
F
A
B
E
G
C
(2)
F
D
D
(3)
给我最大快乐的,
不是已懂的知识,
而是不断的学习。
—— 高 斯
--《 论语 》
与三角形有关的角
-----复习课
辉南二中 刘晶
学习目标:
1.进一步理解掌握三角形的内角和定理、内外角关系定理及应用.
2.体会方程思想、整体思想等知识与方法,提高探究的能力及说理能力.
知识回顾:图中有几个角?哪些角存在特殊关系? - (说出依据)
∠A+∠B+∠ B C A =180 °
∠ B C A+ ∠ A C P=180 °
∠ A C P= ∠A+∠B
∠ A C P> ∠A
∠ A C P > ∠B
A
B
C
P
1、共四关,每关设置一道题;
2、准备练习本,分别标上序号1、2、3、4;
3、在规定时间内独立答题,完成后交予同桌;
4、每位同学是运动员,同时是同桌的裁判员。
闯关说明
智勇大闯关
独立闯关:
1. 三角形的一个外角小于与它相邻的内角,这个三角形一定是
三角形。
2. 等腰三角形的一个底角为70 °,则它的顶角是 度。
3. 把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度
数为 。
4. 如 图,已知 , ,
则 , 。
A
B
C
E
3题图
4题图
钝角
40
135°
70 °
38°
能力提升、方法总结
探究一:已知△ABC中,
(1)∠A=20°,∠B-∠C=40°,则∠B=____°
(2)∠A:∠B:∠C=1:3:5,则∠B=_____°
思考:如何解决这类问题?
思想方法一(方程思想):在角的求值问题中,常利用图形关系或内角、外角之间关系进行转化,通过内角和或外角列方程来解决
应用训练: 已知△ABC中,∠ C = ∠B+20°, ∠B = 20°+∠A , 求∠A 的度数。
100
60
探究二:“8”字型
如图所示的“ ” 字型, ∠1、∠2、∠3、∠4存在什么关系?
存在着一个等式:
∠1+∠2=∠3+∠4
应用举例:
已知:如图
求∠A+∠B+∠C+∠D+∠E的度数。
思想方法二: (整体思想)从问题整体出发,把某些式子或者图形看成一个整体,把握他们的联系进行整体处理
M
N
能力比拼: 在下列图形中,上题结论 ∠A+∠B+∠C+∠D+∠E=180°是否成立?简述理由
(1)
(2)
(3)
探究三:下图中是否存在着如下等式 ∠D=∠A+∠B+∠C ?你能说明理由吗?(小组合作完成)
思想方法三:不规则图形可利用割 或补 的方法是
其转化成所学的图形,应用所学图形知识解决问题。
若AB∥CD,试探索各图形中∠BED与∠B、∠D的数量关系。
①
F
F
F
①方法1
①方法2
①方法3
②
③
④
F
F
F
F
F
②方法1
②方法2
②方法3
③标字母
④标字母
应用训练:
我的感悟我的收获
1、知识方面(温故)…
2、数学思想、方法(知新)…
作业:
必做作业:数学书80页,
练习 1, 2题。
选做作业
(1)如图 (1),在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC,
则∠EAD与∠B, ∠C有和数量关系?
(2)如图 (2),AE平分∠BAC,F为其上一点,FD⊥BC于D,这时∠EFD 与∠B、∠C又有何数量关系?
(3) 如图 (3),AE平分∠BAC,F为AE的延长线上的一点,FD⊥BC于D, 这时∠AFD与∠B、∠C又有何数量关系?
A
B
E
D
C
(1)
图7-2-2
A
B
E
G
C
F
A
B
E
G
C
(2)
F
D
D
(3)
给我最大快乐的,
不是已懂的知识,
而是不断的学习。
—— 高 斯
