2020-2021学年人教版数学八年级上册11.2与三角形有关的角课件(第3课时)(共18张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.2与三角形有关的角课件(第3课时)(共18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览




文档简介
八年级
上册
11.2
与三角形有关的角
(第3课时)
课件说明
本节课内容是从三角形的内角的概念迁移到三角形
的外角的概念,进而研究三角形的外角的性质,再
通过例题进行巩固运用.
课件来源于jiaoxue5u.
课件说明
学习目标:
1.理解三角形的外角的概念.
2.掌握三角形的一个外角等于与它不相邻的两个内
角的和.
学习重点:
掌握三角形的一个外角等于与它不相邻的两个内角
的和.
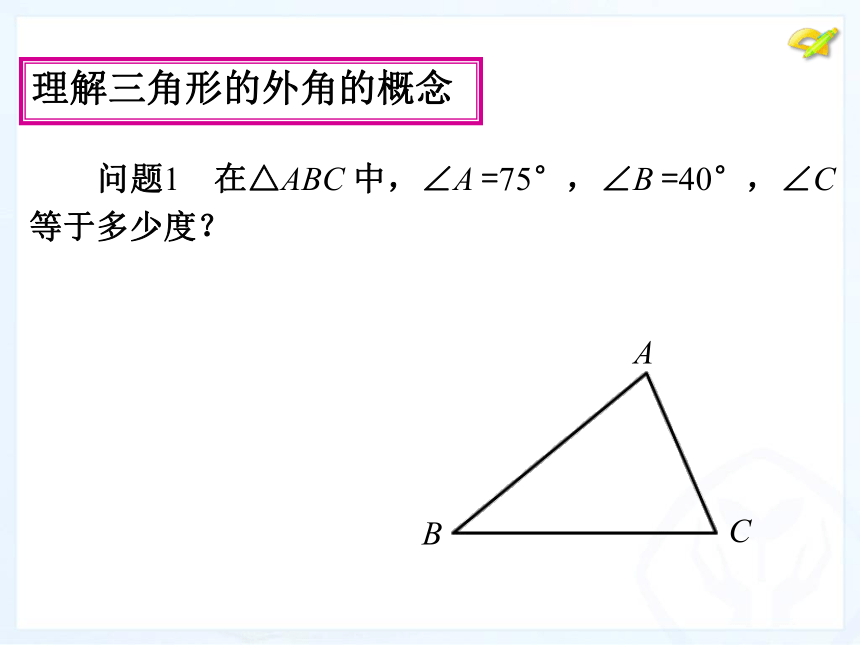
理解三角形的外角的概念
问题1
在△ABC
中,∠A
=75°,∠B
=40°,∠C
等于多少度?
A
B
C
课件来源于jiaoxue5u.
理解三角形的外角的概念
问题2
如图,把△ABC
的一边BC
延长,得到
∠ACD.这个角还是三角形的内角吗?
概念:
三角形的一边与另一边的
延长线组成的角,叫做三角形
的外角.
A
B
C
D
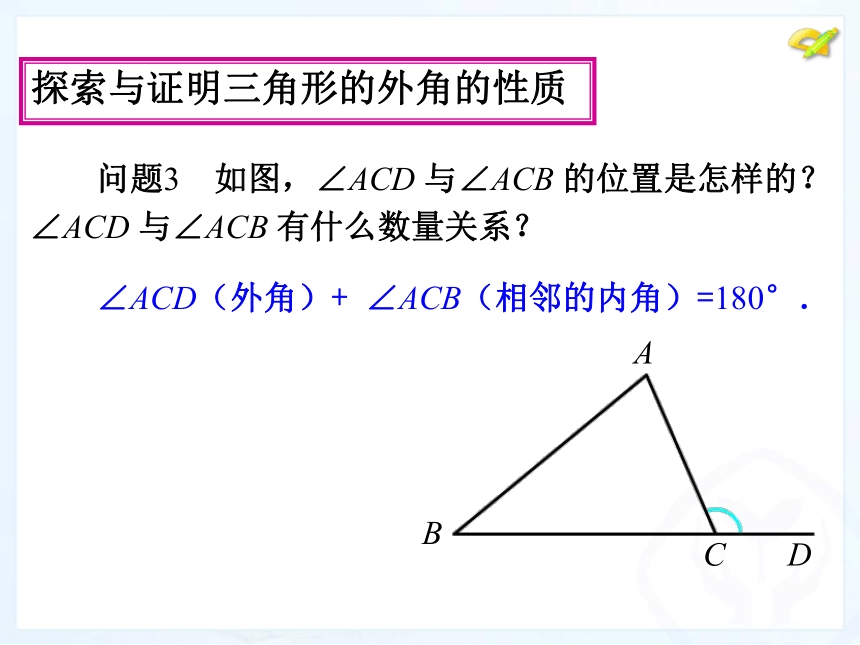
探索与证明三角形的外角的性质
∠ACD(外角)+
∠ACB(相邻的内角)=180°.
A
B
C
D
问题3
如图,∠ACD
与∠ACB
的位置是怎样的?
∠ACD
与∠ACB
有什么数量关系?
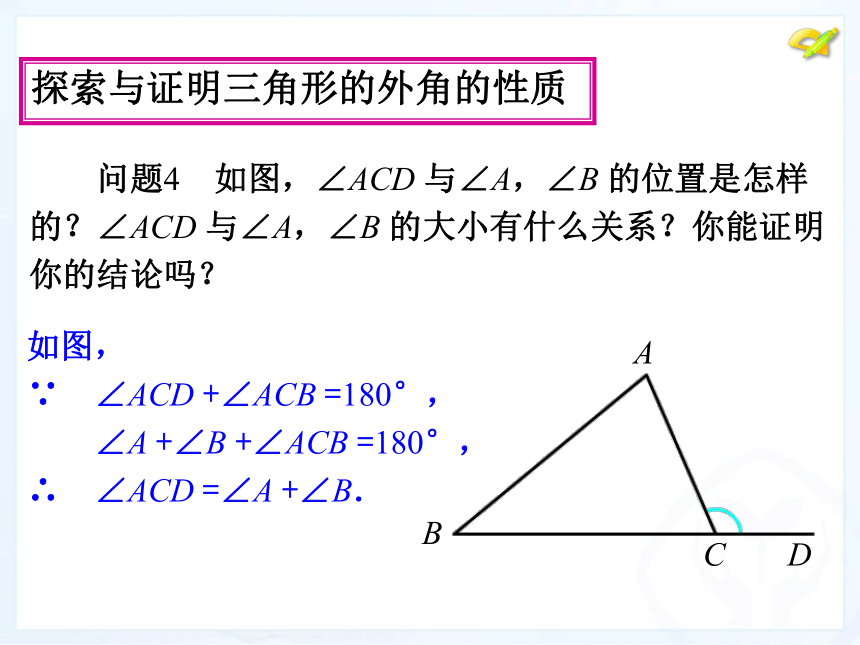
探索与证明三角形的外角的性质
如图,
∵ ∠ACD
+∠ACB
=180°,
∠A
+∠B
+∠ACB
=180°,
∴ ∠ACD
=∠A
+∠B.
A
B
C
D
问题4
如图,∠ACD
与∠A,∠B
的位置是怎样
的?∠ACD
与∠A,∠B
的大小有什么关系?你能证明
你的结论吗?
探索与证明三角形的外角的性质
三角形内角和定理的推论:
三角形的一个外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论,和定理一样,推
论可以作为进一步推理的依据.
∠C
∠3
∠DAC
∠4
课堂练习
练习1
如图,口答:
(1)∠1
=
+
;
(2)∠2
=
+
.
B
A
C
D
1
2
3
4
课件来源于jiaoxue5u.
课堂练习
练习2
如图,说出图形中∠1
的度数.
图中∠1的度数依次为:90°,85°,
95°,45°.
(1)
(2)
(3)
(4)
30°
60°
1
35°
60°
1
45°
50°
1
30°
15°
1
课件来源于jiaoxue5u.
课堂练习
练习3
如图,说出图形中∠1
和∠2
的度数:
(1)
(2)
(3)
1
1
1
2
2
2
60°
80°
30°
40°
40°
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
解法一:
∵ ∠BAE
=∠2
+∠3,
∠CBF
=∠1
+∠3,
∠ACD
=∠1
+∠2,
∴ ∠BAE
+∠CBF
+∠ACD
=
(∠2
+∠3)+(∠1
+∠3)
+
(∠1
+∠2)
A
B
F
C
D
E
1
2
3
课件来源于jiaoxue5u.
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
A
B
F
C
D
E
1
2
3
解法一:
=
2(∠1
+∠2
+∠3).
∵ ∠1
+∠2
+∠3
=180°,
∴ ∠BAE
+∠CBF
+∠ACD
=
2×180°
=360°.
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
解法二:
由∠1
+∠BAE
=180°,
∠2
+∠CBF
=180°,
∠3
+∠ACD
=180°,
得∠1
+∠2
+∠3
+
∠BAE
+∠CBF
+∠ACD
=
540°.
A
B
F
C
D
E
1
2
3
课件来源于jiaoxue5u.
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
A
B
F
C
D
E
1
2
3
解法二:
由∠1
+
∠2
+
∠3
=180°,
得∠BAE
+
∠CBF
+
∠ACD
=
540°-
180°
=360°.
40?
40?
⌒
课堂练习
A
B
D
C
练习 如图,D是△ABC
的BC
边上一点,∠B
=
∠BAD,∠ADC
=80°,∠BAC
=70°.
求:(1)∠B
的度数;(2)∠C
的度数.
(1)本节课学习了哪些主要内容?
(2)怎样探索并证明“三角形的一个外角等于与它不
相邻的两个内角的和”?
(3)你用了哪几种方法解答例题?
课堂小结
布置作业
教科书习题11.2第6、8题.
上册
11.2
与三角形有关的角
(第3课时)
课件说明
本节课内容是从三角形的内角的概念迁移到三角形
的外角的概念,进而研究三角形的外角的性质,再
通过例题进行巩固运用.
课件来源于jiaoxue5u.
课件说明
学习目标:
1.理解三角形的外角的概念.
2.掌握三角形的一个外角等于与它不相邻的两个内
角的和.
学习重点:
掌握三角形的一个外角等于与它不相邻的两个内角
的和.
理解三角形的外角的概念
问题1
在△ABC
中,∠A
=75°,∠B
=40°,∠C
等于多少度?
A
B
C
课件来源于jiaoxue5u.
理解三角形的外角的概念
问题2
如图,把△ABC
的一边BC
延长,得到
∠ACD.这个角还是三角形的内角吗?
概念:
三角形的一边与另一边的
延长线组成的角,叫做三角形
的外角.
A
B
C
D
探索与证明三角形的外角的性质
∠ACD(外角)+
∠ACB(相邻的内角)=180°.
A
B
C
D
问题3
如图,∠ACD
与∠ACB
的位置是怎样的?
∠ACD
与∠ACB
有什么数量关系?
探索与证明三角形的外角的性质
如图,
∵ ∠ACD
+∠ACB
=180°,
∠A
+∠B
+∠ACB
=180°,
∴ ∠ACD
=∠A
+∠B.
A
B
C
D
问题4
如图,∠ACD
与∠A,∠B
的位置是怎样
的?∠ACD
与∠A,∠B
的大小有什么关系?你能证明
你的结论吗?
探索与证明三角形的外角的性质
三角形内角和定理的推论:
三角形的一个外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论,和定理一样,推
论可以作为进一步推理的依据.
∠C
∠3
∠DAC
∠4
课堂练习
练习1
如图,口答:
(1)∠1
=
+
;
(2)∠2
=
+
.
B
A
C
D
1
2
3
4
课件来源于jiaoxue5u.
课堂练习
练习2
如图,说出图形中∠1
的度数.
图中∠1的度数依次为:90°,85°,
95°,45°.
(1)
(2)
(3)
(4)
30°
60°
1
35°
60°
1
45°
50°
1
30°
15°
1
课件来源于jiaoxue5u.
课堂练习
练习3
如图,说出图形中∠1
和∠2
的度数:
(1)
(2)
(3)
1
1
1
2
2
2
60°
80°
30°
40°
40°
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
解法一:
∵ ∠BAE
=∠2
+∠3,
∠CBF
=∠1
+∠3,
∠ACD
=∠1
+∠2,
∴ ∠BAE
+∠CBF
+∠ACD
=
(∠2
+∠3)+(∠1
+∠3)
+
(∠1
+∠2)
A
B
F
C
D
E
1
2
3
课件来源于jiaoxue5u.
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
A
B
F
C
D
E
1
2
3
解法一:
=
2(∠1
+∠2
+∠3).
∵ ∠1
+∠2
+∠3
=180°,
∴ ∠BAE
+∠CBF
+∠ACD
=
2×180°
=360°.
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
解法二:
由∠1
+∠BAE
=180°,
∠2
+∠CBF
=180°,
∠3
+∠ACD
=180°,
得∠1
+∠2
+∠3
+
∠BAE
+∠CBF
+∠ACD
=
540°.
A
B
F
C
D
E
1
2
3
课件来源于jiaoxue5u.
运用三角形的外角的性质
例
如图,∠BAE,∠CBF,∠ACD
是△ABC
的
三个外角,它们的和是多少?
A
B
F
C
D
E
1
2
3
解法二:
由∠1
+
∠2
+
∠3
=180°,
得∠BAE
+
∠CBF
+
∠ACD
=
540°-
180°
=360°.
40?
40?
⌒
课堂练习
A
B
D
C
练习 如图,D是△ABC
的BC
边上一点,∠B
=
∠BAD,∠ADC
=80°,∠BAC
=70°.
求:(1)∠B
的度数;(2)∠C
的度数.
(1)本节课学习了哪些主要内容?
(2)怎样探索并证明“三角形的一个外角等于与它不
相邻的两个内角的和”?
(3)你用了哪几种方法解答例题?
课堂小结
布置作业
教科书习题11.2第6、8题.
