2020-2021学年人教版数学八年级上册11.3.2多边形的内角和(共17张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.3.2多边形的内角和(共17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 14:48:40 | ||
图片预览





文档简介
第十一章 三角形
11.3.2 多边形的内角和
学习目标
1、掌握多边形的内角和定理和运用.
2、经历多边形内角和的探究,感受转化和方程的思想.
3、灵活运用内角和定理进行计算
一、一史(泰森多边形)
泰森提出了一种根据离散分布的气象站的降雨量来计算平均降雨量的方法,即将所有相邻气象站连成三角形,作这些三角形各边的垂直平分线,于是每个气象站周围的若干垂直平分线便围成一个多边形。并称这个多边形为泰森多边形。
二、复习回顾
1、正五边形,有_________个内角;
2、一个正五边形的每个内角为108°,则它的内角和为_______;
3、一个正六多边形的内角和为720°,则它的每个角为______________
5
540°
120°
自学课本P2 1-22,完成填空(7分钟).
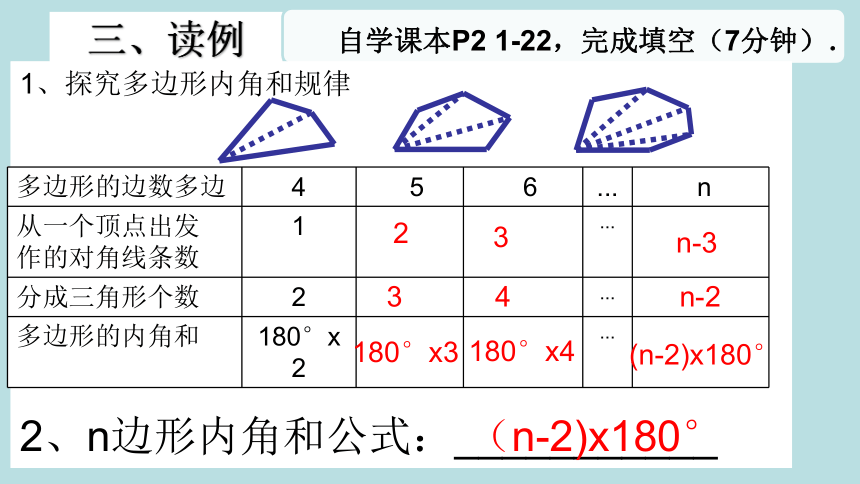
1、探究多边形内角和规律
2、n边形内角和公式:___________
多边形的边数多边
4
5
6
...
n
从一个顶点出发
作的对角线条数
1
...
分成三角形个数
2
...
多边形的内角和
180°x2
...
2
3
180°x3
3
180°x4
4
n-3
n-2
(n-2)x180°
(n-2)x180°
请问:把一个多边形分成几个三角形,还有其他分法?能得到多边形内角和公式?8分钟
(谁上台来,画一画,说一说)
思考
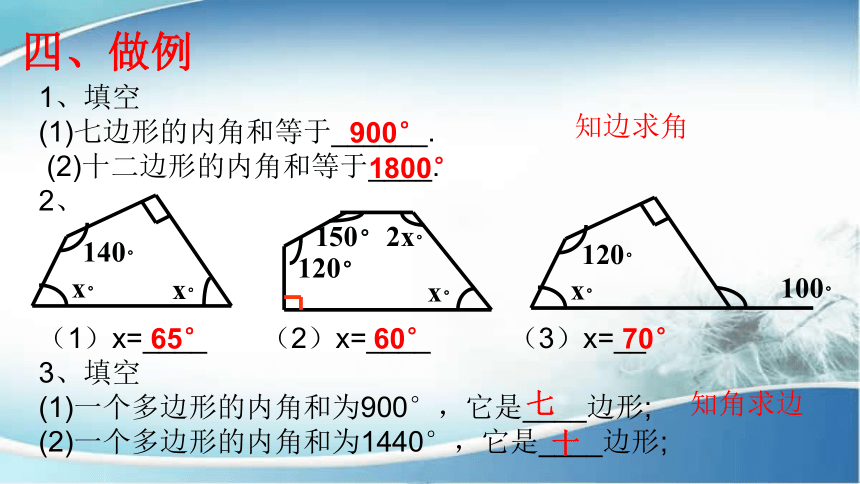
四、做例
1、填空
(1)七边形的内角和等于______.
(2)十二边形的内角和等于____.
2、
(1)x=____ (2)x=____ (3)x=__
3、填空
(1)一个多边形的内角和为900°,它是____边形;
(2)一个多边形的内角和为1440°,它是____边形;
x。
140。
x。
2x。
x。
120。
150。
x。
120。
100。
900°
1800°
十
65°
60°
70°
七
知边求角
知角求边
例:如果一个四边形的一组对角互补, 那么另一组对角有什么关系?
解:另一组角互补,理由如下:
如图所示,四边形ABCD中,∠A+∠C= 180°
∵∠A+∠B+ ∠C+ ∠D=(4-2)×180。=360°
∴∠B+∠D = 360° -(∠A+∠C )
= 360° - 180°
= 180°
这就是说,
如果四边形的一组对角互补,那么另一组对角也互补。
A
D
C
B
五、读例(课本例题学习)
六、做例(A组题)
1、二十二边形的内角和等于________;
2、一个多边形的内角和为1800°,它是_____边形;
3、一个多边形的各内角为120°,它是几边形 ?
3600°
十二
解:设它是n边形,得
120 n =(n-2) x180
解得 n=6
答:它是六边形
(3)强调:正多边形的每个内角=(n-2)x180°÷n
六、做例(B组题)
1、如图,在四边形ABCD中,∠A=∠C,∠B=∠D
AB与CD有怎样的位置关系?为什么?BC与AD呢?
A
B
D
C
解:AB∥CD,BC∥AD
理由如下:
∵∠A=∠C,∠B=∠D
∠A+∠C+∠B+∠D=360°
∴∠A+∠D=180°
∴ AB∥CD
∵∠A+∠B=180°
∴BC∥AD
六、做例(C组)
1、平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=____°.
24
1
2
3
提示:正多边形的每个内角=(n-2)x180°÷n
A
D
C
2
O
B
2、如图,四边形ADCD中,
的角平分线交于O点.求证
六、做例(C组题)
七、创例
请你做小老师,根据多边形内角和
新编一道题目。(同桌间交换做一下)
八、归纳小结
本节课我们学了哪些内容?
1.多边形的内角和(知边求和,知和求边).
2.会用内角和公式解决较复杂的问题几何.
4.重要数学思想方法(方程思想,转化思想)
九、堂上小测(5分钟)
1、八边形的内角和等于______.
2、一个多边形的内角和为1620°,它是_____边形
3、如图,在五边形ABCDE,∠A+∠B+∠E=300°,
DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A、60° B、65° C、55° D、50°
4、四边形的∠A、∠B、∠C、∠D的
内角之比为1:2:3:4,
那么∠B= ____
1080°
十一
A
B
E
D
C
P
A
72°
Thanks
For Your Attention
A
B
E
D
C
2
4
1
3
x
六、做例(C组题)
1、如图,五边形ABCDE的的内角都
相等,
求X得值。
解:
每个内角度数:(5-2)x180°÷5=108°
∵
∴
同理,
∵
∴
11.3.2 多边形的内角和
学习目标
1、掌握多边形的内角和定理和运用.
2、经历多边形内角和的探究,感受转化和方程的思想.
3、灵活运用内角和定理进行计算
一、一史(泰森多边形)
泰森提出了一种根据离散分布的气象站的降雨量来计算平均降雨量的方法,即将所有相邻气象站连成三角形,作这些三角形各边的垂直平分线,于是每个气象站周围的若干垂直平分线便围成一个多边形。并称这个多边形为泰森多边形。
二、复习回顾
1、正五边形,有_________个内角;
2、一个正五边形的每个内角为108°,则它的内角和为_______;
3、一个正六多边形的内角和为720°,则它的每个角为______________
5
540°
120°
自学课本P2 1-22,完成填空(7分钟).
1、探究多边形内角和规律
2、n边形内角和公式:___________
多边形的边数多边
4
5
6
...
n
从一个顶点出发
作的对角线条数
1
...
分成三角形个数
2
...
多边形的内角和
180°x2
...
2
3
180°x3
3
180°x4
4
n-3
n-2
(n-2)x180°
(n-2)x180°
请问:把一个多边形分成几个三角形,还有其他分法?能得到多边形内角和公式?8分钟
(谁上台来,画一画,说一说)
思考
四、做例
1、填空
(1)七边形的内角和等于______.
(2)十二边形的内角和等于____.
2、
(1)x=____ (2)x=____ (3)x=__
3、填空
(1)一个多边形的内角和为900°,它是____边形;
(2)一个多边形的内角和为1440°,它是____边形;
x。
140。
x。
2x。
x。
120。
150。
x。
120。
100。
900°
1800°
十
65°
60°
70°
七
知边求角
知角求边
例:如果一个四边形的一组对角互补, 那么另一组对角有什么关系?
解:另一组角互补,理由如下:
如图所示,四边形ABCD中,∠A+∠C= 180°
∵∠A+∠B+ ∠C+ ∠D=(4-2)×180。=360°
∴∠B+∠D = 360° -(∠A+∠C )
= 360° - 180°
= 180°
这就是说,
如果四边形的一组对角互补,那么另一组对角也互补。
A
D
C
B
五、读例(课本例题学习)
六、做例(A组题)
1、二十二边形的内角和等于________;
2、一个多边形的内角和为1800°,它是_____边形;
3、一个多边形的各内角为120°,它是几边形 ?
3600°
十二
解:设它是n边形,得
120 n =(n-2) x180
解得 n=6
答:它是六边形
(3)强调:正多边形的每个内角=(n-2)x180°÷n
六、做例(B组题)
1、如图,在四边形ABCD中,∠A=∠C,∠B=∠D
AB与CD有怎样的位置关系?为什么?BC与AD呢?
A
B
D
C
解:AB∥CD,BC∥AD
理由如下:
∵∠A=∠C,∠B=∠D
∠A+∠C+∠B+∠D=360°
∴∠A+∠D=180°
∴ AB∥CD
∵∠A+∠B=180°
∴BC∥AD
六、做例(C组)
1、平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=____°.
24
1
2
3
提示:正多边形的每个内角=(n-2)x180°÷n
A
D
C
2
O
B
2、如图,四边形ADCD中,
的角平分线交于O点.求证
六、做例(C组题)
七、创例
请你做小老师,根据多边形内角和
新编一道题目。(同桌间交换做一下)
八、归纳小结
本节课我们学了哪些内容?
1.多边形的内角和(知边求和,知和求边).
2.会用内角和公式解决较复杂的问题几何.
4.重要数学思想方法(方程思想,转化思想)
九、堂上小测(5分钟)
1、八边形的内角和等于______.
2、一个多边形的内角和为1620°,它是_____边形
3、如图,在五边形ABCDE,∠A+∠B+∠E=300°,
DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A、60° B、65° C、55° D、50°
4、四边形的∠A、∠B、∠C、∠D的
内角之比为1:2:3:4,
那么∠B= ____
1080°
十一
A
B
E
D
C
P
A
72°
Thanks
For Your Attention
A
B
E
D
C
2
4
1
3
x
六、做例(C组题)
1、如图,五边形ABCDE的的内角都
相等,
求X得值。
解:
每个内角度数:(5-2)x180°÷5=108°
∵
∴
同理,
∵
∴
