2020-2021学年人教版数学八年级上册11.3.2多边形的内角和(共23张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.3.2多边形的内角和(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 789.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览





文档简介
11.3.2 多边形的内角和
人教版八年级(上册)
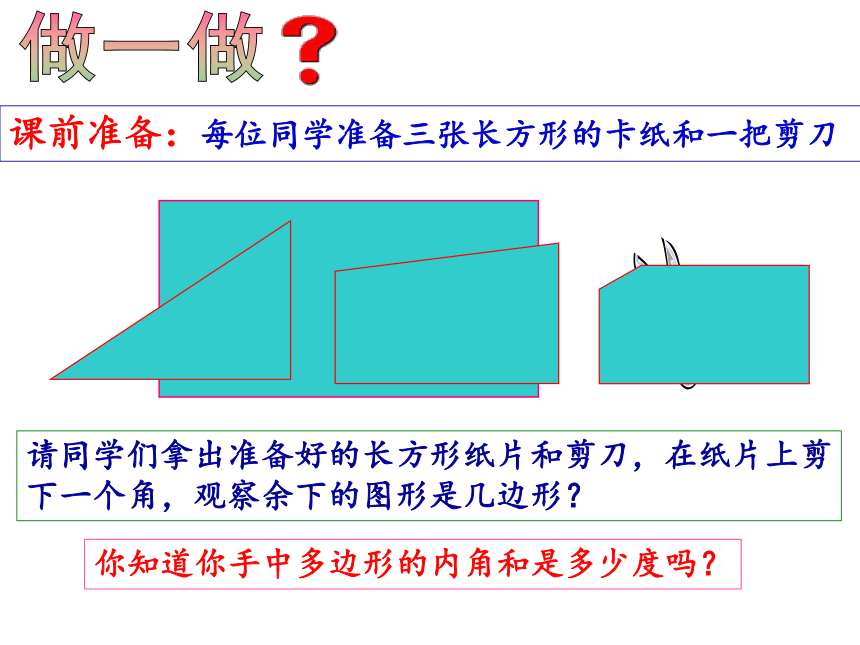
课前准备:每位同学准备三张长方形的卡纸和一把剪刀
请同学们拿出准备好的长方形纸片和剪刀,在纸片上剪下一个角,观察余下的图形是几边形?
你知道你手中多边形的内角和是多少度吗?
11.3.2 多边形的内角和
人教版八年级上册
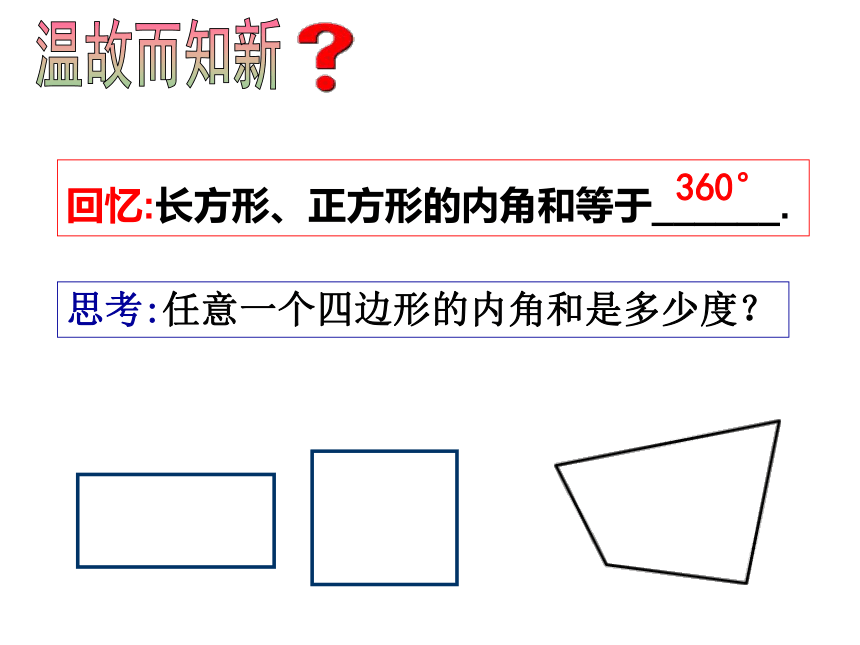
回忆:长方形、正方形的内角和等于______.
思考:任意一个四边形的内角和是多少度?
360°
小组合作:拿出你刚刚剪下的四边形纸片,利用手中的工具(剪刀 直尺 量角器)猜想出它的内角和?
方法1.量一量、算一算
猜想四边形四个内角和
方法2.剪一剪、拼一拼
猜想四边形内角和
猜想:∠A+∠B+∠C+∠D= 360°
请利用三角形内角和定理及平角、周角等相关知识验证你的猜想。
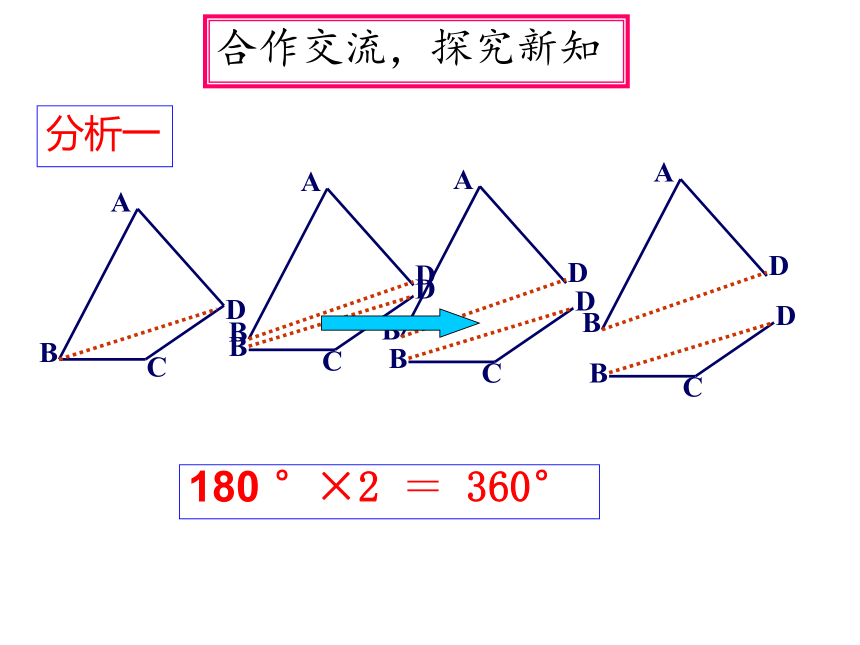
180 °×2 = 360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
分析一
合作交流,探究新知
180 °×3 -180 °=360°
A
B
C
D
A
D
E
E
A
B
C
D
E
A
B
E
A
D
E
C
E
D
合作交流,探究新知
分析二
A
D
C
B
. p
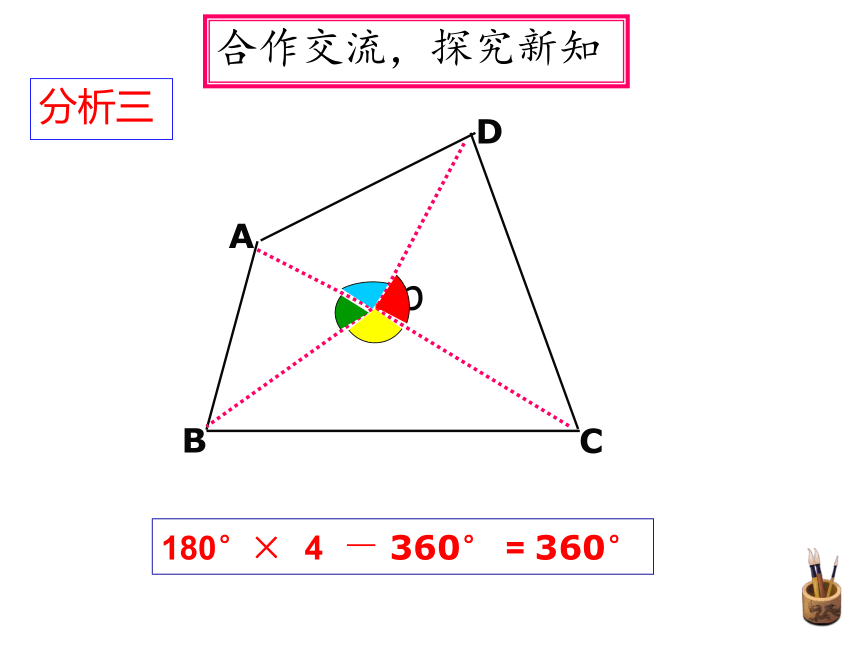
180°× 4 - 360° = 360°
合作交流,探究新知
分析三
A
D
C
B
.p
180° × 3 - 180° = 360°
合作交流,探究新知
分析四
请选择你喜欢的一种方法探索五边形、六边形、七边形……n边形的内角和并填写下表
归纳思路:
从四边形的的顶点、边上、内部、外部的任意一点出发,将四边形分割转化成若干个三角形,再利用三角形的内角和为180°及平角、周角的定义来求得,这种化复杂为简单,化未知为已知的转化思想是数学中常用的数学方法。
多边形的边数
多边形的内角和
探究规律
3
4
5
6
7
.……
……
……
n
n边形内角和公式:
n边形的内角和等于(n-2)·180°(n≥3)
总结成果,发现规律
180°
360°
540°
720°
900°
(3-2)× 180°
(4-2)× 180°
(5-2)× 180°
(6-2)× 180°
(7-2)× 180°
(n-2)× 180°
1.当多边形的边数每增加1的时候,内角和就会增加180°
学生
发现
2.多边形的内角和=(边数-2 ) × 180°
(1)上课开始时剪出的四边形的内角和是 ___,五边形 内角和是___。
(2)一个多边形的内角和是1800°它是___边。
(3)一个多边形每个内角都等于108°,则这个多边形
是 ___边形。
(4)四边形ABCD中,∠A、∠B、∠C、∠D的度数之比为
1: 3::3:5,则∠D等于___。
小试身手
例题解析 巩固新知
例1:如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补。
已知:四边形ABCD中∠A+∠C=180°
求:∠B与∠D的关系.
解:∵∠A+∠B+∠C+∠D= 360°
∴∠B+∠D =360°-(∠A+∠C)
=360°-180°
=180°
A
B
C
D
E
F
如图:在长方形ABCD中,BE平分∠ABC,交CD于点E,DF平分∠ADC,交AB于点F.问:DF是否平行于BE?请说明理由。
变式训练:若将上图的长方形ABCD改成如图∠A=∠C=900的四边形,其他条件不变。问:DF是否还平行于BE?请说明理由。
3
4
1
2
E
F
在变式中创新
2
1
3
4
5
5
例2:如图:在六边形的每个顶点处各取一个外角,这些 外角的和叫做六边形的外角和。
利用外角与相邻内角的关系,求出六边形的外角和。
A
B
C
D
E
F
1
2
3
4
5
6
解:
∵六边形的任何一个外角加上它
相邻的内角都等于180°
∴总和等于6×180°
∵六边形的内角和=(6-2×180°
∴外角和= 6×180°-(6-2×180°
= 2×180°
= 360°
n边形的外角和是多少度呢?
∵n边形的外角与它相邻的内角是邻补角
∴n边形的外角和加内角和等于n·180°
∵内角和=(n-2)·180°
∴外角和为=n·180°-(n-2)·180°=360°
结论:n边形的外角和都等于360°
猜想与说理
问题:小明每天坚持跑步,右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图.请你观察并思考他每跑完一圈,身体转过的角度之和是多少?
A
B
C
D
E
1
2
3
4
5
现学现用,回归生活
回 顾 与 反 思
让我们的认识升华
这节课我们探究了哪些问题?
在探究过程中,你学到了哪些新的知识?
通过这个探究过程,你学到了哪些数学思想?
①n边形的内角和=(n-2)·180° n边形外角和等于360°
②如果四边形的一组对角互补,那么另一组对角也互补;
③让学生经历观察-实验-猜想-推理-归纳的过程,发展学生合情推理能力;从具体的四边形的内角和研究出发,让学生尝试从不同角度分析问题,利用多种方法来证明 ;通过类比的方法探索五边形、六边形……到n边形内角和公式的归纳,体会化归思想和从具体到抽象的研究问题的方法。
④探究过程运用的数学思想:转化的思想、方程思想、类比的思想、归纳的思想。
反思盘点,整合新知
课堂检测,强化新知
(1)四边形ABCD中∠A与∠C互补,∠B=80°∠D=____
(2)十边形的内角和为___度,外角和为___度。
(3)一个多边形的内角和为1080°,则边数为____。
(4)我国的国旗上的闪闪红星是五角星,请求出五
个角的度数之和?
必做题:教科书第24-25页习题11.3
第1、2、3、4、5 、6题
选做题:教科书第24-25页习题11.3
第9、10题
拓展题:如图:某居民小区搞绿化,分别在三角形、四边形、五边形的广场各角修建半径为1米的花坛.你能求出花坛的面积吗?
(结果保留π)
课后作业布置
人教版八年级(上册)
课前准备:每位同学准备三张长方形的卡纸和一把剪刀
请同学们拿出准备好的长方形纸片和剪刀,在纸片上剪下一个角,观察余下的图形是几边形?
你知道你手中多边形的内角和是多少度吗?
11.3.2 多边形的内角和
人教版八年级上册
回忆:长方形、正方形的内角和等于______.
思考:任意一个四边形的内角和是多少度?
360°
小组合作:拿出你刚刚剪下的四边形纸片,利用手中的工具(剪刀 直尺 量角器)猜想出它的内角和?
方法1.量一量、算一算
猜想四边形四个内角和
方法2.剪一剪、拼一拼
猜想四边形内角和
猜想:∠A+∠B+∠C+∠D= 360°
请利用三角形内角和定理及平角、周角等相关知识验证你的猜想。
180 °×2 = 360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
分析一
合作交流,探究新知
180 °×3 -180 °=360°
A
B
C
D
A
D
E
E
A
B
C
D
E
A
B
E
A
D
E
C
E
D
合作交流,探究新知
分析二
A
D
C
B
. p
180°× 4 - 360° = 360°
合作交流,探究新知
分析三
A
D
C
B
.p
180° × 3 - 180° = 360°
合作交流,探究新知
分析四
请选择你喜欢的一种方法探索五边形、六边形、七边形……n边形的内角和并填写下表
归纳思路:
从四边形的的顶点、边上、内部、外部的任意一点出发,将四边形分割转化成若干个三角形,再利用三角形的内角和为180°及平角、周角的定义来求得,这种化复杂为简单,化未知为已知的转化思想是数学中常用的数学方法。
多边形的边数
多边形的内角和
探究规律
3
4
5
6
7
.……
……
……
n
n边形内角和公式:
n边形的内角和等于(n-2)·180°(n≥3)
总结成果,发现规律
180°
360°
540°
720°
900°
(3-2)× 180°
(4-2)× 180°
(5-2)× 180°
(6-2)× 180°
(7-2)× 180°
(n-2)× 180°
1.当多边形的边数每增加1的时候,内角和就会增加180°
学生
发现
2.多边形的内角和=(边数-2 ) × 180°
(1)上课开始时剪出的四边形的内角和是 ___,五边形 内角和是___。
(2)一个多边形的内角和是1800°它是___边。
(3)一个多边形每个内角都等于108°,则这个多边形
是 ___边形。
(4)四边形ABCD中,∠A、∠B、∠C、∠D的度数之比为
1: 3::3:5,则∠D等于___。
小试身手
例题解析 巩固新知
例1:如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补。
已知:四边形ABCD中∠A+∠C=180°
求:∠B与∠D的关系.
解:∵∠A+∠B+∠C+∠D= 360°
∴∠B+∠D =360°-(∠A+∠C)
=360°-180°
=180°
A
B
C
D
E
F
如图:在长方形ABCD中,BE平分∠ABC,交CD于点E,DF平分∠ADC,交AB于点F.问:DF是否平行于BE?请说明理由。
变式训练:若将上图的长方形ABCD改成如图∠A=∠C=900的四边形,其他条件不变。问:DF是否还平行于BE?请说明理由。
3
4
1
2
E
F
在变式中创新
2
1
3
4
5
5
例2:如图:在六边形的每个顶点处各取一个外角,这些 外角的和叫做六边形的外角和。
利用外角与相邻内角的关系,求出六边形的外角和。
A
B
C
D
E
F
1
2
3
4
5
6
解:
∵六边形的任何一个外角加上它
相邻的内角都等于180°
∴总和等于6×180°
∵六边形的内角和=(6-2×180°
∴外角和= 6×180°-(6-2×180°
= 2×180°
= 360°
n边形的外角和是多少度呢?
∵n边形的外角与它相邻的内角是邻补角
∴n边形的外角和加内角和等于n·180°
∵内角和=(n-2)·180°
∴外角和为=n·180°-(n-2)·180°=360°
结论:n边形的外角和都等于360°
猜想与说理
问题:小明每天坚持跑步,右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图.请你观察并思考他每跑完一圈,身体转过的角度之和是多少?
A
B
C
D
E
1
2
3
4
5
现学现用,回归生活
回 顾 与 反 思
让我们的认识升华
这节课我们探究了哪些问题?
在探究过程中,你学到了哪些新的知识?
通过这个探究过程,你学到了哪些数学思想?
①n边形的内角和=(n-2)·180° n边形外角和等于360°
②如果四边形的一组对角互补,那么另一组对角也互补;
③让学生经历观察-实验-猜想-推理-归纳的过程,发展学生合情推理能力;从具体的四边形的内角和研究出发,让学生尝试从不同角度分析问题,利用多种方法来证明 ;通过类比的方法探索五边形、六边形……到n边形内角和公式的归纳,体会化归思想和从具体到抽象的研究问题的方法。
④探究过程运用的数学思想:转化的思想、方程思想、类比的思想、归纳的思想。
反思盘点,整合新知
课堂检测,强化新知
(1)四边形ABCD中∠A与∠C互补,∠B=80°∠D=____
(2)十边形的内角和为___度,外角和为___度。
(3)一个多边形的内角和为1080°,则边数为____。
(4)我国的国旗上的闪闪红星是五角星,请求出五
个角的度数之和?
必做题:教科书第24-25页习题11.3
第1、2、3、4、5 、6题
选做题:教科书第24-25页习题11.3
第9、10题
拓展题:如图:某居民小区搞绿化,分别在三角形、四边形、五边形的广场各角修建半径为1米的花坛.你能求出花坛的面积吗?
(结果保留π)
课后作业布置
