2020-2021学年人教版数学八年级上册11.3.2多边形的内角和课件2(共27张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.3.2多边形的内角和课件2(共27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览




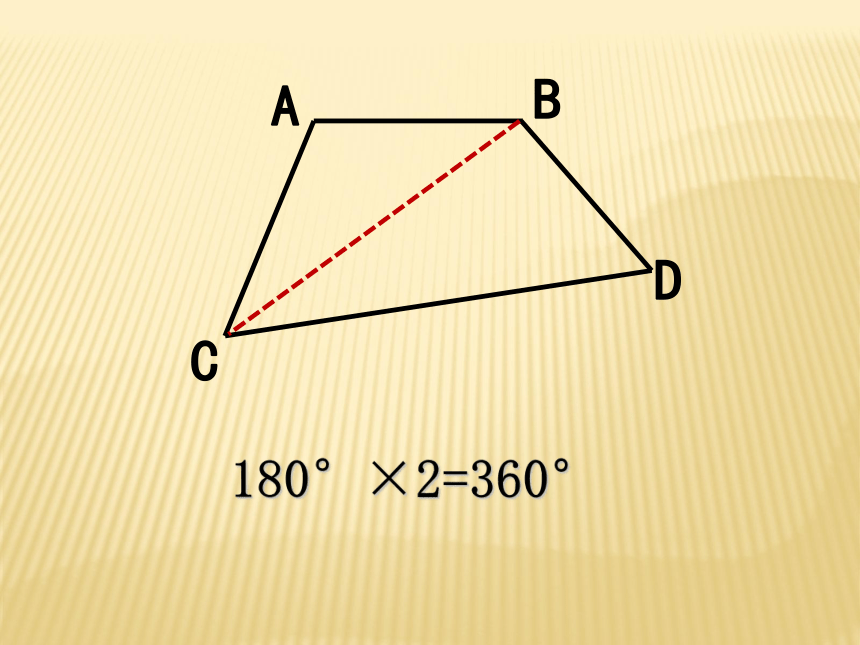



文档简介
11.3.2多边形的内角和
2011人教版八年级上册
三角形的内角和等于180°
长方形,正方形的内角和都是360°
猜猜看:任意四边形的内角和等于多少?
活动1:探索任意四边形的内角和等于多少度?你是怎样得到的?
180°×2=360°
A
B
C
D
试想:三角形内角和为180°,
四边形内角和为360 °,
任意多边形的内角和等于多少?
几何画板演示四边形、五边形、
六边形随着内角的变化,内角和
变化情况。
我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
p
多边形的内角和
分成的三角形个数
n
…
6
5
4
3
多边形的边数
n-2
(n-2)·180°
1
2
3
4
180°
360°
540°
720°
…
…
A
B
C
A
B
C
D
A
B
C
D
E
A
B
C
E
D
F
探究得结论:
解:如图所示,四边形ABCD中,
∠A+∠C= 180°
∵∠A+∠B+ ∠C+ ∠D=(4-2)×180。=360°
∴∠B+∠D = 360° -(∠A+∠C )
= 360° - 180°
= 180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
A
D
C
B
n边形内角和=180。×(n-2)
解:七边形内角和:
180。×(7-2)=900。
十边形内角和:
180。×(10-2)=1440。
提示
解1:1260。÷180。+2
=7+2
=9
n边形内角和÷180。+2
解2:设这个多边形是n边形,依题意得,
180。×(n-2)=1260。
解得:n=9
答:这个多边形是九边形。
2x。
x。
120。
150。
x。
140。
x。
解:140 。 +90。+x。+x。=180。×(4-2)
230。+2x。=360。
2x。= 130。
x°=65。
解:120。+150。+90。+ x。+2x。=180。×(5-2)
360。+3x。=540。
3x。=180。
x。=60。
有一把锋利的“锯”,把一张桌子(四边形)一个角锯下去,剩下的桌子是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
M
N
例题探究:2、如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
A
B
C
D
E
F
1
2
3
4
5
6
结论:六边形外角和等于360°
多边形
图形
多边形的外角和
三角形
四边形
五边形
…
…
……
n边形
3×180°-(3-2)×180°=360°
4×180°-(4-2)×180°=360°
5×180°-(5-2)×180°=360°
n×180o-(n-2)×180°=360°
探究任意多边形的外角和
活动3:
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。
多边形外角和为360°
练一练
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°= 360°
n= 12
n边形外角和= 360°
练一练
2、正五边形的每一个外角等于____,每一个内角等于_____ .
5 x=360
x=72
108°
72°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108 °
1、快速抢答,熟悉公式
(1)八边形的内角和是 。(1分)
(2)一个多边形的内角和是1800°它是 边 形。 (1分)
(3)如果一个多边形的每一个外角等于15°,则这个多边形的边数是_____ (1分)
1080°
十二
24
闯关一:基础过关
2、在四边形ABCD中,∠A=120度,∠B:∠C:∠D = 3:4:5,则∠B= ,∠C = , ∠D = 。(2分)
3、如果一个四边形的一组对角互补,那么另一组对角的关系是 。 (2分)
60°
100°
80°
互补
4、正n边形的每一个外角等于___.每一个内角等于 (2分)
5、一个多边形的各内角都等于120°,它是___ 边形。 (2分)
360°
n
(n-2) ×180 °
n
六
闯关二:能力提升
6、 一个多边形内角和是外角和的2倍,它是几边形?(2分)
解: 设多边形的边数为n,根据题意可得
(n-2)?180° = 360°×2
解得:n = 6
答: 它是六边形。
闯关三:综合应用
1.n边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法:转化
多边形 三角形
→
最后一关:我的学习收获(2分)
2011人教版八年级上册
三角形的内角和等于180°
长方形,正方形的内角和都是360°
猜猜看:任意四边形的内角和等于多少?
活动1:探索任意四边形的内角和等于多少度?你是怎样得到的?
180°×2=360°
A
B
C
D
试想:三角形内角和为180°,
四边形内角和为360 °,
任意多边形的内角和等于多少?
几何画板演示四边形、五边形、
六边形随着内角的变化,内角和
变化情况。
我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
p
多边形的内角和
分成的三角形个数
n
…
6
5
4
3
多边形的边数
n-2
(n-2)·180°
1
2
3
4
180°
360°
540°
720°
…
…
A
B
C
A
B
C
D
A
B
C
D
E
A
B
C
E
D
F
探究得结论:
解:如图所示,四边形ABCD中,
∠A+∠C= 180°
∵∠A+∠B+ ∠C+ ∠D=(4-2)×180。=360°
∴∠B+∠D = 360° -(∠A+∠C )
= 360° - 180°
= 180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
A
D
C
B
n边形内角和=180。×(n-2)
解:七边形内角和:
180。×(7-2)=900。
十边形内角和:
180。×(10-2)=1440。
提示
解1:1260。÷180。+2
=7+2
=9
n边形内角和÷180。+2
解2:设这个多边形是n边形,依题意得,
180。×(n-2)=1260。
解得:n=9
答:这个多边形是九边形。
2x。
x。
120。
150。
x。
140。
x。
解:140 。 +90。+x。+x。=180。×(4-2)
230。+2x。=360。
2x。= 130。
x°=65。
解:120。+150。+90。+ x。+2x。=180。×(5-2)
360。+3x。=540。
3x。=180。
x。=60。
有一把锋利的“锯”,把一张桌子(四边形)一个角锯下去,剩下的桌子是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
M
N
例题探究:2、如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
A
B
C
D
E
F
1
2
3
4
5
6
结论:六边形外角和等于360°
多边形
图形
多边形的外角和
三角形
四边形
五边形
…
…
……
n边形
3×180°-(3-2)×180°=360°
4×180°-(4-2)×180°=360°
5×180°-(5-2)×180°=360°
n×180o-(n-2)×180°=360°
探究任意多边形的外角和
活动3:
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。
多边形外角和为360°
练一练
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°= 360°
n= 12
n边形外角和= 360°
练一练
2、正五边形的每一个外角等于____,每一个内角等于_____ .
5 x=360
x=72
108°
72°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108 °
1、快速抢答,熟悉公式
(1)八边形的内角和是 。(1分)
(2)一个多边形的内角和是1800°它是 边 形。 (1分)
(3)如果一个多边形的每一个外角等于15°,则这个多边形的边数是_____ (1分)
1080°
十二
24
闯关一:基础过关
2、在四边形ABCD中,∠A=120度,∠B:∠C:∠D = 3:4:5,则∠B= ,∠C = , ∠D = 。(2分)
3、如果一个四边形的一组对角互补,那么另一组对角的关系是 。 (2分)
60°
100°
80°
互补
4、正n边形的每一个外角等于___.每一个内角等于 (2分)
5、一个多边形的各内角都等于120°,它是___ 边形。 (2分)
360°
n
(n-2) ×180 °
n
六
闯关二:能力提升
6、 一个多边形内角和是外角和的2倍,它是几边形?(2分)
解: 设多边形的边数为n,根据题意可得
(n-2)?180° = 360°×2
解得:n = 6
答: 它是六边形。
闯关三:综合应用
1.n边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法:转化
多边形 三角形
→
最后一关:我的学习收获(2分)
