人教版 九年级数学上册 21.2.2解一元二次方程——公式法 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版 九年级数学上册 21.2.2解一元二次方程——公式法 同步练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 339.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 06:39:18 | ||
图片预览




文档简介
21.2.2解一元二次方程——公式法
一、单选题
1.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是(
)
A.
B.
C.且
D.
2.方程的根为(
)
A.
B.
C.
D.
3.若关于的一元二次方程没有实数根,则的取值范围是(
)
A.
B.
C.
D.
4.一元二次方程4x2+1=﹣4x的根的情况是(
)
A.只有一个实数根
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
5.下列方程中,有实数解的是(
)
A.
B.
C.
D.
6.已知关于的一元二次方程,其中,在数轴上的对应点如图所示,则这个方程的根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.只有一个实数根
7.若直角三角形的两边长分别是方程的两根,则该直角三角形的面积是(
)
A.6
B.12
C.12或
D.6或
8.关于的方程有实数根,则的取值范围是(
)
A.且
B.且
C.
D.
9.关于x的一元二次方程有实数根,则点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.将4个数、、、排成2行、2列,两边各加一条竖直线记成,定义.例如.则方程的根的情况为(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.只有一个实数根
二、填空题
11.关于x的一元二次方程有实数根,则m的取值范围是__.
12.关于的一元二次方程有两个不相等实数根,则的值为____________.
13.在实数范围内定义一种运算“
”,其规则为a
b=a2-b2,根据这个规则,方程(x+1)
3=0的解为______.
14.关于x的一元二次方程(a+1)x2+bx+1=0有两个相等的实数根,则代数式8a﹣2b2+6的值是__.
15.若一元二次方程无解,则c的取值范围为_________.
三、解答题
16.解下列一元二次方程:
(1)
(2)
(3)
(4)
17.关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根为负数,求m的取值范围.
18.已知关于x的一元二次方程x2﹣(k+1)x+2k﹣3=0.
(1)求证:无论k为何实数,方程总有两个不相等的实数根;
(2)等腰三角形ABC中,AB=3,若AC、BC为方程x2﹣(k+1)x+2k﹣3=0的两个实数根,求k的值.
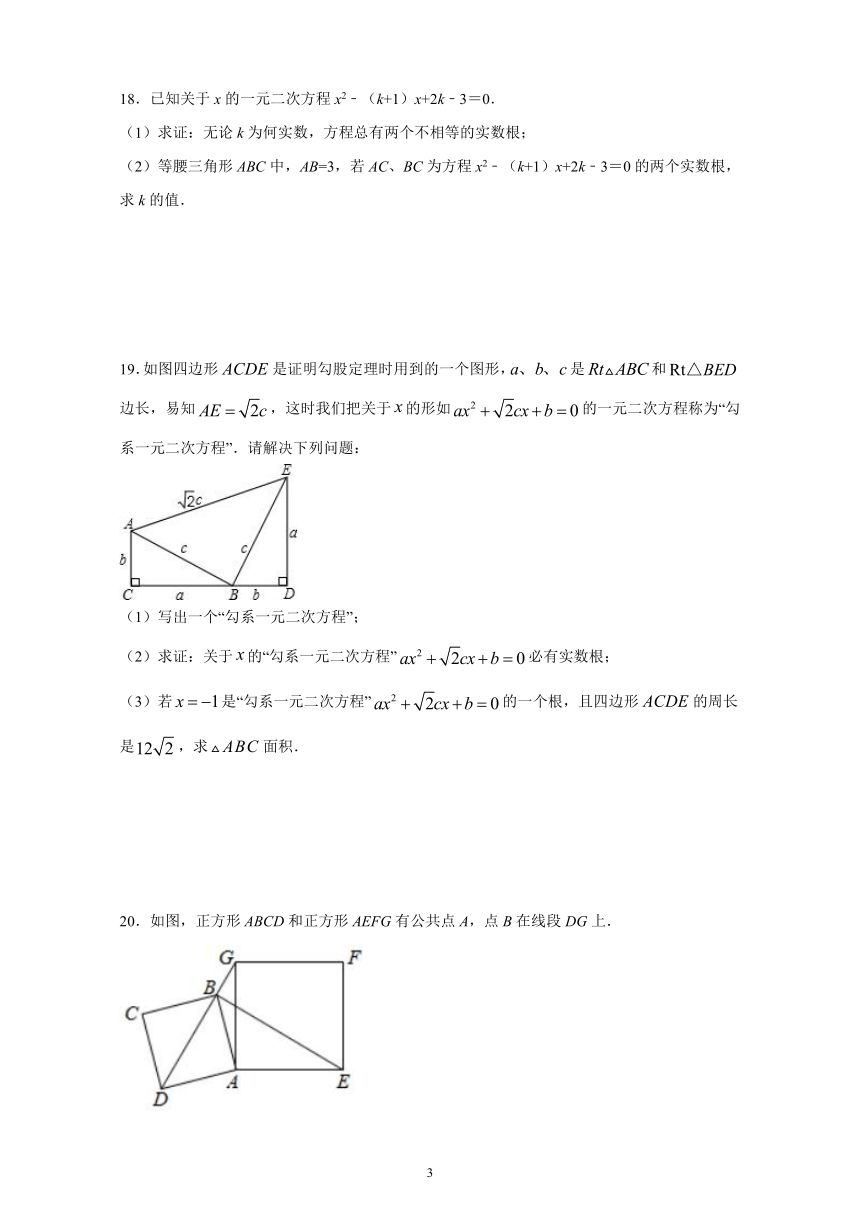
19.如图四边形是证明勾股定理时用到的一个图形,是和边长,易知,这时我们把关于的形如的一元二次方程称为“勾系一元二次方程”.请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于的“勾系一元二次方程”必有实数根;
(3)若是“勾系一元二次方程”的一个根,且四边形的周长是,求面积.
20.如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.
(1)判断DG与BE的位置关系,并说明理由;
(2)若正方形ABCD的边长为1,正方形AEFG的边长为,求BE的长.
参考答案
1.D
解:由关于x的一元二次方程有两个不相等的实数根,可得:
,
解得:;
故选D.
2.D
解:,
变形得:,
开方得:,
故选:D.
3.A
解:∵关于x的一元二次方程x2+k-3=0没有实数根,
∴Δ=02-4×1×(k-3)=-4k+12<0,
∴k的取值范围是k>3;
故选:A.
4.C
解:方程4x2+1=-4x化为一般形式为4x2+4x+1=0,
∴Δ=42-4×4×1=0,
∴该方程有两个相等的实数根,
故选:C.
5.D
解:,
,
,
无实数解;
,
,
,
无实数解;
,
△,
无实数解;
,
解得,
有实数解,
故选:D.
6.A
解:由数轴可知:,;
∴;
∴有两个不相等的实数根
故选:A
7.D
解:解方程得,
当3和4分别为直角三角形的直角边时,面积为;
当4为斜边,3为直角边时根据勾股定理得另一直角边为,面积为;
则该直角三角形的面积是6或,
故选:D.
8.D
解:当方程为一元二次方程时,
∵关于的方程有实数根,
∴,且
,
解得,且,
当方程为一元一次方程时,k=1,方程有实根
综上,
故选:D.
9.B
解:∵是一元二次方程,且有实数根,
∴m-1≠0且,
解得:且m≠1,
∴m-3<0,-m+4>0,
∴在第二象限,
故选B.
10.B
解:∵
∴x2-6x=-9,即x2-6x+9=0
∵△=(-6)2-4×9×1=0
∴该方程有两个相等的实数根.
故选:B.
11.m≤2且m≠1
解:∵要保证方程为二次方程故m-1≠0得m≠1,
又∵方程有实数根,
∴,
解得m≤2,
故答案为:m≤2且m≠1.
12.且
解:根据题意得,
解得:且.
故答案为:且.
13.x1=2,x2=-4
解:根据新运算规则,可化为
∴
∴或
∴,
故答案为,
14.-2
解:根据题意得a+1≠0且△=b2?4×(a+1)=0,即b2?4a?4=0,
∴b2?4a=4,
∴原式=?2(b2?4a)+6=?2×4+6=?2,
故答案为?2.
15.
解:关于x的一元二次方程无解,
∵,,,
∴,
解得,
∴的取值范围是.
故答案为:.
16.(1);(2);(3);(4)
解:(1),
∴,
∴或,
解得:;
(2),
∵a=2,b=-4,c=-7,
∴△=16-4×2×(-7)=72,
∴x=,
解得:;
(3),
∵a=1,b=1,c=-1,
∴△=1-4×1×(-1)=5,
∴x=,
解得:;
(4),
∴,
∴或,
解得:.
17.(1)见解析;(2)
(1)证明:
.
∵,
∴方程总有两个实数根.
(2)解:∵,
∴
∵方程有一个根为负数,
∴m
<
0.
18.(1)见解析;(2)k=3
解:(1)∵△=[﹣(k+1)]2﹣4×1×(2k﹣3)
=k2+2k+1﹣8k+12
=(k-3)2+4,
∵无论k为何实数,(k-3)2≥0,
∴(k-3)2+4>0,
∴无论k为何实数,方程总有两个不相等的实数根;
(2)∵AC、BC为方程x2﹣(k+1)x+2k﹣3=0的两个实数根,
由(1)可得,AC≠BC,
∵△ABC为等腰三角形,
∴AC=AB=3或BC=AB=3,
∴方程x2﹣(k+1)x+2k﹣3=0必有一根为x=3,
∴32﹣3(k+1)+2k﹣3=0,
解得k=3.
19.(1);(2)见解析;(3)4
解:(1)当,,时
勾系一元二次方程为;
(2)证明:根据题意,得
△
即△,
勾系一元二次方程必有实数根;
(3)当时,有,即,
,即,
,
,
,,
,
,
.
20.(1)DG⊥BE,理由见解析;(2)BE的长为.
(1)DG⊥BE,
理由如下:∵四边形ABCD,四边形AEFG是正方形,
∴AB=AD,∠DAB=∠GAE,AE=AG,∠ADB=∠ABD=45°,
∴∠DAG=∠BAE,
在△DAG和△BAE中,
,
∴△DAG≌△BAE(SAS).
∴DG=BE,∠ADG=∠ABE=45°,
∴∠ABD+∠ABE=90°,即∠GBE=90°.
∴DG⊥BE;
(2)连接GE,
∵正方形ABCD的边长为1,正方形AEFG的边长为,
∴BD=,GE=2,设BE=x,
∵DG=BE,
∴BG=x﹣,
在Rt△BGE中,利用勾股定理可得:,
∴
∴x=或x=(舍去),
∴BE的长为.
一、单选题
1.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是(
)
A.
B.
C.且
D.
2.方程的根为(
)
A.
B.
C.
D.
3.若关于的一元二次方程没有实数根,则的取值范围是(
)
A.
B.
C.
D.
4.一元二次方程4x2+1=﹣4x的根的情况是(
)
A.只有一个实数根
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
5.下列方程中,有实数解的是(
)
A.
B.
C.
D.
6.已知关于的一元二次方程,其中,在数轴上的对应点如图所示,则这个方程的根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.只有一个实数根
7.若直角三角形的两边长分别是方程的两根,则该直角三角形的面积是(
)
A.6
B.12
C.12或
D.6或
8.关于的方程有实数根,则的取值范围是(
)
A.且
B.且
C.
D.
9.关于x的一元二次方程有实数根,则点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.将4个数、、、排成2行、2列,两边各加一条竖直线记成,定义.例如.则方程的根的情况为(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.只有一个实数根
二、填空题
11.关于x的一元二次方程有实数根,则m的取值范围是__.
12.关于的一元二次方程有两个不相等实数根,则的值为____________.
13.在实数范围内定义一种运算“
”,其规则为a
b=a2-b2,根据这个规则,方程(x+1)
3=0的解为______.
14.关于x的一元二次方程(a+1)x2+bx+1=0有两个相等的实数根,则代数式8a﹣2b2+6的值是__.
15.若一元二次方程无解,则c的取值范围为_________.
三、解答题
16.解下列一元二次方程:
(1)
(2)
(3)
(4)
17.关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根为负数,求m的取值范围.
18.已知关于x的一元二次方程x2﹣(k+1)x+2k﹣3=0.
(1)求证:无论k为何实数,方程总有两个不相等的实数根;
(2)等腰三角形ABC中,AB=3,若AC、BC为方程x2﹣(k+1)x+2k﹣3=0的两个实数根,求k的值.
19.如图四边形是证明勾股定理时用到的一个图形,是和边长,易知,这时我们把关于的形如的一元二次方程称为“勾系一元二次方程”.请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于的“勾系一元二次方程”必有实数根;
(3)若是“勾系一元二次方程”的一个根,且四边形的周长是,求面积.
20.如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.
(1)判断DG与BE的位置关系,并说明理由;
(2)若正方形ABCD的边长为1,正方形AEFG的边长为,求BE的长.
参考答案
1.D
解:由关于x的一元二次方程有两个不相等的实数根,可得:
,
解得:;
故选D.
2.D
解:,
变形得:,
开方得:,
故选:D.
3.A
解:∵关于x的一元二次方程x2+k-3=0没有实数根,
∴Δ=02-4×1×(k-3)=-4k+12<0,
∴k的取值范围是k>3;
故选:A.
4.C
解:方程4x2+1=-4x化为一般形式为4x2+4x+1=0,
∴Δ=42-4×4×1=0,
∴该方程有两个相等的实数根,
故选:C.
5.D
解:,
,
,
无实数解;
,
,
,
无实数解;
,
△,
无实数解;
,
解得,
有实数解,
故选:D.
6.A
解:由数轴可知:,;
∴;
∴有两个不相等的实数根
故选:A
7.D
解:解方程得,
当3和4分别为直角三角形的直角边时,面积为;
当4为斜边,3为直角边时根据勾股定理得另一直角边为,面积为;
则该直角三角形的面积是6或,
故选:D.
8.D
解:当方程为一元二次方程时,
∵关于的方程有实数根,
∴,且
,
解得,且,
当方程为一元一次方程时,k=1,方程有实根
综上,
故选:D.
9.B
解:∵是一元二次方程,且有实数根,
∴m-1≠0且,
解得:且m≠1,
∴m-3<0,-m+4>0,
∴在第二象限,
故选B.
10.B
解:∵
∴x2-6x=-9,即x2-6x+9=0
∵△=(-6)2-4×9×1=0
∴该方程有两个相等的实数根.
故选:B.
11.m≤2且m≠1
解:∵要保证方程为二次方程故m-1≠0得m≠1,
又∵方程有实数根,
∴,
解得m≤2,
故答案为:m≤2且m≠1.
12.且
解:根据题意得,
解得:且.
故答案为:且.
13.x1=2,x2=-4
解:根据新运算规则,可化为
∴
∴或
∴,
故答案为,
14.-2
解:根据题意得a+1≠0且△=b2?4×(a+1)=0,即b2?4a?4=0,
∴b2?4a=4,
∴原式=?2(b2?4a)+6=?2×4+6=?2,
故答案为?2.
15.
解:关于x的一元二次方程无解,
∵,,,
∴,
解得,
∴的取值范围是.
故答案为:.
16.(1);(2);(3);(4)
解:(1),
∴,
∴或,
解得:;
(2),
∵a=2,b=-4,c=-7,
∴△=16-4×2×(-7)=72,
∴x=,
解得:;
(3),
∵a=1,b=1,c=-1,
∴△=1-4×1×(-1)=5,
∴x=,
解得:;
(4),
∴,
∴或,
解得:.
17.(1)见解析;(2)
(1)证明:
.
∵,
∴方程总有两个实数根.
(2)解:∵,
∴
∵方程有一个根为负数,
∴m
<
0.
18.(1)见解析;(2)k=3
解:(1)∵△=[﹣(k+1)]2﹣4×1×(2k﹣3)
=k2+2k+1﹣8k+12
=(k-3)2+4,
∵无论k为何实数,(k-3)2≥0,
∴(k-3)2+4>0,
∴无论k为何实数,方程总有两个不相等的实数根;
(2)∵AC、BC为方程x2﹣(k+1)x+2k﹣3=0的两个实数根,
由(1)可得,AC≠BC,
∵△ABC为等腰三角形,
∴AC=AB=3或BC=AB=3,
∴方程x2﹣(k+1)x+2k﹣3=0必有一根为x=3,
∴32﹣3(k+1)+2k﹣3=0,
解得k=3.
19.(1);(2)见解析;(3)4
解:(1)当,,时
勾系一元二次方程为;
(2)证明:根据题意,得
△
即△,
勾系一元二次方程必有实数根;
(3)当时,有,即,
,即,
,
,
,,
,
,
.
20.(1)DG⊥BE,理由见解析;(2)BE的长为.
(1)DG⊥BE,
理由如下:∵四边形ABCD,四边形AEFG是正方形,
∴AB=AD,∠DAB=∠GAE,AE=AG,∠ADB=∠ABD=45°,
∴∠DAG=∠BAE,
在△DAG和△BAE中,
,
∴△DAG≌△BAE(SAS).
∴DG=BE,∠ADG=∠ABE=45°,
∴∠ABD+∠ABE=90°,即∠GBE=90°.
∴DG⊥BE;
(2)连接GE,
∵正方形ABCD的边长为1,正方形AEFG的边长为,
∴BD=,GE=2,设BE=x,
∵DG=BE,
∴BG=x﹣,
在Rt△BGE中,利用勾股定理可得:,
∴
∴x=或x=(舍去),
∴BE的长为.
同课章节目录
