人教版八年级上册:11.3 多边形及其内角和 课后作业 (word版,含解析)
文档属性
| 名称 | 人教版八年级上册:11.3 多边形及其内角和 课后作业 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 15:35:01 | ||
图片预览



文档简介
11.3 多边形及其内角和 课后作业
一.选择题
1.如图,在五边形ABCDE中,AB∥CD,∠A=135°,∠C=60°,∠D=150°,则∠E的大小为( )
A.60° B.65° C.70° D.75°
2.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.边数为n的多边形内角和是(n﹣2)×180°
C.有一个内角是直角的三角形是直角三角形
D.三角形的中线、角平分线、高线都是线段
3.已知正多边形的一个内角为144°,则该正多边形的边数为( )
A.12 B.10 C.8 D.6
4.一个正多边形的内角和为540°,则这个正多边形的每一个内角是( )
A.120° B.108° C.90° D.60
5.如果一个正多边形的一个内角与一个外角的度数之比是7:2,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
6.如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.260° C.270° D.360°
二.填空题
7.已知正n边形的每个内角为144°,则n= .
8.已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为 .
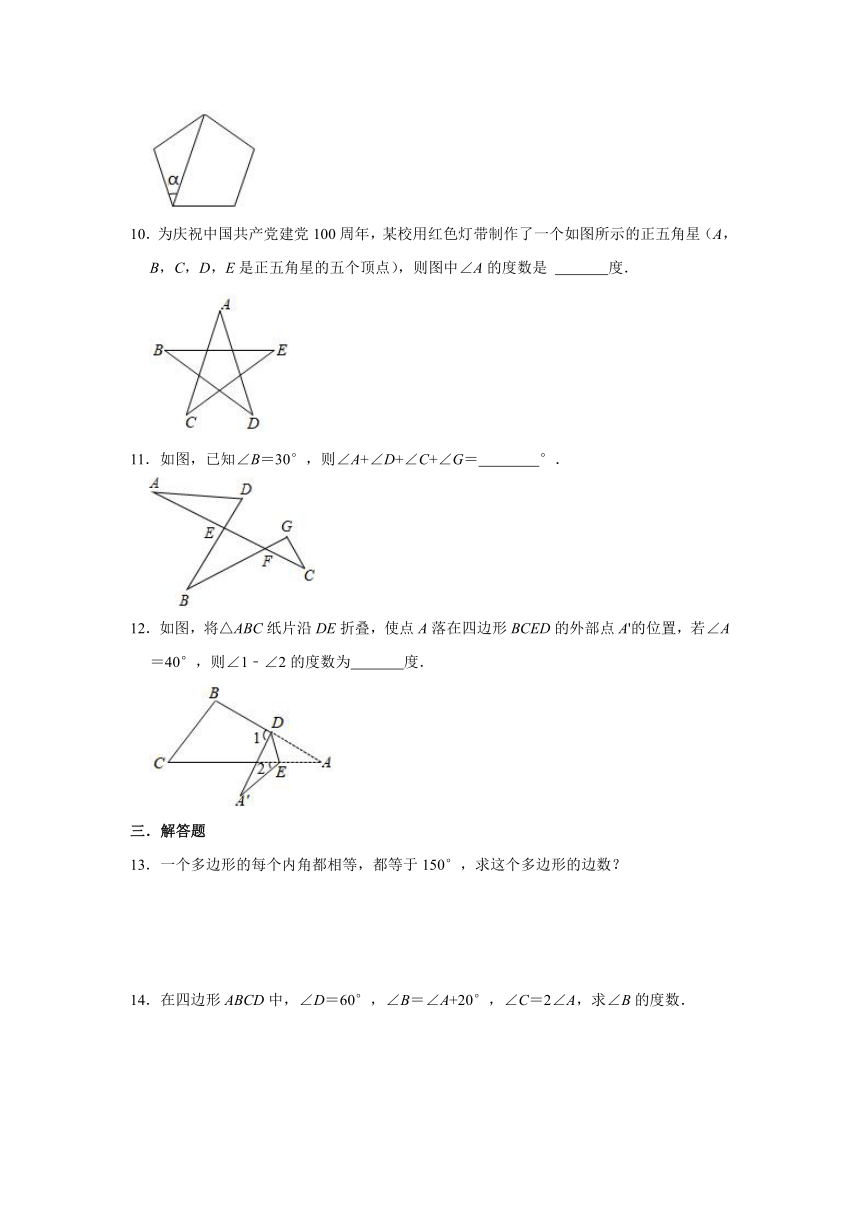
9.如图所示,正五边形中∠α的度数为 .
10.为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是 度.
11.如图,已知∠B=30°,则∠A+∠D+∠C+∠G= °.
12.如图,将△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A'的位置,若∠A=40°,则∠1﹣∠2的度数为 度.
三.解答题
13.一个多边形的每个内角都相等,都等于150°,求这个多边形的边数?
14.在四边形ABCD中,∠D=60°,∠B=∠A+20°,∠C=2∠A,求∠B的度数.
15.如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=70°,∠ACB=40°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
16.(1)已知图①中的三角形ABC,分别作AB,BC,CA的延长线BD,CE,AF,测量∠CBD,∠ACE,∠BAF的度数,并计算∠CBD+∠ACE+∠BAF.由此你有什么发现?请利用所学知识解释说明;
(2)类似地,已知图②中的四边形PQRS,分别作PQ,QR,RS,SP的延长线QG,RH,SM,PN,测量∠RQG,∠SRH,∠PSM,∠QPN的度数,并计算∠RQG+∠SRH+∠PSM+∠QPN.由此你又有什么发现?
(3)综合(1)(2)的发现,你还能进一步得到什么猜想?
参考答案
一.选择题
1.解:∵AB∥CD,
∴∠C+∠B=180°,
∵五边形ABCDE中,∠A=135°,∠D=150°,
∴∠E=540°﹣180°﹣135°﹣150°=75°.
故选:D.
2.解:A、三角形的一个外角大于与它不相邻的任何一个内角,故原说法错误,故本选项符合题意;
B、边数为n的多边形内角和是(n﹣2)×180°,说法正确,故本选项不合题意;
C、有一个内角是直角的三角形是直角三角形,说法正确,故本选项不合题意;
D、角形的中线、角平分线、高线都是线段,说法正确,故本选项不合题意;
故选:A.
3.解:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数==10,
∴这个正多边形的边数是10.
故选:B.
4.解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5.
则这个正多边形的每一个内角为540°÷5=108°.
故选:B.
5.解:设这个正多边形的边数为n,
由题意得:(n﹣2)×180=360,
解得:n=9,
故选:C.
6.解:如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故选:A.
二.填空题
7.解:由题意得正n边形的每一个外角为180°﹣144°=36°,
n=360°÷36°=10,
故答案为10.
8.解:设这个多边形的边数为n,依题意得:
(n﹣2)180°=×360°,
解得n=5.
故这个多边形的边数为5.
故答案为:5.
9.解:∵正五边形的内角为:(5﹣2)×180°÷5=108°,
∴∠α=×(180°﹣108°)=36°,
故答案为:36°.
10.解:如图,
∵正五角星中,五边形FGHMN是正五边形,
∴∠GFN=∠FNM==108°,
∴∠AFN=∠ANF=180°﹣∠GFN=180°﹣108°=72°,
∴∠A=180°﹣∠AFN﹣∠ANF=180°﹣72°﹣72°=36°.
故答案是:36.
11.解:∵∠B=30°,
∴∠BEF+∠BFE=180°﹣30°=150°,
∴∠DEF+∠GFE=360°﹣150°=210°.
∵∠DEF=∠A+∠D,∠GFE=∠C+∠G,
∴∠A+∠D+∠C+∠G=∠DEF+∠GFE=210°,
故答案为:210.
12.解:如下图所示,
∵△ABC纸片沿DE进行折叠,点A落在四边形BCED的外部点A'的位置,
∴∠4=∠5,∠3=∠2+∠DEC,
∵∠1+∠4+∠5=180°,
∴∠1+2∠4=180°,
∴∠1=180°﹣2∠4,
∵∠3+∠DEC=180°,
∴∠2=∠3﹣∠DEC=2∠3﹣180°,
∴∠1﹣∠2=180°﹣2∠4﹣2∠3+180°=360°﹣2∠4﹣2∠3=2∠A,
∴∠1﹣∠2=2×40°=80°,
故答案为:80.
三.解答题
13.解:由题意可得:180°?(n﹣2)=150°?n,
解得n=12.
故多边形是12边形.边数为12.
14.解:四边形内角和定理得:∠A+∠B+∠C+∠D=360°,
∵∠D=60°,∠B=∠A+20°,∠C=2∠A,
∴∠A+(∠A+20°)+2∠A+60°=360°,
∴∠A=70°,
∴∠B=∠A+20°=90°,
答:∠B的度数是90°.
15.解:(1)∵∠ACE=∠A+∠ABC,
∴∠ACD+∠DCE=∠A+∠ABD+∠DBC,∠DCE=∠D+∠DBC,
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE﹣∠DBC),∠D=∠DCE﹣∠DBC,
∴∠A=2∠D,
∵∠ABC=70°,∠ACB=40°,
∴∠A=180°﹣∠ABC﹣∠ACB=70°,
∴∠D=35°;
(2)∠D=(∠M+∠N﹣180°);
理由:延长BM、CN交于点A,
∵∠A+∠ANM+∠AMN=180°,∠AMN+∠BMN=180°,∠ANM+∠CNM=180°,
∴∠A=180°﹣∠ANM﹣∠AMN=180°﹣(180°﹣∠CNM)﹣(180°﹣∠BMN)=180°﹣180°+∠CNM﹣180°+∠BMN,
则∠A=∠BMN+∠CNM﹣180°,
由(1)知,∠D=∠A,
∴∠D=(∠BMN+∠CNM﹣180°).
16.解:(1)
∠CBD=138°,∠ACE=117°,∠BAF=105°,
所以∠CBD+∠ACE+∠BAF=360°,
发现:三角形中的外角和为360°,
理由:因为∠CBD+∠ABC=180°,
∠ACE+∠ACB=180°,
∠BAC+∠BAF=180°,
所以∠CBD+∠ACE+∠BAF+∠ABC+∠ACB+∠BAC=540°,
又因为∠ABC+∠ACB+∠BAC=180°,
所以∠CBD+∠ACE+∠BAF=360°;
(2)
∠RQG=125°,∠SRH=113°,∠PSM=48°,∠QPN=74°,
所以∠RQG+∠SRH+∠PSM+∠QPN=360°;
发现:在四边形的外角和是360°;
∵∠RQG+∠PQR=180°,∠SRH+∠QRS=180°,∠PSM+∠RSP=180°,∠QPN+∠QPS=180°,
∵∠RQG+∠PQR+∠SRH+∠QRS+∠PSM+∠RSP+∠QPN+∠QPS=720°,
∵∠PQR+∠QRS+∠RSP+∠QPS=360°,
∴∠RQG+∠SRH+∠PSM+∠QPN=360°.
(3)猜想:多边形的外角和和都是360°.
设多边形为n边形,则n边形的每一个内角与它相邻的外角的和为180°,
∴n边形的外角和=180°n﹣(n﹣2)×180°=180°n﹣180°n+360°=360°.
一.选择题
1.如图,在五边形ABCDE中,AB∥CD,∠A=135°,∠C=60°,∠D=150°,则∠E的大小为( )
A.60° B.65° C.70° D.75°
2.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.边数为n的多边形内角和是(n﹣2)×180°
C.有一个内角是直角的三角形是直角三角形
D.三角形的中线、角平分线、高线都是线段
3.已知正多边形的一个内角为144°,则该正多边形的边数为( )
A.12 B.10 C.8 D.6
4.一个正多边形的内角和为540°,则这个正多边形的每一个内角是( )
A.120° B.108° C.90° D.60
5.如果一个正多边形的一个内角与一个外角的度数之比是7:2,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
6.如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.260° C.270° D.360°
二.填空题
7.已知正n边形的每个内角为144°,则n= .
8.已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为 .
9.如图所示,正五边形中∠α的度数为 .
10.为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是 度.
11.如图,已知∠B=30°,则∠A+∠D+∠C+∠G= °.
12.如图,将△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A'的位置,若∠A=40°,则∠1﹣∠2的度数为 度.
三.解答题
13.一个多边形的每个内角都相等,都等于150°,求这个多边形的边数?
14.在四边形ABCD中,∠D=60°,∠B=∠A+20°,∠C=2∠A,求∠B的度数.
15.如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=70°,∠ACB=40°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
16.(1)已知图①中的三角形ABC,分别作AB,BC,CA的延长线BD,CE,AF,测量∠CBD,∠ACE,∠BAF的度数,并计算∠CBD+∠ACE+∠BAF.由此你有什么发现?请利用所学知识解释说明;
(2)类似地,已知图②中的四边形PQRS,分别作PQ,QR,RS,SP的延长线QG,RH,SM,PN,测量∠RQG,∠SRH,∠PSM,∠QPN的度数,并计算∠RQG+∠SRH+∠PSM+∠QPN.由此你又有什么发现?
(3)综合(1)(2)的发现,你还能进一步得到什么猜想?
参考答案
一.选择题
1.解:∵AB∥CD,
∴∠C+∠B=180°,
∵五边形ABCDE中,∠A=135°,∠D=150°,
∴∠E=540°﹣180°﹣135°﹣150°=75°.
故选:D.
2.解:A、三角形的一个外角大于与它不相邻的任何一个内角,故原说法错误,故本选项符合题意;
B、边数为n的多边形内角和是(n﹣2)×180°,说法正确,故本选项不合题意;
C、有一个内角是直角的三角形是直角三角形,说法正确,故本选项不合题意;
D、角形的中线、角平分线、高线都是线段,说法正确,故本选项不合题意;
故选:A.
3.解:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数==10,
∴这个正多边形的边数是10.
故选:B.
4.解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5.
则这个正多边形的每一个内角为540°÷5=108°.
故选:B.
5.解:设这个正多边形的边数为n,
由题意得:(n﹣2)×180=360,
解得:n=9,
故选:C.
6.解:如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故选:A.
二.填空题
7.解:由题意得正n边形的每一个外角为180°﹣144°=36°,
n=360°÷36°=10,
故答案为10.
8.解:设这个多边形的边数为n,依题意得:
(n﹣2)180°=×360°,
解得n=5.
故这个多边形的边数为5.
故答案为:5.
9.解:∵正五边形的内角为:(5﹣2)×180°÷5=108°,
∴∠α=×(180°﹣108°)=36°,
故答案为:36°.
10.解:如图,
∵正五角星中,五边形FGHMN是正五边形,
∴∠GFN=∠FNM==108°,
∴∠AFN=∠ANF=180°﹣∠GFN=180°﹣108°=72°,
∴∠A=180°﹣∠AFN﹣∠ANF=180°﹣72°﹣72°=36°.
故答案是:36.
11.解:∵∠B=30°,
∴∠BEF+∠BFE=180°﹣30°=150°,
∴∠DEF+∠GFE=360°﹣150°=210°.
∵∠DEF=∠A+∠D,∠GFE=∠C+∠G,
∴∠A+∠D+∠C+∠G=∠DEF+∠GFE=210°,
故答案为:210.
12.解:如下图所示,
∵△ABC纸片沿DE进行折叠,点A落在四边形BCED的外部点A'的位置,
∴∠4=∠5,∠3=∠2+∠DEC,
∵∠1+∠4+∠5=180°,
∴∠1+2∠4=180°,
∴∠1=180°﹣2∠4,
∵∠3+∠DEC=180°,
∴∠2=∠3﹣∠DEC=2∠3﹣180°,
∴∠1﹣∠2=180°﹣2∠4﹣2∠3+180°=360°﹣2∠4﹣2∠3=2∠A,
∴∠1﹣∠2=2×40°=80°,
故答案为:80.
三.解答题
13.解:由题意可得:180°?(n﹣2)=150°?n,
解得n=12.
故多边形是12边形.边数为12.
14.解:四边形内角和定理得:∠A+∠B+∠C+∠D=360°,
∵∠D=60°,∠B=∠A+20°,∠C=2∠A,
∴∠A+(∠A+20°)+2∠A+60°=360°,
∴∠A=70°,
∴∠B=∠A+20°=90°,
答:∠B的度数是90°.
15.解:(1)∵∠ACE=∠A+∠ABC,
∴∠ACD+∠DCE=∠A+∠ABD+∠DBC,∠DCE=∠D+∠DBC,
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE﹣∠DBC),∠D=∠DCE﹣∠DBC,
∴∠A=2∠D,
∵∠ABC=70°,∠ACB=40°,
∴∠A=180°﹣∠ABC﹣∠ACB=70°,
∴∠D=35°;
(2)∠D=(∠M+∠N﹣180°);
理由:延长BM、CN交于点A,
∵∠A+∠ANM+∠AMN=180°,∠AMN+∠BMN=180°,∠ANM+∠CNM=180°,
∴∠A=180°﹣∠ANM﹣∠AMN=180°﹣(180°﹣∠CNM)﹣(180°﹣∠BMN)=180°﹣180°+∠CNM﹣180°+∠BMN,
则∠A=∠BMN+∠CNM﹣180°,
由(1)知,∠D=∠A,
∴∠D=(∠BMN+∠CNM﹣180°).
16.解:(1)
∠CBD=138°,∠ACE=117°,∠BAF=105°,
所以∠CBD+∠ACE+∠BAF=360°,
发现:三角形中的外角和为360°,
理由:因为∠CBD+∠ABC=180°,
∠ACE+∠ACB=180°,
∠BAC+∠BAF=180°,
所以∠CBD+∠ACE+∠BAF+∠ABC+∠ACB+∠BAC=540°,
又因为∠ABC+∠ACB+∠BAC=180°,
所以∠CBD+∠ACE+∠BAF=360°;
(2)
∠RQG=125°,∠SRH=113°,∠PSM=48°,∠QPN=74°,
所以∠RQG+∠SRH+∠PSM+∠QPN=360°;
发现:在四边形的外角和是360°;
∵∠RQG+∠PQR=180°,∠SRH+∠QRS=180°,∠PSM+∠RSP=180°,∠QPN+∠QPS=180°,
∵∠RQG+∠PQR+∠SRH+∠QRS+∠PSM+∠RSP+∠QPN+∠QPS=720°,
∵∠PQR+∠QRS+∠RSP+∠QPS=360°,
∴∠RQG+∠SRH+∠PSM+∠QPN=360°.
(3)猜想:多边形的外角和和都是360°.
设多边形为n边形,则n边形的每一个内角与它相邻的外角的和为180°,
∴n边形的外角和=180°n﹣(n﹣2)×180°=180°n﹣180°n+360°=360°.
